一种快速求解宽频简正波的方法
2018-04-11朱飞龙李风华EricThorsos
朱飞龙,李风华,Eric I. Thorsos
一种快速求解宽频简正波的方法
朱飞龙1,2,李风华1,Eric I. Thorsos3
(1. 中国科学院声学研究所声场声信息国家重点实验室,北京 100190;2. 中国科学院大学,北京 100049;3.Applied Physics Laboratory, University of Washington WA, 98105 USA)
针对宽带信号的简正波解,传统的求解简正波数值方法常常需要重复计算本征值方程,计算效率低。文中将频率的变化当作扰动,提出利用微扰理论得到参考频率附近的简正波解。该方法具有直接、精确、高效的特点,计算得到的水平波数和本征函数与KRAKENC程序计算结果吻合较好,两种方法计算得到的脉冲波形最大相关系数大于0.97。
微扰理论;简正波;宽带信号;脉冲波形
0 引言
简正波方法在水声学中有着广泛的应用。自从Pekeris最早于1948年发表了关于简正波的理论[1]后,简正波方法取得了长足的发展。简正波方法的最初应用,就是准确求解本地简正波的本征值和本征函数。除了少数理想的波导可以得到简正波的解析解外,大部分实际应用都需要借助现有程序得到简正波的数值解。现在得到广泛应用的求解简正波的程序有KRAKEN[2],适用于深海环境的广义相积分简正波[3]和适用浅海环境的波束位移射线简正波(Beam Displacement Ray Mode,BDRM)[4]方法也可以快速地得到简正波解。
在考虑宽频信号的时候,比如1/3倍频程带宽,上述传统的程序需要多次重复计算简正波的本征方程,计算效率低。为此针对吸收性波导环境,王宁等[2]提出了哈密顿方法,通过降低本征值搜索维度,一定程度上提高了简正波的求解速度,并将该方法应用到求解宽频信号的简正波[6]。很多学者提出了间接求解宽频简正波的方法。Robert等[7]通过对本征函数进行分解,在参考频率的简正波已知时,利用盖勒金方法得到宽带信号简正波的近似解,但是该方法的精度不高。王宁等[8]将本征值问题转化成动态系统问题,通过矩阵运算,直接得到了参考频率附近频率的简正波解。Tindle等[9]针对海水声速剖面水平变化的环境,利用微扰理论直接得到了本地简正波解。本文提出一种由微扰理论直接得到宽带信号简正波解的方法。
1 微扰简正波理论
在水平不变波导环境下,分层介质中假定各层内的密度是常数,此时深度分离的本征值方程[10]

在有限海深环境下,本征值方程式(1)有无穷多个离散解。当波导环境不存在吸收时,本征值和本征函数都是实数,并且本征函数相互正交,构成一个完备集[11]。当海底存在吸收时,本征值和本征函数是复数,此时本征函数满足不含复共轭的双正交归一性(Bi-orthogonality)[12-13],即



新的简正波同样要满足本征方程,将新的参数值代入式(1)中,忽略二阶微扰项,化简后得到本征水平波数变化量为

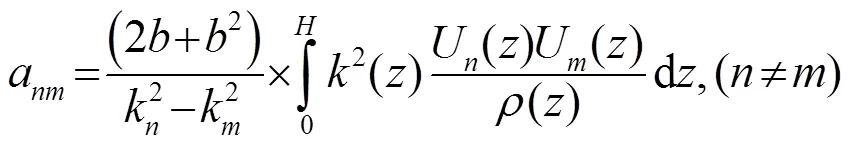

2 浅海波导环境
建立如表1所示的浅海水平不变波导,为了计算方便,在基底厚度50 m处人为加入真空层。参考简正波的本征值和本征函数由KRAKENC方法计算得到,对应的参考频率为中心频率800 Hz。声场计算中的简正波号数为30,其中包含25号波导模式简正波。在微扰法计算中使用的简正波号数为40。
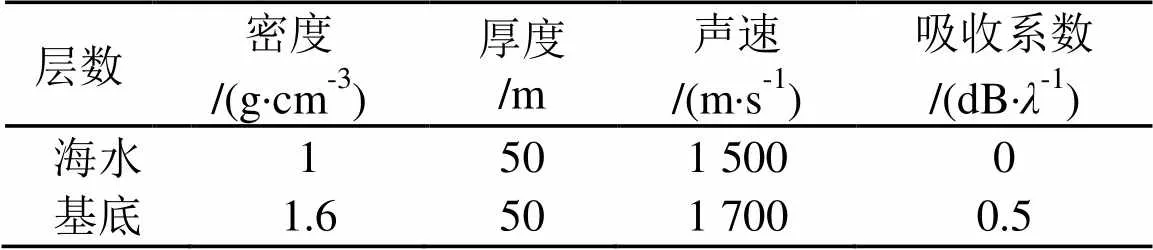
表1 浅海波导环境参数
2.1 单频验证

注意到在图1中,频率850 Hz时本征水平波数的误差比750 Hz时的误差大。主要是因为随着频率增加,前40号简正波内正则模式简正波(波导模式和耗散模式简正波)[14]数量也会增加,增加的简正波来自于更高号的耗散模式简正波。但是微扰法得到的简正波正则模式和连续模式数量不变,所以会导致高号简正波特别是高号正则模式简正波的误差较大。
相反,当频率减小时,前40号简正波内正则模式简正波数量减少,而微扰法保持了正则模式简正波的数量,所以依然能得到相对较高精度的本地简正波。因此增加简正波的号数,以及适时插入本地真实的简正波可以提高计算精度。
图2给出了在频率850 Hz下,本文方法与KRAKENC方法计算得到的第10号简正波本征函数值的对比。从图2中看出,微扰法近似结果与KRAKENC方法计算得到的结果吻合很好。
综上结果可知,本文提出的微扰法得到的简正波解与KRAKENC方法直接计算得到的结果吻合较好,精度较高。此外,在MATLAB程序中,本文方法计算一次简正波的时间约为0.47 s;而在相同环境下,KRAKENC方法计算一次简正波时间为57.35 s,是本文方法的100倍,可见本文方法计算效率很高。
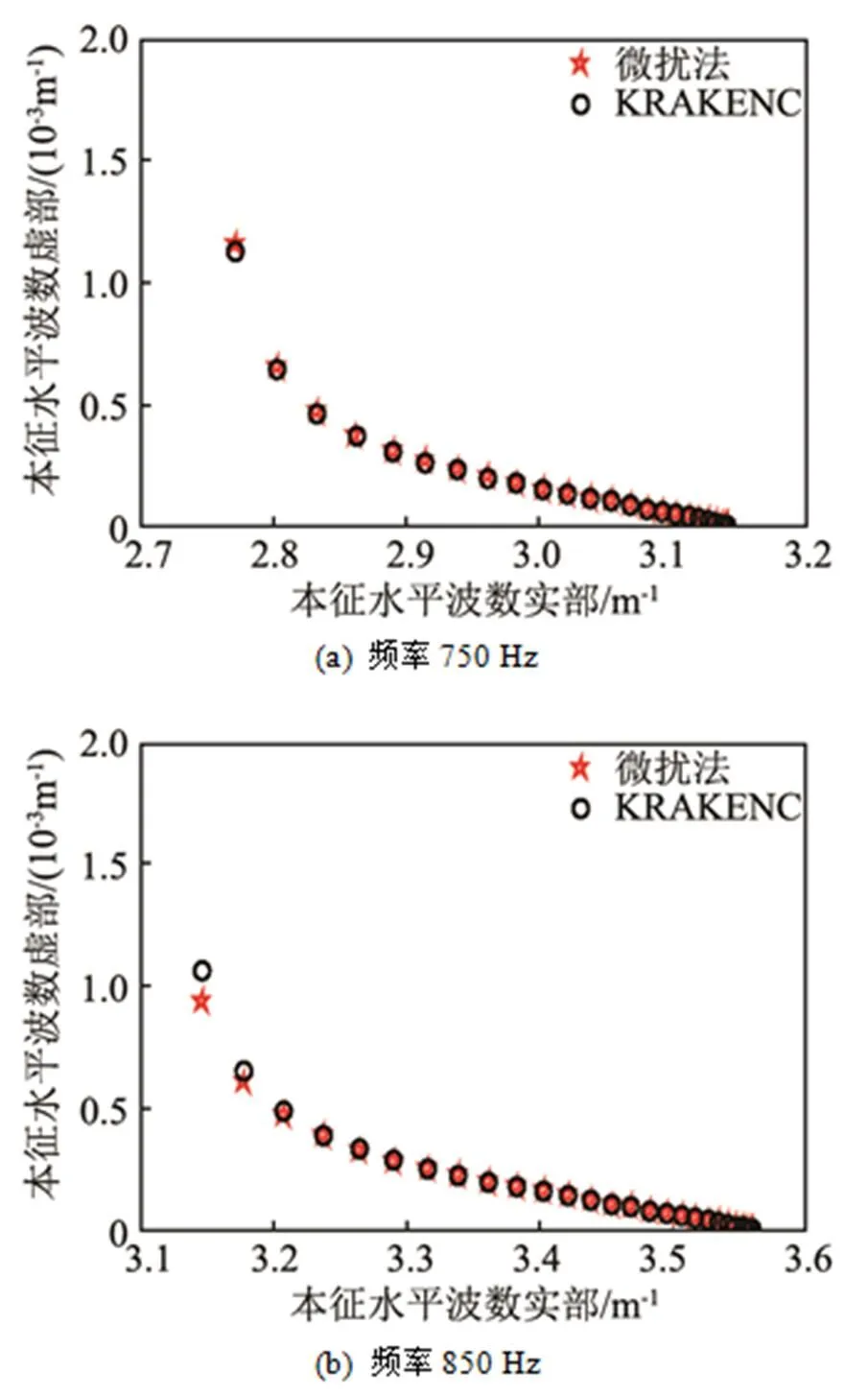
图1 水平波数估计值与KRAKENC方法计算结果对比,参考频率800 Hz
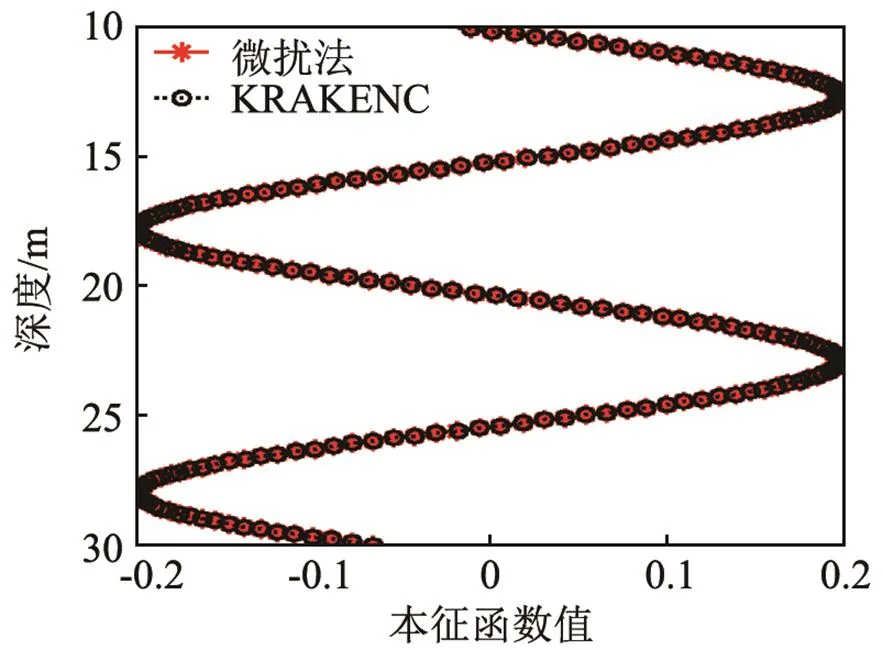
图2 频率850 Hz下,第10号简正波本征函数值对比,参考频率800 Hz
2.2 脉冲波形

从图3看出,两种方法结果吻合很好。根据波形相关系数公式

其中:是由微扰法得到的时域波形;是由KRAKENC方法计算得到的时域波形;T是逆傅里叶变换得到的时域波形周期。计算得到两种方法的波形相关系数,显然结果是非常精确的。其中本文方法所用时间为98.16 s,KRAKENC方法计算结果所用时间为6 805 s,是本文方法的70倍。
3 深海环境验证
建立深海水平不变波导环境,海水深度为4 000 m,一次实测的海水声速剖面如图4所示。海底参数如表2所示,为了计算方便,在基底厚度505 m处人为地加入了真空层。参考中心频率为100 Hz,声场计算中包含了150号简正波,用于微扰法计算的简正波号数为200。

图4 海水声速剖面
位于200 m深度的脉冲声源,中心频率为100 Hz,带宽为20 Hz。图5给出了在距离60 km、接收深度1 000 m处,由本文方法得到的时域波形与KRAKENC方法计算结果的对比。从图5中看出,两种方法的波形结果吻合较好,并且两个时域波形的最大互相关系数约为0.91。当只取峰值到达附近的波包时,两种结果的波形最大互相关系数可以达到0.972,这样的精度可以满足大部分声场计算的需求。此外,在深海环境下,本文一次简正波计算时间为2.4 s,而KRAKENC方法计算时间则约为76.4 s,是本文方法的30倍。

表2 深海海底参数

图5 接收时域波形,声源深度200 m,中心频率100 Hz,带宽20 Hz,接收距离60 km,接收深度1 000 m
4 结论
本文利用微扰理论,提出了一种快速求解宽带信号简正波的方法。本文方法有以下优点:
(1) 可以直接得到参考频率附近简正波的本征值和本征函数,适用于深海和浅海波导环境,应用范围广;
(2) 计算速度快,一次简正波的计算时间比KRAKENC方法快30倍以上;
(3) 计算精度较高,本文方法得到的简正波水平波数和本征函数与KRAKENC方法计算结果吻合较好,在浅海环境下得到的时域脉冲波形与KRAKENC方法计算结果最大相关系数为0.99,在深海环境下,峰值所在的波包最大相关系数大于0.97。
[1] PEKERIS C L. Theory of propagation of explosive sound in shallow water[J]. Geol. Soc. Am. Mem, 1948, 27: 1.
[2] PORTER M B. The KRAKEN Normal Mode Program. 2009. http://oalib.hlsresearch.com/Modes/AcousticsToolbox/manualtml/kraken. html.
[3] 张仁和, 何怡, 刘红. 水平不变海洋声道中的 WKBZ 简正波方法[J]. 声学学报, 1994, 19(1): 1-12. ZHANG Renhe, HE Yi, LIU Hong. WKBZ mode approach to sound propagation in horizontally stratified oceans[J]. Acta Acustica, 1994, 19(1): 1-12.
[4] ZHANG Renhe, LI Fenghua. Beam-displacement ray-mode theory of sound propagation in shallow water[J]. Science in China(Series A), 1999, 42(7): 739-749.
[5] WANG N, WANG H Z. A Hamiltonian solver for finding modal eigenvalues[J]. J. Comput. Acoust., 2010, 18(3): 259-266.
[6] WANG Haozhong, WANG Ning, GAO Dazhi. A Hamiltonian method for finding broadband modal eigenvalues[J]. J. Acoust. Soc. Am., 2012, 131(2): 1047-1054.
[7] ROBERT A K, KNOBLES D P. A practical application of the Galerkin method to the broadband calculation of normal modes for underwater acoustics[J]. J. Acoust. Soc. Am., 1995, 98(3): 1682- 1698.
[8] WANG Ning, LIU Jin zhong. New approach to the normal mode method in underwater acoustics[J]. Chinese Physics, 2002, 11(5): 456-460.
[9] TINDLE C T, O’ DRISCOLL L M, HIGHAM C J. Coupled mode perturbation theory of range dependence[J]. J. Acoust. Soc. Am., 2000, 108(1): 76-83.
[10] JENSEN F B, KUPERMAN W A, PORTER M B, et al. Computational ocean acoustics[M]. 2ndedition. New York: Springer, 2011.
[11] WILCOX C H. Sound Propagation in stratified fluids[M]. New York: Springer, 1984, Chaper 2, Section 1: 13-17, Chaper 3, Section 9: 104-116.
[12] FRIEDMAN B. Principles and techniques of applied mathematics [M]. New York: Wiley, 1956: Chapter 4.
[13] WAXLER R. A vertical eigenfunction expansion for the propagation of sound in a downward-refracting atmosphere over a complex impedance plane[J]. J. Acoust. Soc. Am., 2002, 112(6): 2540-2552.
[14] BUCKINGHAM M J, GIDDENS E M. On the acoustic field in a Pekeris waveguide with attenuation in the bottom half-space[J]. J. Acoust. Soc. Am., 2006, 119(1): 123-142.
A fast method for broadband normal mode computation
ZHU Fei-long1,2, LI Feng-hua1, Eric I. Thorsos3
(1. State Key Laboratory of Acoustics, Institute of Acoustics, Chinese Academy of Sciences, Beijing 100190, China;2. University of Chinese Academy of Sciences, Beijing 100049, China;3. Applied Physics Laboratory, University of Washington WA, 98105, USA)
For the broadband normal mode computation, conventional normal mode numerical code needs to be used repeatedly, which lowers the computational efficient. Viewing the change of frequency as perturbation, a fast method based on perturbation theory is presented in this paper. This method is direct, fast and accurate. Numerical simulations in shallow water and deep ocean are performed, the calculated horizontal wave-numbers and modal eigen-functions by this method agreewell with those obtained by KRAKENC method, and the maximum cross correlation between the impulse waveforms calculated by thetwo methods is greater than 0.97.
perturbation theory; normal mode; broadband signal; impulse waveform
O427
A
1000-3630(2018)-01-0038-05
10.16300/j.cnki.1000-3630.2018.01.007
2017-04-21;
2017-06-19
国家自然科学基金资助项目(11125420)
朱飞龙(1989-), 男, 江西赣州人, 博士研究生, 研究方向为水声物理。
李风华, E-mail: lfh@mail.ioa.ac.cn
