去中心化时差频差直接定位方法

朱颖童， 董春曦， 董阳阳， 许锦， 赵国庆

西安电子科技大学 电子信息攻防对抗与仿真技术教育部重点实验室， 西安 710071

去中心化时差频差直接定位方法

朱颖童*， 董春曦， 董阳阳， 许锦， 赵国庆

西安电子科技大学 电子信息攻防对抗与仿真技术教育部重点实验室， 西安 710071

针对原始利用时差频差的直接定位(DPD)方法存在数据传输量和计算量大的瓶颈，提出了两种去中心化直接定位方法。第1种方法采用去中心化配对方案，只将各观测站截获信号在站间进行一次传输，将数据传输和计算分散到各观测站间并行计算互模糊函数(CAF)，构造仅满足满秩条件的互模糊矩阵(CAM)。第2种方法根据推导的任意互模糊函数间关系公式，采用归约方式去中心化的在各观测站并行计算余下互模糊函数，补全互模糊矩阵。两种方法都降低了直接定位数据传输量，提高了计算效率。性能分析和仿真实验表明本文两种方法精度性能优于两步定位方法，在低信噪比时两种方法都可达到比较理想的精度性能，在高信噪比时第2种方法与原始直接定位方法的精度性能相当。

直接定位； 无源定位； 互模糊函数； 去中心化； 观测站配对； 克拉美罗下界

无源定位具有作用距离远，安全隐蔽性能好等优势，是电子对抗的一个重要的研究方向[1]。无源定位已广泛应用于飞机、卫星、无线传感器网络等平台。近年来将无源定位应用于低成本无人机蜂群(LOw-Cost UAV Swarm Technology，LOCUST)这类自组协同受尺寸、重量、功率、成本(Size Weight and Power Cost，SWaP-C)[2]约束的分布式平台，对定位算法提出了更苛刻的要求。无源定位一般采用两步定位方法，首先利用截获信号估计到达角(Direction Of Arrival，DOA)、到达时间(Time Of Arrival，TOA)、时差(Time Difference Of Arrival，TDOA)、频差(Frequency Difference Of Arrival，FDOA)和信号强度(Received Signal Strength，RSS)等参数，再利用这些参数估计辐射源位置。

Wax和Kailath[3]首先提出了直接利用多个阵列的信号采样，计算协方差矩阵实现窄带辐射源数目及位置的一步估计，并讨论了位置与频率联合估计以及运动辐射源的情况。Weiss等[4-7]将直接利用信号实现辐射源位置一步估计的方法命名为直接定位(Direct Position Determination，DPD)方法。这类方法避免了两步方法所需的信号分选和参数配对过程，且可在低信噪比下得到精度更高的定位结果。Oispuu和Nickel[8]首先提出运动单站天线阵列对多个间歇辐射的辐射源目标的检测和直接定位方法。郭福成等[9-10]提出利用运动单站干涉仪接收的信号数据估计辐射源位置的直接定位方法，采用一组干涉仪便可对多个频段辐射源进行定位，且在低信噪比下优于多通道干涉仪仅测角和长基线相位差变化率定位方法。王鼎等[11]也采用运动单站天线阵，依据相位调制信号具有的恒包络特性，根据最大似然准则实现辐射源的直接定位，明显提高了位置估计的精度。Bosse等[12]提出Global MUSIC方法实现多站天线阵对多个辐射源目标的直接定位。黄志英等[13]在实现多站天线阵对多个辐射源直接定位时考虑阵列的非一致噪声，通过交替迭代的方式对噪声协方差矩阵以及目标位置进行联合估计。

Weiss等在文献[6-7]中分别提出了多个观测站对单个固定辐射源的直接定位方法，每个观测站只有一个接收机截获一路信号，基于时差或频差或两者联合,分别适用于窄带和宽带的未知或先验已知信号。Kay等[14-15]利用多个观测站实现辐射源的低截获(Low Probability of Intercept，LPI)信号检测和直接定位，针对采样信号存在的信号量化效应影响定位性能，采用了连续时间信号模型，适用于窄带、宽度、低通和高通的辐射时间未知的未知或已知信号。直接定位方法由于利用信号进行定位，因此存在着数据传输量大、计算量大等瓶颈。

为了克服这些瓶颈，Fowler等在文献[2]和文献[16-17]中分别提出了数据压缩和分布式计算的方法，并分析了其对直接定位精度性能的影响。王云龙和吴瑛[18]利用矩阵转置后的非零特征值相同这一性质，降低代价函数中矩阵的维数，减小其特征值分解的计算量。夏威等[19-20]提出自适应分布式计算实现辐射源直接定位，将各观测站截获采样的信号传输给邻近观测站而非单一观测站或者融合中心(Fusion Center)，显著降低了数据通信量且将计算量分散到各观测站。另外采用最速下降的迭代方式，不需要遍历计算所有格点，降低了估计辐射源位置所需的总计算量。

相关基于时差或频差或两者联合的直接定位，需将L个观测站两两配对成共L(L-1)/2组配对，将各站截获信号两两配对逐一计算广义互相关(Generalized Cross Correlation，GCC )[21]或者互模糊函数(Cross Ambiguity Function，CAF)[22]，每个网格点再构造包含辐射源位置信息的Hermite矩阵的L(L-1)/2个矩阵元素。Hermite矩阵即为互模糊矩阵(Cross Ambiguity Matrix，CAM)。而两步定位法只利用L-1组配对，提取L-1组时差和频差用于定位解算。另外在两步定位方法中，由于中间变量包含有辐射源与某一观测站之间的斜距，需要设定主观测站和副观测站，所用参数一般为主副观测站间的时差或频差。定义主副观测站间的时差和频差为中心化时差和频差。

由于各观测站截获的是相同辐射源同一时刻的信号，GCC或CAF间满足相应关系。因此，提取L-1组时差频差，只计算L-1个GCC或CAF，其他(L-1)(L-2)/2个函数不需计算GCC或CAF，可利用函数间关系公式产生，以补全互模糊矩阵，极大降低了观测站间数据传输量和计算量。

综上，本文尝试提出两种方法构造互模糊矩阵，第1种方法不需全部计算L(L-1)/2个矩阵元素，只需要满足矩阵满秩的条件，最少只需要计算L-1个矩阵元素，降低计算量。与文献[2，19-20]类似，不设定主观测站或者融合中心，采用去中心化的观测站配对方案，观测站只向邻近的观测站转发截获信号，极大降低了定位系统的数据传输量。采用分布式的计算方式，将原来相关运算都在同一个观测站的方式改为分散到各个观测站分别计算，缩减了定位计算所消耗的总时间。第2种方法在第1种方法计算得到的L-1个GCC或CAF基础之上，利用函数之间的关系计算余下(L-1)(L-2)/2个GCC或CAF，在保证构造出所有矩阵元素的情况下，极大降低了数据传输量和计算量。

由于时差频差联合的直接定位可简化得到时差或频差的直接定位，因此本文讨论时差频差联合的直接定位。本文内容组织如下：第1节给出模型并总结相关直接定位方法，第2节给出两种互模糊矩阵构造方法，第3节推导各定位方法克拉美罗下界(Cramer-Rao Lower Bound，CRLB)，第4节进行仿真实验，第5节给出结论。

1 问题模型

假设辐射源目标位置为p。L个观测站的位置和速度分别为pl和vl，l=1,2,…,L。各观测站K个时间段T内截获的辐射源信号表示为

rl,k(t)=bl,ksk(t-tl,k)ej2πfl,kt+wl,k(t)

0≤t≤T

(1)

式中：k=1,2,…,K；bl,k为信号辐射到达观测站l的传播损耗；sk(t)为信号波形；wl,k(t)为零均值加性高斯白噪声；T为观测时间；tl,k和fl,k分别为第k时间段内信号到达观测站l的到达时间和多普勒频移，其表达式分别为

(2)

(3)

信号到达观测站l和m的时差和频差分别为

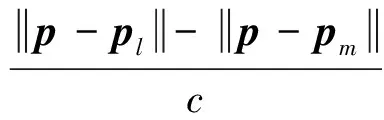
(4)

flm,k=fl,k-fm,k=

(5)

为了讨论的简便，假定在观测时间内满足τlm,k≪T，即定位过程中时差和频差保持不变。

文献[16-17]指出对截获的信号进行采样和压缩传输会产生量化误差，文献[15]指出观测站间的同步误差影响估计结果，文献[23]指出运动观测站间截获信号的转发传播误差影响估计结果。

文献[2,6,14,19-20]对各观测站截获信号时域直接采样，采样率限制了时差的量化精度。文献[16-17]将信号进行离散傅里叶变换、小波包变换和短时傅里叶变换后再量化压缩，压缩时在时差频差精度，计算量与传输量之间取舍。文献[8，15，18]将信号用傅里叶系数表示，对于带限信号，可以只保留有限个非零系数来近似信号。因此，在这里将截获信号用傅里叶系数表示，同时考虑量化和同步等误差。

(6)

可以将式(6)写成如下向量形式：

(7)

式中：

Dl,k=diag(e-j2πf-Ntl,k,e-j2πf-N+1tl,k,…,e-j2πfNtl,k)

综合相关文献给出辐射源位置直接估计方法的步骤如下。将所有观测站截获得到的辐射源信号集中传输到同一位置，如主观测站。对于每一个网格点pg，g=1,2,…,G，计算信号从该网格点传播到各观测站的传播时间和多普勒频率，构造如下包含位置信息的矩阵:

(8)

式中：矩阵Dl和Fl对应着网格点传播到各观测站的传播时间和多普勒频率。

对于任意给定的矩阵X，由于XHX与XXH非零特征值相同。因此，构造L×L矩阵：

(9)

将所有时间段该矩阵最大特征值相加，将各网格点对应值组成集合，集合中的最大值对应的网格点即为辐射源估计位置。可写成

(10)

矩阵Qpg,k为互模糊矩阵。Qpg,k对角线上的第l个元素为观测站l在第k时间段内截获信号的能量。Qpg,k的第(l,m)个非对角线元素是观测站l和m在第k个时间段内截获信号的互模糊函数。

(11)

式中：τg和fg分别为观测站l和m相对于网格点pg所对应的时差和多普勒频差。

2 去中心化直接定位方法

相关直接定位方法构造互模糊矩阵Qpg,k用于特征值求解以估计辐射源位置，都需要计算出所有矩阵元素。由于互模糊矩阵是Hermite矩阵，因此对于每个观测时间段都需要计算L(L-1)/2个互模糊函数和L个截获信号能量。相关直接定位方法需将各观测站截获信号转发到主观测站，再针对每个网格点将所有观测站截获信号构造成数据矩阵以构造互模糊矩阵。

2.1 去中心化构造仅满秩互模糊矩阵

两步定位方法利用观测站截获信号测量的时差频差进行定位解算时，一般只利用了L-1组时差频差。而将L个观测站两两配对，最多可以有LL-1/2组配对，计算LL-1/2个互模糊函数，测量得到LL-1/2组时差频差。直接定位方法构造互模糊矩阵Qpg,k时利用了全部LL-1/2 组配对，而两步定位方法一般只利用其中L-1组实现定位解算。直接定位法构造的互模糊矩阵Qpg,k如果也只利用L-1组配对，计算L-1个互模糊函数构造仅满秩的互模糊矩阵，不构造所有矩阵元素，此时互模糊矩阵刚好满足满秩条件，可求解特征值以估计辐射源位置。构造仅满秩的互模糊矩阵可降低定位系统的计算量。

根据文献[24]的思路，将时差频差用变换矩阵乘以到达时间和到达频率向量进行表示。令τd=Tτ和fd=Tf分别表示定位中涉及到的时差和频差向量。其中:τ=[τ1τ2…τL]T和f=[f1f2…fL]T分别为L个观测站截获的信号到达时间向量和到达频率向量；T为列数为L的变换矩阵，T的行数可以为L-1至L(L-1)/2的任意值，T的每行只有一个1和-1。

两步定位方法提取L-1个时差频差需设定主观测站，其他L-1个观测站为副观测站，将主副观测站配对，各副观测站截获信号转发到主观测站计算互模糊函数，提取中心化时差频差。不失一般性假定观测站1为主观测站，中心化时差向量和频差向量分别为τdC=[τ21τ31…τL1]T和fdC=[f21f31…fL1]T。中心化变换矩阵为

(12)

根据文献[25]，与观测站l配对的观测站集合用Nl表示，与观测站l配对的观测站数目称为观测站l的度(degree)，用Dl表示。Dl的数值即对应着互模糊矩阵第l行和第l列中非零元素的数目。两步定位法的中心化配对方案主观测站的度D1=L，副观测站的度Dl=2。

中心化配对方案计算构造的仅满足满秩条件的互模糊矩阵中各非对角线非零元素分别对应不同观测站配对的互模糊函数，对角线元素为各观测站截获信号的能量。具体形式为

(13)

式中：All为观测站l截获信号的能量；Clm为观测站l和m对应网格点pg的互模糊函数数值。

中心化时差频差的互模糊函数计算和提取需将数据传输和计算都集中于单一观测站或者融合中心，限制了定位的数据传输和计算效率以及观测站网络扩展。由于直接定位方法无需满足中心化限制，可采用去中心化的观测站配对方案，不设定主观测站，各观测站只向邻近站转发截获信号，在各观测站并行计算L-1个互模糊函数，提高直接定位的数据传输和计算效率，便于观测站网络扩展。

由于观测站间的基线长度影响定位性能，为了利用有限的L-1个互模糊函数尽可能地提高定位精度，可以使观测站配对间总距离尽可能大。

(14)

目标函数式(14)得到的最优观测站标号排列Sn使得观测站配对间总距离最大。将Sn中观测站标号排列依次序替换为1到L。采用去中心化配对观测站方案，将替换标号后的观测站l和l+1 进行配对，并行地将观测站l+1截获信号只转发至邻近观测站l。此时各观测站的度相同，都是Dl=3。采用分布式计算，将原来互模糊函数计算集中于单一观测站或融合中心的方式改为分散到各观测站并行计算，缩减计算所有互模糊函数所需时间。

去中心化观测站配对方案对应去中心化时差和频差向量分别为τdD=[τ21τ32…τL(L-1)]T和fdD=[f21f32…fL(L-1)]T，去中心化变换矩阵为[26]

(15)

采用去中心化配对方案计算互模糊函数构造的互模糊矩阵的具体形式为

(16)

式中：All与Clm的意义与式(13)相同。

综上，给出去中心化构造仅满足满秩条件的互模糊矩阵，实现直接定位的步骤如下：

步骤1根据观测站位置的拓扑结构，按照目标函数式(14)得到各观测站的最优标号集合。

步骤2在各观测站计算第k时间段内截获信号的能量El,k。

步骤3在第k时间段，任意观测站l+1将截获信号转发至观测站l，其中l=1,2，…,L-1。

步骤4在观测站l计算CAFl(l+1),k，并将相应的时差频差的互模糊函数数值与对应的网格点pg关联，得到[CAFl(l+1),k]pg。

步骤5对于每一个网格点pg，构造形如式(16)的互模糊矩阵Qpg,k，其中第l个对角线元素为El,k，第l行l+1列与第l+1行l列非对角元素分别为[CAFl(l+1),k]pg与其共轭。

步骤6计算该时间段内互模糊矩阵Qpg,k的最大特征值λmax(Qpg,k)。

2.2 去中心化补全互模糊矩阵

根据2.1节构造的互模糊矩阵估计辐射源位置，虽然极大地提高了数据传输和计算的效率，但因为没有充分利用所有的观测站配对以计算互模糊矩阵的所有元素，因此无法达到原始直接定位方法的精度性能，在低信噪比下得到精度较高的定位结果。文献[2]在提出的HC直接定位方法中给出了主副站间的互模糊函数关系公式。本节将该关系公式推广，采用2.1节利用信号计算L-1个去中心化互模糊函数后，再去中心化的在各观测站并行计算余下的互模糊函数，补全互模糊矩阵所有元素。

由于观测站间需多次数据传输，为了降低观测站间的数据传输时延，需要观测站配对间总距离尽可能小。

因此，根据目标函数式(14)中各符号的定义，以及各观测站位置构造如下目标函数：

(17)

目标函数式(17)得到的最优观测站标号排列Sr使得观测站配对间总距离最小。将Sn中的观测站标号排列依次序替换为1到L。

因为变换矩阵T秩为L-1，而τmn=τln-τlm和fmn=fln-flm，因此在所有L(L-1)/2个时差频差中，获得其中包含所有观测站数据的L-1个时差频差，其他时差频差都可以由L-1个时差频差组成的向量经过初等变换计算得到[24]。

由于各观测站截获的是相同辐射源同一时刻的信号，在所有L(L-1)/2个互模糊函数中，计算出其中L-1个包含所有观测站数据的互模糊函数，其他互模糊函数都可以由L-1个互模糊函数计算得到。下面将文献[2]的关系公式推广到任意观测站配对的情况。第k时间段观测站l截获的不含噪声信号为

(18)

式(18)即式(1)不含噪声的形式。相同时间段内观测站m截获信号与式(18)的关系为

(19)

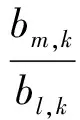
因此，两者的互模糊函数可表示为

CAFlm,k(τ,f)=

G*ej2πflm,kτAAFl,k(τ-τlm,k,f-flm,k)

(20)

式中：

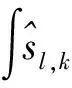
(21)

由式(21)可得

(22)

式中：AAFl,k(0,0)为观测站l截获信号的能量El,k。

任意观测站m与n的互模糊函数可用任意观测站l与n的互模糊函数表示，表达式为

CAFmn,k(τ,f)=

Gej2πfτlm,kCAFln,k(τ+τlm,k,f+flm,k)

(23)

将式(22)代入式(23)可得互模糊函数之间关系公式。

CAFmn,k(τ,f)=

(24)

利用式(24)任意互模糊函数间的关系公式，可采用归约方式在各观测站并行计算余下互模糊函数，补全互模糊矩阵，降低时间复杂度。根据文献[27]，归约(Reduction)是将位于不同观测站的多个结果综合起来，通过某些操作或计算产生新的结果，存储在指定的观测站。采用归约的方式在各观测站并行计算互模糊函数，共需计算L-2次循环。循环之前将观测站l+1计算的信号能量El+1,k传递到观测站l。在第i次循环中，观测站l+1将上次循环计算得到CAF(l+1)(l+i+1),k传递到观测站l，根据互模糊函数之间关系公式(24)，在观测站l处与CAFl(l+1),k和El+1,k计算得到CAFl(l+i+1),k，再执行下次循环。第i次循环中l=1,2，…,L-i-1。

综上，基于L-1个去中心化互模糊函数，给出利用互模糊函数之间关系，采用归约的方式，补全互模糊矩阵，实现直接定位的步骤如下：

步骤1根据观测站位置的拓扑结构，按照目标函数式(17)得到各观测站的最优标号集合。

步骤2在各观测站l计算第k时间段内截获信号的能量El,k，并将其转发至观测站l-1。

步骤3和步骤4与2.1节中对应的步骤3和步骤4相同。

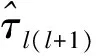
步骤6依次执行如下循环操作，在第i=1,2，…,L-2 次循环中，观测站l=1,2，…,L-i-1并行执行：

(1) 接收从观测站l+1传递的上次循环的计算结果CAF(l+1)(l+i+1),k。

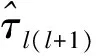
(3) 将相应的时差频差的CAFl(l+i+1),k数值与对应的网格点pg关联，得到[CAFl(l+i+1),k]pg。

步骤7对于每一个网格点pg，构造完整的互模糊矩阵Qpg,k，其中第l个对角线元素为El,k，第l行m列与第m行l列非对角元素分别为[CAFlm,k]pg与其共轭。

步骤8和步骤9与2.1节中步骤6和步骤7相同。

3 定位性能分析

下面分析比较定位方法的误差克拉美罗下界与计算复杂度。

3.1 定位误差克拉美罗下界

克拉美罗下界可以通过Fisher信息矩阵(Fisher Information Matrix, FIM)的逆求出[28]。为了分析的简便，对二维空间情况进行推导分析，三维空间的情况可以经过拓展得到。

文献[17]给出的观测站l截获信号经过变换和量化等之后传递到观测站m，任意时间段k内采用互模糊函数方法估计时差频差的FIM如下：

Jlm=2Re{GH[Σ+W]-1G}

(25)

式中：Σ为零均值加性高斯白噪声协方差；W为量化误差协方差；

(26)

为了便于分析，假定各观测站配对用互模糊函数方法估计的FIM相同，且满足：

(27)

式中：结合文献[6，22]有

(28)

(29)

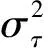
根据文献[17，26]，相关直接定位方法所有观测站两两配对计算互模糊函数构造互模糊矩阵的所有元素，辐射源位置估计的FIM为

(30)

式中：

(31)

当l≠m时，Tlm为变换矩阵T中某一行，该行的第l列为1，第m列为-1，其他都为零；当l=m时，行向量Tll中所有元素都为零。

将式(27)代入式(30)，整理得到FIM各元素为

(32)

同理，两步定位方法中采用中心化观测站配对方案，辐射源位置估计的FIM为

(33)

整理得到两步定位方法的FIM各元素为

(34)

2.1节计算L-1个互模糊函数去中心化的构造仅满秩互模糊矩阵的辐射源位置估计FIM如下：

(35)

整理得到该FIM各元素为

(36)

(37)

(38)

(39)

比较式(37)～式(39) 3个公式，相关直接定位方法各观测站配对都充分利用，FIM对角线上元素数值最大，因此位置估计的CRLB最小，精度性能最稳定。中心化配对方案的FIM非零元素集中在第1行和第1列，每个观测站配对都利用到主观测站与辐射源在空间中的相对位置、速度和截获信号等信息，位置估计CRLBC受主观测站影响较大，精度性能不稳定。去中心化的FIM非零元素均匀分布，均匀利用各观测站与辐射源在空间中相对位置、速度和截获信号，随着辐射源在空间中不同位置的变化，位置估计CRLBD具有较稳定的起伏，甚至可达到更高的位置估计精度。但与相关直接定位方法CRLB相比，精度性能稍差。

3.2 计算复杂度

中心化方法将所有计算集中于单一观测站或融合中心，而去中心化方法将计算分散到各观测站。观测站的数据传输量和计算量与观测站的度Dl有关，原始直接定位法和两步定位方法中主观测站的度D1=L，而本文所提两种方法各观测站度Dl=3。

原始直接定位法在主观测站或融合中心需要接收所有L-1个观测站的截获信号。对于傅里叶系数长度为2N的信号，构造互模糊矩阵所需的L个观测站的截获信号能量和L(L-1)/2个互模糊函数数值的计算量为O2N，互模糊矩阵特征值分解的复杂度为OL3。因此对于格点数目为G的空域，总计算量为O([GL2-(G-2)L]·N+GL3)，且所有计算量都集中在主观测站或融合中心。

本文第1种方法各观测站只需接收一个观测站的截获信号，另外将G维的互模糊函数值传输到融合中心。每个观测站只需计算自身截获信号能量和一个互模糊函数，每个观测站的总计算量为O2(G+1)N。L-1个观测站并加上特征值分解的总计算量为O2(L-1)(G+1)N+GL3。

第2种方法增加的总计算量是在第1种方法基础之上再利用式(24)互模糊函数之间关系公式计算余下(L-1)(L-2)/2个互模糊函数，而此时每计算一个互模糊函数的计算量为OG。因此与第1种方法相比增加计算量为O(0.5(L2-3L+2)G)，第2种方法总计算量为O(2(L-1)·(G+1)N+0.5(2L3+L2-3L+2)G)。

4 仿真实验

采用均方根误差(Root Mean Squares Error，RMSE)度量辐射源位置的定位估计精度性能，其定义为

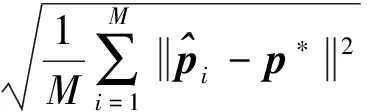
(40)

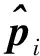
下面对各算法进行仿真实验分析。仿真中假定信号样式为线性调频信号，载频3 GHz，调频带宽10 MHz，脉冲宽度1 ms，脉冲间隔10 ms。各观测站的接收机噪声带宽都为20 MHz，信噪比相等。采用文献[31]的两步定位方法(Two-step)和文献[7]的原始直接定位方法(Original DPD)与本文所提两种方法进行仿真比较。本文所提两种方法依次分别为：第1种方法(Proposed method 1)采用去中心化配对方案计算L-1个互模糊函数构造的仅满秩互模糊矩阵的直接定位方法，第2种方法(Proposed method 2)利用任意互模糊函数间关系公式采用归约方式，去中心化的在各观测站并行计算余下互模糊函数以补全互模糊矩阵的直接定位方法。观测站与辐射源的位置与速度如表1所示。

在该观测站位置拓扑结构下，如果各观测站之间都可以单跳传输。采用去中心化配对方案，遍历各观测站配对集合。本文所提第1种方法中的目标函数式(14)的最优配对方案为{(1,4)，(4,7)，(7,9)，(9,5)，(5,3)，(3,2)，(2,6)，(6,8)}，总传输距离为27 713 m，因此对本文所提第1种定位方法进行仿真时采用该最优配对方案，对观测站标号集合{1,4,7,9,5,3,2,6,8}重新依次编号。本文所提第2种方法中的目标函数式(17)的最优配对方案为{(2,8)，(8,3)，(3,9)，(9,4)，(4,6),(6,5),(5,1),(1,7)}，初次循环时总传输距离为10 390 m，因此对本文所提第2种定位方法进行仿真时采用该最优配对方案，对观测站标号集合{2,8,3,9,4,6,5,1,7}重新依次编号。

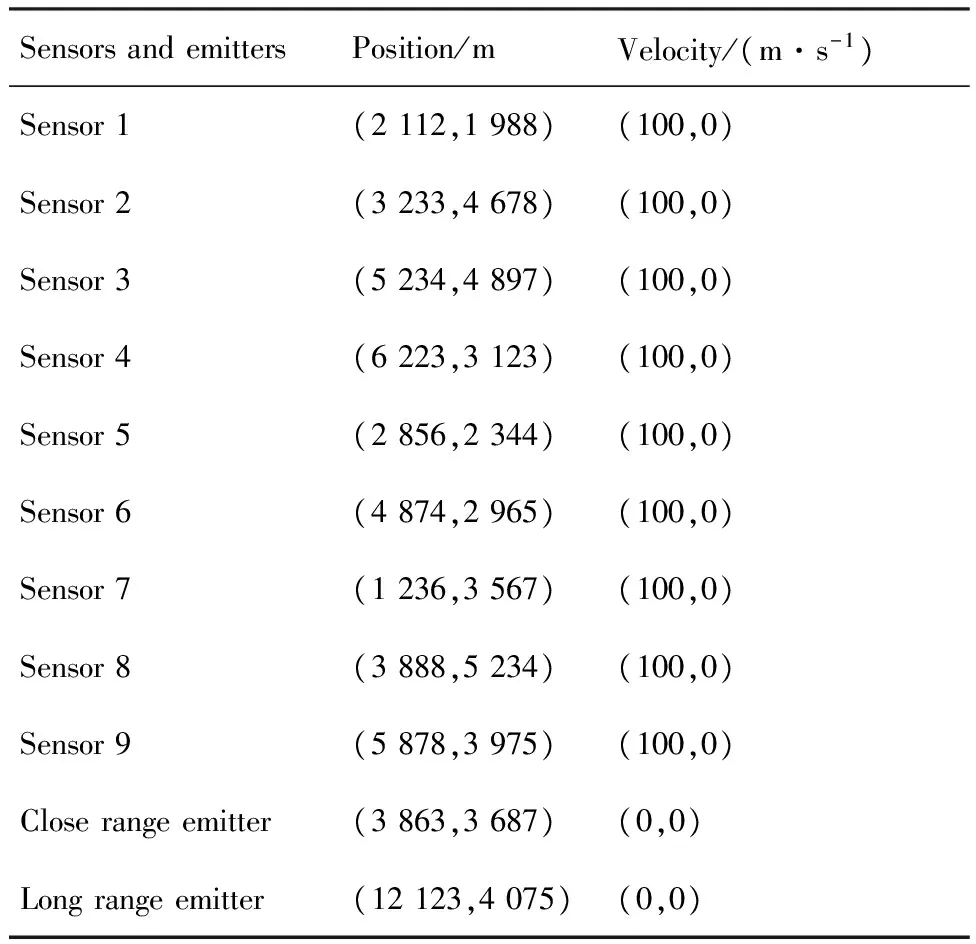
表1 观测站和辐射源的位置与速度Table 1 Position and velocity of sensors and emitters

两步定位方法采用的中心化观测站配对方案，对应的CRLBC根据式(34)的Fisher信息矩阵计算。本文所提第1种方法采用的去中心化观测站配对方案，对应的CRLBD根据式(36)的Fisher信息矩阵计算。本文所提第2种方法和原始直接定位方法采用的所有观测站两两配对方案，对应的CRLB根据式(32)的Fisher信息矩阵计算。对单个辐射源进行仿真，依次对近距离和远距离辐射源进行定位估计，各方法的RMSE和各观测站配对方案的CRLB随着信噪比的变化曲线如图1所示。

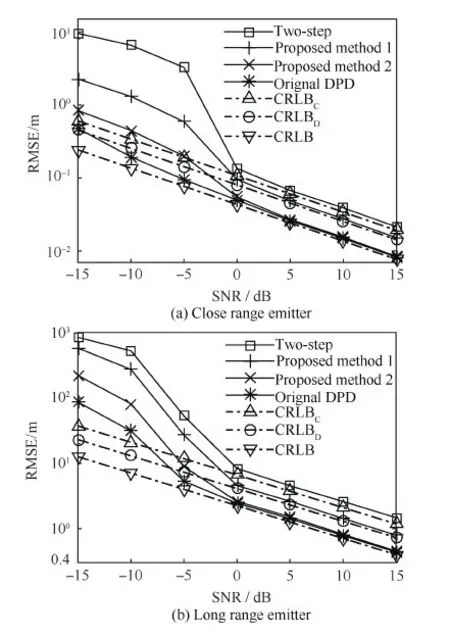
图1 各方法下不同辐射源定位随信噪比(SNR)变化的RMSE和CRLB曲线 Fig.1 Curves of RMSE of different methods and CRLB vs signal-to-noise ratio (SNR) for different emitters

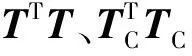
由图1还可以看出，在相同的信噪比情况下，采用去中心化配对方案的本文所提第1种方法由于均匀利用各观测站与辐射源在空间中相对位置，精度性能优于采用中心化配对方案的两步定位方法。本文所提第2种方法和原始直接定位方法由于采用所有观测站两两配对方案，利用了L个观测站所有LL-1/2组两两配对，精度明显优于只利用L个观测站中L-1组两两配对的两步定位方法和本文所提第1种方法；由于估计的去中心化时差频差存在误差，影响采用式(24)计算的余下互模糊函数的精度，使得最终的定位精度没有达到原始直接定位方法的精度，但计算量和数据传输量与原始直接定位方法相比得到了极大降低。

下面仿真不同观测站配对方案对单个辐射源的定位误差几何分布。由于辐射源目标在空间中的不同位置引起的定位误差是不同的，而定位误差几何分布描述了不同空间位置定位误差的分布情况。在仿真中，假定各观测站接收机的信噪比都为0 dB。各观测站配对方案的定位误差几何分布分别如图2所示。

由图2可以看出，由于各观测站位置都相同，因此定位误差在空间位置中的分布趋势相似。与前面RMSE仿真分析结论相同，去中心化观测站配对方案的定位精度高于中心化观测站配对方案的定位精度，所有观测站两两配对的方案在空间中的定位精度最高。

图2 定位误差几何分布 Fig.2 Geometric distribution of location errors

仿真实验采用大时宽带宽的线性调频脉冲信号，时频耦合效应会使得互模糊函数有较高的副峰。当信噪比较低时，时频耦合效应引起的较高副峰与噪声形成的峰相加会出现超过主峰的情况，使得真实峰值模糊，无法得到正确的定位估计结果。在本文的仿真参数下，本文所提方法在信噪比低于-30 dB时会出现定位结果错误的情况，而原始直接定位方法在信噪比低于-35 dB时才会出现定位结果错误的情况。可通过加窗抑制副峰，改善时频耦合效应对定位结果的影响。但加窗抑制副峰是以增大主峰宽度为代价的，会降低定位精度性能。

另外，同频多辐射源问题一直以来都是实现无源定位的难题，互模糊函数会出现伪峰，无法得到正确的定位估计结果，尤其是当同频多辐射源相距较近或信号功率相差较大时。对同频辐射源可利用信号其他域特征的差异将同频多目标的信号进行关联，具体信号特征包括到达方向、到达时间段、调制样式和极化等。

5 结 论

针对原始利用时差频差的直接定位方法存在数据传输量和计算量大的瓶颈，本文提出了两种去中心化直接定位方法，不同程度地简化了构造互模糊矩阵的方法，从而降低总的计算量，并将数据传输和计算量分散到各观测站之间，而不是集中于主观测站。

1) 第1种方法不需计算全部互模糊矩阵元素，L个观测站只计算L-1个互模糊函数，构造仅满足满秩条件的互模糊矩阵，采用去中心化配对方案，只将各观测站截获信号在站间进行一次传输，将数据传输和计算分散到各观测站间并行执行，提高了直接定位数据传输和计算的效率。

2) 第2种方法在利用信号计算L-1个去中心化互模糊函数之后，根据推导的任意互模糊函数间关系公式，采用归约方式去中心化的在各观测站并行计算余下的互模糊函数，补全互模糊矩阵所有元素，降低了直接定位数据传输和计算量。

3) 性能分析和仿真实验表明本文两种去中心化直接定位方法精度性能优于两步定位方法；在低信噪比时两种方法可得到比较理想的精度性能；在高信噪比时第2种方法与原始直接定位方法的精度性能相当。

[1] 赵国庆. 雷达对抗原理[M]. 第2版. 西安: 西安电子科技大学出版社, 2012: 9-11.

ZHAO G Q. Principle of radar countermeasure[M]. 2nd ed. Xi’an: Xidian University Press, 2012: 9-11 (in Chinese).

[2] POURHOMAYOUN M, FOWLER M L. Distributed computation for direct position determination emitter location[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(4): 2878-2889.

[3] WAX M, KAILATH T. Decentralized processing in sensor arrays[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1985, 33(4): 1123-1129.

[4] WEISS A J. Direct position determination of narrowband radio frequency transmitters[J]. IEEE Signal Processing Letters, 2004, 11(5): 513-516.

[5] WEISS A J. Direct position determination in the presence of model errors-known waveforms[J]. Elsevier Digital Signal Processing, 2006, 16(1): 52-83.

[6] AMAR A, WEISS A J. Localization of radio emitters based on Doopler frequency shifts[J]. IEEE Transactions on Signal Processing, 2008, 56(11): 5500-5508.

[7] WEISS A J. Direct geolocation of wideband emitters based on delay and Doopler[J]. IEEE Transactions on Signal Processing, 2011, 59(6): 2513-2521.

[8] OISPUU M, NICKEL U. Direct detection and position determination of multiple sources with intermittent emission[J]. Signal Processing, 2010, 90: 3056-3064.

[9] 张敏, 郭福成, 周一宇. 基于单个长基线干涉仪的运动单站直接定位[J]. 航空学报, 2013, 34(2): 378-386.

ZHANG M, GUO F C, ZHOU Y Y. A single moving observer direct position determination method using a long baseline interferometer[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(2): 378-386 (in Chinese).

[10] 张敏, 郭福成, 周一宇, 等. 运动单站干涉仪相位差直接定位方法[J]. 航空学报, 2013, 34(9): 2185-2193.

ZHANG M, GUO F C, ZHOU Y Y, et al. A single moving observer direct position determination method using interferometer phase difference[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(9): 2185-2193 (in Chinese).

[11] 王鼎, 张刚, 沈彩霞, 等. 一种针对恒模信号的运动单站直接定位算法[J]. 航空学报, 2016, 37(5): 1622-1633.

WANG D, ZHANG G, SHEN C X, et al. A direct position determination algorithm for constant modulus signals[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(5): 1622-1633 (in Chinese).

[12] BOSSE J, FERREOL A, GERMOND C, et al. Passive geolocalization of radio transmitters: Algorithm and performance in narrow band context[J]. Signal Processing, 2012, 92: 841-852.

[13] 黄志英, 吴江, 唐涛, 等. 非一致噪声下的多阵列直接定位算法[J]. 西安交通大学学报, 2015, 49(10): 136-142.

HUANG Z Y, WU J, TANG T, et al. A direct position determination algorithm based on multi arrays in the presence of unknown nonuniform noise[J]. Journal of Xi’an Jiaotong University, 2015, 49(10): 136-142 (in Chinese).

[14] VANKAYALAPATI N, KAY S M. Asymptotically optimal localization of an emitter of low probability of intercept signals using distributed sensors[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1): 737-748.

[15] VANKAYALAPATI N, KAY S M, DING Q. TDOA based direct positioning maximum likelihood estimator and the Cramer-Rao bound[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(3): 1616-1635.

[16] FOWLER M L, CHEN M, BINGHAMTON S. Fisher-information-based data compression for estimation using two sensors[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(3): 1131-1137.

[17] CHEN M, FOWLER M L. Data compression for multiple parameter estimation with application to emitter location systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(1): 308-322.

[18] 王云龙, 吴瑛. 联合时延与多普勒频率的直接定位改进算法[J]. 西安交通大学学报, 2015, 49(4): 123-129.

WANG Y L, WU Y. An improved direct position determination algorithm with combined time delay and Doppler[J]. Journal of Xi’an Jiaotong University, 2015, 49(4): 123-129 (in Chinese).

[19] XIA W, LIU W. Distributed adaptive direct position determination of emitters in sensor networks[J]. Signal Processing, 2016, 123: 100-111.

[20] XIA W, LIU W, ZHU L F. Distributed adaptive direct position determination based on diffusion framework[J]. Journal of Systems Engineering and Electronics, 2016, 27(1): 28-38.

[21] KNAPP C H, CARTER G C. The generalized correlation method for estimation of time delay[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1976, 24(4): 320-327.

[22] STEIN S. Algorithms for ambiguity function processing[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1981, 29(3): 588-599.

[23] 朱颖童, 董春曦, 刘松杨, 等. 存在观测站位置误差的转发式时差无源定位[J]. 航空学报, 2016, 37(2): 706-716.

ZHU Y T, DONG C X, LIU S Y, et al. Passive localization using retransmitted tdoa measurements in the presence of sensor position errors[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 706-716 (in Chinese).

[24] MENG W, XIE L H, XIAO W D. Decentralized TDOA sensor pairing in multihop wireless sensor networks[J]. IEEE Signal Processing Letters, 2013, 20(2): 181-184.

[25] CATTIVELLI F S, SAYED A H. Diffusion LMS strategies for distributed estimation[J]. IEEE Transactions on Signal Processing, 2010, 58(3): 1035-1048.

[26] TORRIERI D J. Statistical theory of passive location systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 1984, 20(2): 183-198.

[27] 张林波. 并行计算导论[M]. 北京: 清华大学出版社, 2006: 52-53.

ZHANG L B. Introduction to parallel computing[M]. Beijing: Tsinghua University Press, 2006: 52-53 (in Chinese).

[28] KAY S M. Fundamentals of statistical signal processing: Estimation theory[M]. Upper Saddle River, NJ: Prentice Hall, 1993: 39-40.

[29] 郭福成, 樊昀, 周一宇, 等. 空间电子侦察定位原理[M]. 北京: 国防工业出版社, 2012: 155-158.

GUO F C, FAN Y, ZHOU Y Y, et al. Localization principles in space electronic reconnaissance[M]. Beijing: National Defense Press, 2012: 155-158 (in Chinese).

[30] AMAR A, LEUS G, FRIEDLANDER B. Emitter localization given time delay and frequency shift measurements[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 1826-1837.

[31] HO K C, XU W W. An accurate algebraic solution for moving source location using TDOA and FDOA measurements[J]. IEEE Transactions on Signal Processing, 2004, 52(9): 2453-2463.

(责任编辑： 苏磊)

URL：www.cnki.net/kcms/detail/11.1929.V.20170109.1550.002.html

DecentralizeddirectpositiondeterminationmethodbasedonTDOAandFDOA

ZHUYingtong*,DONGChunxi,DONGYangyang,XUJin,ZHAOGuoqing

KeyLaboratoryofElectronicInformationCountermeasureandSimulationTechnology,MinistryofEducation,XidianUniversity,Xi’an710071,China

Toovercomethebottleneckofdatatransmissioncapacityandcomputationoftheoriginaldirectpositiondetermination(DPD)methodbasedonTDOAandFDOA,twodecentralizedDPDmethodsareproposed.Thefirstproposedmethodusesthedecentralizedsensorcouplingscheme,inwhichthesignalinterceptedbyeachsensoristransmittedonlyonceanddatatransmissionandcomputationoperationsaredispersedtoeachsensortocomputecrossambiguityfunction(CAF)inparallel,soastoconstructcrossambiguitymatrix(CAM)withmerelyfullrank.BasedonthederivationofaformulafortherelationbetweenarbitraryCAFs,thesecondmethodappliesareductionoperationtocomputetheremainingCAFsateachsensorinparallel,andcomplementsallelementsofCAM.TwodecentralizedDPDmethodsreducetheamountofdatatransmissionandimprovetheefficiencyofcomputation.Performanceanalysisandsimulationresultsshowthattheaccuracyoftheproposedmethodsaresuperiortothatofthetwo-stepmethods.AtlowSNR,bothofthetwoproposedmethodscanachievedesiredaccuracy,andathighSNR,thesecondproposedmethodcanobtaintheaccuracysimilartothatoftheoriginalDPDmethod.

directpositiondetermination;passivelocalization;crossambiguityfunction;decentralized;sensorcoupling;Cramer-Raolowerbound

2016-08-30；Revised2016-11-28；Accepted2016-12-22；Publishedonline2017-01-091550

s：NationalBasicResearchProgramofChina(61**81);NationalHigh-techResearchandDevelopmentProgramofChina(2014AA80**086H);theFundamentalResearchFundsfortheCentralUniversities(JB140203)

.E-mailzhuyt_xd@163.com

2016-08-30；退修日期2016-11-28；录用日期2016-12-22； < class="emphasis_bold">网络出版时间

时间：2017-01-091550

www.cnki.net/kcms/detail/11.1929.V.20170109.1550.002.html

国家“973”计划 (61**81)； 国家“863”计划 (2014AA80**086H)； 中央高校基本科研业务费专项资金 (JB140203)

.E-mailzhuyt_xd@163.com

朱颖童， 董春曦， 董阳阳， 等． 去中心化时差频差直接定位方法J．航空学报,2017,38(5):320727.ZHUYT,DONGCX,DONGYY,etal.DecentralizeddirectpositiondeterminationmethodbasedonTDOAandFDOAJ.ActaAeronauticaetAstronauticaSinica,2017,38(5):320727.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.320727

V247.5； TN971

A

1000-6893(2017)05-320727-13