材料驱动，助推学生空间观念的发展

胡梦迪

［摘 要］发展学生的空间观念是小学数学教学的重要目标之一，其有益于提升学生的数学核心素养。以一类长方体体积的练习题开始思考，从提供平面素材、增加操作环节、重视经验积累、延伸知识结构四个角度出发改造习题，有效发展学生空间观念。

［关键词］空间观念；长方体体积；练习题

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2023）11-0052-04

什么是空间观念？孔凡哲教授认为空间观念是学生主动、自觉或自动化地“模糊”二维和三维空间之间界限的一种本领，是一种可以把握的能力；《义务教育数学课程标准（2022年版）》提出空间观念是“核心素养”的主要表现之一，是几何课程改革的一个核心概念。在小学数学课程中，空间观念主要涉及图形与几何领域，下面，笔者就对该领域内“长方体的体积”（人教版教材五年级下册）这一课的习题进行重新设计，以实现培养学生空间观念的教学目标。

一、教材习题

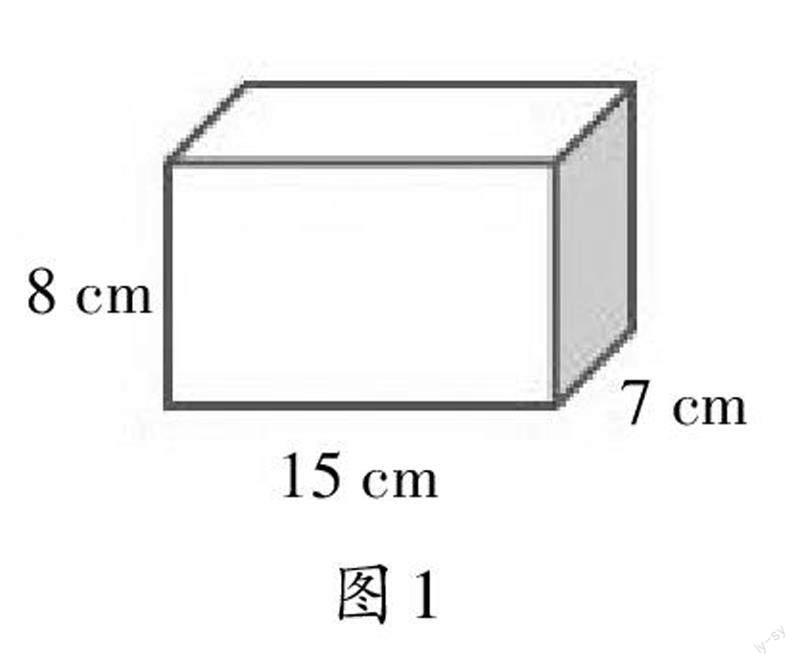
习题1（教材第31页）：一块长方体肥皂的尺寸如图1所示，它的体积是多少？

习题2（教材第33页）：建筑工地要挖一个长50 m、宽30 m、深50 cm的长方体土坑，一共要挖出多少方的土？

学生反馈（见表1）。

习题1和习题2是一类在简单情境下考查长方体体积计算公式的练习题。这两题都是提供线段长度，让学生求体积。根据题目信息，学生很快就能想到套用公式V=abh来解答问题。从学生较高的解题正确率来看，学生对公式掌握得很扎实，偶有出错也是计算过失，或是没有进行单位换算，只要仔细审题，这些错误是完全可以避免的。因此，用这类练习题来帮助学生巩固对公式的记忆和应用是非常合适的。然而对立体图形的教学，不能仅仅止步于学生对公式的熟练应用，更应该发展学生的空间观念，让学生看到线段长度后头脑中就能构造出长方体的形状，再进行相关计算。

二、策略探索

五年级学生的抽象思维和空间想象能力正在逐步发展，习题训练的重点应是立体图形在头脑中表征过程的经验积累。重新设计习题，即在提供平面素材的基础上增加动手操作和想象环节，让学生经历用若干个平面构造成立体图形的抽象思考过程，以“模糊”二维和三维空间之间的界限，对长方体与其他立体图形的“面”“体”关系的探究进行拓展延伸，实现发展学生空间观念的教学目标。

1.提供平面素材，培养信息分析能力

如何让学生重新组织材料，经历构建长方体的过程？笔者设计了一道开放性习题。

学习要求：（1）独立思考。通过剪、拼、画、想，你得到的长方体是什么样的？体积是多少？（2）讨论交流。（3）成果分享（以表格的形式呈现，见表2）。

这道习题提供的素材都是长方体的侧面，学生需要先分析素材的信息，再建构立体图形。学生通过读题，会发现习题提供的四个长方体侧面数量是不同的，其中1号长方体给足了6个面，而其余3个长方体只呈现了6个面中的若干个面。此外，根据侧面的长、宽这类长度信息，學生要找出不同面上相同长度的边，分析哪两个面上的哪两条边进行拼接。经历了这个信息分析的过程，学生就能根据平面来建构立体图形了。

2.增加操作环节，培养推理想象能力

师：你得到的长方体是什么样的？

生1：我们小组用剪拼的方法。因为长方体相对的2个面一样，我们就把这6个面分成3组，将相同长度的边拼接就得到1号长方体。

生2：我们把3号长方体画出来了。我们先画一个长方体，再把长度标上，就得到了长方体的长、宽、高，从而确定了它的形状。

师：你们不用剪下来拼接就能得出长方体，真厉害！

生3：我看一眼就知道1号和2号长方体的长、宽、高了。因为长方体的面上共有三种不同的长度，而这三种长度正好就是长、宽、高。

生4：我找不到4号长方体的高。

师：其他人找到了吗？4号长方体的高到底是多少呢？这个疑问先留着，我们待会再解决。

从反馈中可以看出，学生的思维非常清晰。根据题目提供的侧面，通过剪、拼、画等操作，搭建了长方体。有学生甚至能根据侧面上的线段的长度关系和位置关系直接想象出长方体的形状。在这个过程中，学生的推理想象能力发展过程如图3所示。

3.重视经验积累，培养归纳概括能力

经历了上一个环节的操作与想象，学生已积累了对立体图形的推理和想象经验，接下来依托这些经验，学生将能探究更深层次的空间位置关系，归纳概括新的学习经验。

（1）探究面的位置关系

确定长方体的形状，是否一定要知道一个长方体的所有侧面呢？如减少侧面的数量，还能确定其形状吗？至少需要哪些面？由此，笔者引导学生对比探究图2中的四个长方体。

师：同学们，我们已经知道了长方体的侧面中隐藏着长方体的长、宽、高。3号长方体只给了2个面，你们也能找到长方体的长、宽、高，4号长方体跟3号长方体一样，也给了2个面，为什么找不到长方体的高呢？

生1：因为给出的4号长方体的2个面是一样的，是相对的面，所以不能确定高。

生2：我觉得不一定，如果这2个面是相邻的，体积就有两种情况，即15×15×8和15×8×8。

师：看来2个面的位置关系是关键，必须是相邻的面，不能是相对的面。那只留1个面行吗？

生3：不行！只留1个面就只能获得长、宽、高三者中的两个信息。

师：研究到这里，谁能总结一下？

生4：只要确定了相邻的2个面，长方体的形状就确定了。

从学生的回答中可以发现，他们不再依赖于画图，通过想象也能理解平面图形和立体图形之间的联系（如图4）。在这一阶段，学生在头脑中对长方体的表象越来越清晰，他们能够想象2个面的不同空间位置关系——相邻和相对，再从中辨别出只有相邻的面才能确定长方体的形状。

值得一提的是，开始大部分学生都认为4号长方体不能构成，但经过讨论和交流，得出了三种不同的情况：15×8×8，15×15×8，15×b×8（b不一定）。这是一个开放性的设计，促成了学生更为热烈的讨论，他们在对面的位置关系的假设和讨论中，空间观念得到了发展。

（2）探究立体图形的平面化

在问题都已解决后，笔者借机引导学生进行深层次的、更抽象的三维到二维的探讨。

师：同学们，学到这里，对于长方体的形状、大小，你有什么想说的吗？

生5：根据公式V=abh，我知道了长方体的长、宽、高决定了它的形状和大小。

生6：做了这道题，我知道了只有相邻2个面也能确定一个长方体的形状和大小。

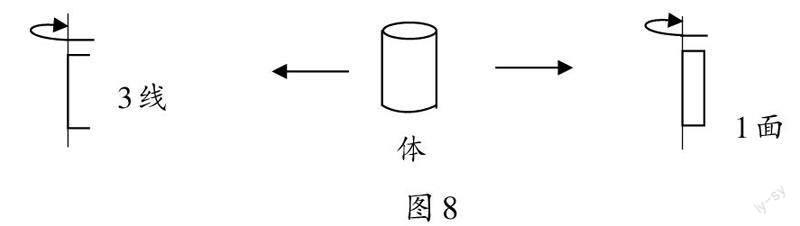
师：从线的角度看，一个长方体有12条棱（线），精简到3条线（长、宽、高）也能确定一个长方体；从面的角度看，一个长方体有6个面，精简到相邻2个面也能确定一个长方体。我们刚才所讲的“线”“面”“体”就分别代表了几何空间里的“一维空间”“二维空间”“三维空间”。

师：一个长方体可以精简到“3线”“2面”，你能画一画这样的变化过程吗？

（学生思考、讨论、画图，得出图5）

这道习题的目的是驱动学生自主地实现面和体之间的转换。学生解决完这道习题后，他们的空间想象和推理能力已经经历了一次跳跃，此时笔者趁热打铁，通过语言引导和思维导图的梳理，助推他们对长方体特征进行跨维度的、深层次的把握：原本是三维的长方体，画在纸上就变成了二维，再通过“线”“面”“体”三维之间的转化沟通，将长方体精简成“3线”“2面”。这说明学生已经抓住了画长方体平面图形的精髓，学生的空间观念正逐步发展完善。

4.延伸知识结构，培养空间思维能力

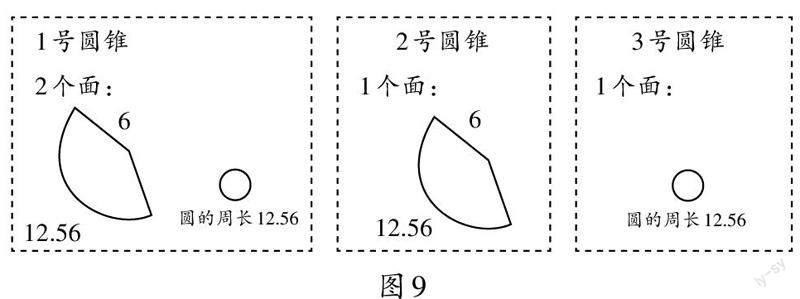
考虑到在学习长方体之后，学生还要学习正方体、圆柱、圆锥这三类立体图形，笔者又设计了系列题组。

（1）正方体

（2）圆柱

（3）圆锥

综上所述，通过这几道习题，学生经历了“线”“面”“体”三个空间维度之间的转换过程，加深了对这类立体图形的特征理解，教学也初步实现了要有意识地培养学生跨维度的空间观念的目标。在图形与几何领域的教学中，教师要让学生亲身经历活动，经验积累多了，不同维度空间之间的界限就会越来越模糊，空间观念就可以不断生长和发展。

［ 参 考 文 献 ］

[1] 唐彩斌.能力為重的问题解决式复习：以“长方体的表面积、体积复习课”教学为例 [J].教学月刊小学版（数学），2013（12）：35-38.

[2] 孔凡哲.小学生空间观念的发展对策[J].新教师，2019（10）：38-40.

（责编 覃小慧）