单元整体视角下“口算除法”教学的“破”与“立”

吴梦媛

［摘 要］单元整体视角下的课时设计，要关注课堂的深度和延展度。口算是计算教学的基础，能为笔算教学做铺垫。文章以人教版四年级上册的“口算除法”一课为例，直面教学中的尴尬，寻根溯源打破僵局，以单元整体视角，探索口算教学的模式。

［关键词］单元整体视角；口算除法；多元表征；估算

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2023）11-0028-04

口算是小学数学“数与代数”领域非常重要的内容，学好口算、掌握口算的技巧，有助于后续笔算和解决问题的学习。这要求教师从单元整体视角思考口算教学，让口算教学发挥单元引领作用，把看似单薄的口算教学内容变得厚实，重视在口算教学中加深学生对算理和算法的理解，重视估算方法和策略的渗透，从而夯实学生的计算基础。

一、师生两难，直面教学尴尬

1.教师的尴尬：课堂热闹，课后凄凉

教师往往觉得传统口算教学的内容单薄，没有深入研讨的价值。上课时，口算教学的课堂气氛热烈，学生的回答整齐划一，偶尔有几个答错的声音，也很快被淹没在响亮的正确回答声中。然而，批改作业时，教师时常会无奈地感叹：“这么简单，怎么还有这么多人答错！”对此，教师往往让学生反复练习，以提高口算水平，但效果不佳，这让教师陷入尴尬的境地。

笔者发现，一些教师容易忽略学生已有的口算经验，把学生当作没有口算基础的群体开展教学活动；教学多道口算例题时容易平均用力，教学重点不突出；容易忽略口算的单元起始课地位，和后续教学内容脱节；容易过多关注精算，忽略估算，甚至有教师认为除法估算的策略描述起来较难，便在课堂上避开不讲。

2.学生的尴尬：做错不全因为马虎

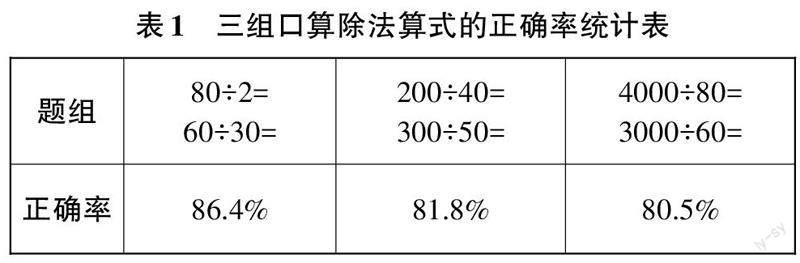
学生觉得口算难度不大，自己已经完全掌握，面对算错的口算题，他们马上就能订正。对于这些错误，学生认为只是粗心导致的。然而，把作业中学生已经会的算式里的数一换，学生的正确率就下降。比如四年级上册“除数是整十数的口算除法”的练习，随着被除数、除数末尾0的个数的增加，学生计算的正确率有所下降（见表1）。

二、寻根溯源，打破传统教学僵局

寻根溯源可以让口算教学的课堂灵动且富有生命力。口算教学的“根”在哪里？学生认知的“源”又在哪里？教师可基于教材寻口算教学的“根”，寻知识的生长点和网状关联点；基于学生的认知结构寻口算教学的“源”，寻学生的认知起点，以及知识迁移的难点。

1.破教学定位：单元整体视角下刨根究底，寻知识关联

加减法口算能力的培养有助于学生后续乘除法口算能力的提升。人教版教材中，加减法的口算教学编排较为集中，主要分布在一年级，以“20以内的加减法”“100以内的加减法”这两个单元为主。

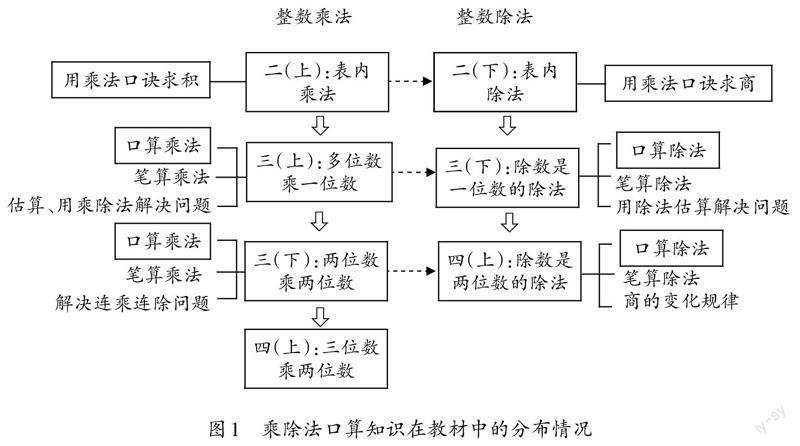
乘除法口算的教学编排较为分散（如图1），穿插在二年级到四年级乘除法教学的各个单元中，往往是各个单元的起始课，为该单元后续学习笔算和解决问题奠定基础。小学整数除法的教学共分为三个阶段。“除数是整十数的口算除法”是学生第三次接触口算整数除法的内容，学生已有的口算除法经验有助于这节课的新知建构。此外，“除数是整十数的口算除法”是“除数是两位数的除法”这个单元的起始课。这个单元分为口算除法和笔算除法。笔算除法与口算除法有密切联系，笔算除法要借助口算除法的相关知識进行试商和调商。学生深入理解口算除法，就可以更好地理解笔算除法的算理，为后续学习笔算除法、商的变化规律做铺垫。

2.破教学方式：前测精准分析下穷源溯流，谈认知盲点

基于以上思考，笔者以“除数是整十数的口算除法”为例，开展了前测研究。

研究1：学生课前能准确用口算得出除法算式的答案吗？

笔者用8道整十数除整十、几百几十数的算式对学生进行了前测，8道算式均答对的人数占比在82%～86%之间。可见，正确算出简单的口算除法的结果对学生而言较为简单。

研究2：学生课前能表示口算除法的算理吗？

笔者尝试让学生表示60÷20的算理，有75%的学生只想到了一种表示方式，只有11%的学生想到了多种表示方式，剩下的学生表示方法错误。这说明大部分学生能够理解算式的意思，但是表示方式较为单一。从错例（如图2）中可以发现，学生还有很多认知盲区。错例1是将算式60÷20与算式60÷2的意义弄混淆；错例2和错例3没有正确建立60÷20与6÷2的联系。这说明学生有将新知转化为旧知的意识，但不知道转化的原理，究其原因是学生对口算除法的算理理解得不透彻。

研究3：学生课前掌握了除法估算的方法吗？

笔者用8道估算算式进行前测，学生的正确率在48%～82%之间。笔者以访谈的方式了解学生估算时的想法，发现学生对除法估算的方法和策略了解得不够深入，而且很少有学生能表述清楚自己的想法。通过前测笔者发现，不同学生的估算能力有较大差异。因此，教师在课堂上要加大估算教学的力度，关注对估算方法和策略的提炼。

三、单元视角，立口算教学模式

口算教学模式要关注算理和算法的建构，也要关注口算教学在这一单元中的地位和作用。“除数是整十数的口算除法”在教材中的内容较为单薄，但对于“除数是两位数的除法”这整个单元却至关重要：“口算除法”作为计算课，需要通过这一课让学生理解除数是整十数的除法算式的计算方法和原理，并能又快又准确地给出答案；“口算除法”作为单元种子课，要为后续学生学习笔算除法服务。而估算是为笔算除法中试商做的铺垫，因此估算的价值要在这节课中有所体现。

1. 立算理：借助多元表征，巧抽象

通过前测，笔者了解到学生有自主表征算式含义的能力，但表征方式较为单一；学生具备一定的读图分析能力，但是缺少将图和图进行相互比较的能力。课堂上，教师可以引导学生自主表征算式80÷20，然后收集学生的典型回答（如图3）。

①是把80个圆每20个一份做上标记。②是不看80和20末尾的0，而将算式转化为表内除法8÷2来解决。③是把除法算式转化成乘法算式。④是把80看成8个十，20看成2个十，思考8个十里有几个2个十。

接着，教师引导学生对不同的表征方式进行解读。学生发现四种方式都能解决“80里有（ ）个20”的问题。教师还需要沟通联系不同的表征方式，让学生明白可以把①里的80个一和20个一转化为④里的8个十和2个十；计数单位的改变可以把80÷20转化为②中遮住0后的8÷2。通过思考各表征方式之间的关联，逐步抽象出被除数和除数都是整十数的除法的算理，渗透转化的数学思想，把新知转化为除数是一位数的除法或表内除法。

2. 立算法：借助结构化教具，巧联系

在“口算除法”的学习中，学生仅仅会算80÷20=4是不够的，还要把口算除法的算理和算法进行迁移，借助转化思想，计算更多的口算除法算式。教师可以借助结构化的教具，帮助学生找到不同算式之间的联系。

【教学片段1】

师：80÷20=4可以转化成8÷2=4，800÷200可以吗？你是怎么想的？

生1：把800看成8个百，把200看成2个百，想8÷2=4。

师：还有什么算式也可以转化成8÷2=4？

生2：8000÷2000=4，80000÷20000=4。

师：到底是不是这样，我们用计数器来验证一下。（验证过程如图4所示）

师（小结）：这些算式都可以通过改变计数单位，转化为8÷2=4，用口诀“二四得八”来解决。

笔者借助多元表征，先让学生在解读表征和沟通表征的过程中掌握80÷20=4的算理和算法，感悟转化的数学思想方法；再从8÷2=4出发，让学生展开联想；最后引出一系列算式，让学生发现算式之间的联系，做到触类旁通。

3. 立口算能力：借助认知迁移，巧转化

人教版教材四年级上册第71页，例1为被除数是整十数的口算除法，例2为被除数是几百几十数的口算除法。将两道例题的算理和算法打通，能让学生更好地掌握口算除法，提高学生的口算能力。学习完例1的口算除法知识后，大部分学生都有能力自主挑战例2的口算除法，此时教师可以把课堂的主动权交给学生，让学习能力强的学生帮助学习有困难的学生完成新知的学习。

【教学片段2】

学生独立完成6道口算练习，教师展示错例（如图5），组织学生讨论订正。

生1：150÷50应该等于3。把150看成15个十，把50看成5个十，想15÷5=3。

生2：180÷30应该等于6。把180看成18个十，把30看成3个十，想18÷3=6。

生3：200÷40应该等于5。把200看成20个十，把40看成4个十。想20÷4=5。

师（小结）：看来几百几十除以整十数和整十数除以整十数的计算方法是相同的，都是想几个十除以几个十，借助相同的计数单位，把算式转化成表内除法，利用乘法口诀来计算。

学生理解整十数除以整十数的算理和算法以后，几百几十数除以整十数对学生而言难度不大。因此，教师在这个环节中要着重培养学生的口算能力，同时，计算的正确率和计算的速度也非常重要。学生在口算时借助转化思想，有助于计算速度的提高。题组式练习有助于学生夯实计算基础，且有助于学生比较被除数是整十数、被除数是几百几十数两类算式，以“类”的视角分析数学算式，发现两类算式计算的相同点。从学生的错误出发，基于反馈的教学方式，可以避免相似例题的重复教学，让课堂更加轻松高效。

4. 立估算：借助递进设计，巧理解

“除数是两位数的除法”这个单元中，口算除法之后的教学内容是笔算除法。然而，学生笔算除法的计算正确率并不高，因为试商对学生而言比较困难。估算是“口算除法”教学内容的一部分，掌握估算方法，有助于学生后续掌握笔算除法，提高计算的正确率。在计算教学中，重视估算的价值，有助于培养学生的数感。

除法的估算方法与加法、乘法、减法的估算方法有较大不同，学生难以迁移以往的经验。对此，笔者教学时让学生先自主尝试，再有层次地进行反馈，从而帮助学生形成估算除法的一般策略。

【教学片段3】

（学生尝试估算4道算式，教师展示学生的结果，如图6所示）

（教学除数是整十數的估算）

师：对于图6中的前面两道算式，谁能说一说自己是怎么算的？

生1：把被除数263估成270，270÷90=3；把88估成80，80÷20=4。

师：谁有疑问？

生2：被除数88为什么估成80，而不是按照“四舍五入”的方法估成90呢？

生1：因为估成90还是没法简算，估成80比较好算。

生3：因为88比较接近20的4倍，所以估成80。

师：你们的意思是当除数是整十数时，就把被除数估成整十数的倍数。

（教学除数不是整十数的估算）

师：遇到除数不是整十数时，比如155÷51，是怎么估的？

生4：先把除数51估成50，再把被除数155估成150，150÷50=3。

师（小结）：嗯，先估除数再估被除数会更方便。我们一起来说一说，先把51估成50，再把155估成150，因为150÷50等于3，所以155÷51≈3。

师：189÷□，猜一猜这个同学为什么想到在□里填一个整十数？

生5：填整十数估算起来比较简便。

师：有没有人填的不是整十数？说一说你是怎么估的。

（教师根据学生回答记录估算过程，如图7所示）

师：都是189除以一个数，为什么189有的时候估成180，有的时候估成200、210、160呢？

生6：除数不同，被除数是根据除数估成的数来估的。

师：今天学习的除法的估算和之前学习的加法、减法、乘法的估算不一样，被除数要根据除数估成的整十数来估，估成整十数的倍数。今天学习的估算主要是为了以后学习两位数笔算试商做准备。

除法的估算是本节课的难点，学生对估算的方法和原理理解得不够清晰。在估算教学中，把难点进行分解，能帮助学生更好地理解和掌握估算的方法和原理。口算除法的估算教学分为除数是整十数的除法、除数不是整十数的除法两个部分。除数是整十数的除法的教学着重让学生感悟除法的估算与以往学习的估算是不同的，想估被除数要先分析除数是几，把被除数估成除数的倍数。学生初步理解除法的估算原理后，再尝试分析除数不是整十数的除法估算。开放题“189÷□”让学生不仅巩固了除法估算的方法，更在辨析中深刻明白了除法估算的策略和原理。

以单元整体视角思考口算除法的教学策略，让口算除法的教学脚踏实地。学生依靠原有认知，基于多元表征，掌握口算的方法，理解口算原理，进而沟通联系算理和算法。对于口算教学，教师要有类的意识，巧用结构化教具建立口算的模型，让学生从一道题走向一类题；要立足单元整体视角，以单元视角思考课时地位，充分发挥口算教学单元起始课的作用，为后续笔算教学奠定基础。

基于单元整体视角设计小学数学课堂，让课时与课时之间的联系更加紧密，让学生对单元知识形成更加全面的认识。

［ 参 考 文 献 ］

[1] 童艳芬.怎样理解除数是整十数口算除法的算理[J].教学月刊小学版（数学），2022（4）：26-27.

[2] 夏青，张云萍.数形结合明算理 迁移类推通算法：“口算除法”教学实录与评析[J].小学数学教育，2020（17）：69-71.

（责编 吴美玲）