左R-模上Riesz空间的同态和同构性质研究

孙锐娟，汤建钢，2*

（1.伊犁师范大学数学与统计学院，新疆伊宁 835000；2.伊犁师范大学应用数学研究所，新疆伊宁 835000）

0 引言

在20 世纪二三十年代，F.Riesz 等人分别将格序结构引入到向量空间，提出了Riesz空间概念，研究了Riesz空间的一些基础性质.由于它是把具体的分析问题抽象在一种更加纯粹的代数结构和格序结构中进行研究，由此发展出的概念和方法，应用也就更为广泛、更加深刻.由于环的不一定可换，所以有了左模与右模之分.模的概念是19世纪提出的，但到20世纪40年代才引起重视；到70年代，人们认识到模是当代最重要的代数结构之一，其重要性超过了线性空间，并且模是域上线性空间概念的推广.因此，将格序结构引入模的概念中，将Riesz空间推广到模很有必要.文献［1］和［2］由浅入深地叙述了范畴与同调代数的基本知识,开头按照模的体系介绍了它的定义、子模、商模、模同态与同构及其性质，中间部分讲述了范畴和几类特殊模，在文献的最后详细地介绍了函子和同调的相关内容.文献［3］中的前半部分详尽地介绍了格论的基本性质与结构，后半部分就迈进了格论的专业研究，例如补格与布尔代数及同余关系与同余格继而进入了伪补代数与stone代数这个颇为高深的领域.文献［4］提出Riesz空间是有代数结构的序结构.文献［5-9］将格序结构引入群、环中，得到了格序群、格序环，以及它们的一些基本性质.

同态与同构在代数中有着非常重要的作用，也是研究Riesz模范畴的先决基础.因此，研究左R-模上Riesz空间的同态与同构的相关性质很有必要.文献［10］研究了l-群的同构关系，将群论中的同构定理推广到格序群，同时也研究了格序群的主凸l-子群的结构.文献［11］用泛代数的方法研究了格序群上的同余关系，证明了一个格序群的同余格与它的l-理想格是同构的.文献［12］将基本同态定理推广到格序环和格序模中.本文在l-群、l-环的基础上，基于对具有代数结构序对象的Riesz空间及其性质的研究，类比格序群和格序环的同态与同构的性质，研究了左R-模上Riesz空间的同态与同构的相关性质.

1 预备知识

定义1.1设(G,+)是一个Abelian群，≤是群G上的一个偏序关系，满足∀a,b,c∈G,a≤b⇒a+c≤b+c，则称(G,+,≤)为一个Abelian偏序群.

定义1.2设(G,+,≤)是一个Abelian偏序群，如果偏序集(G,≤)是一个格，则称(G,+,≤)为一个Abelian格序群，简称为Abelian l-群.

定义1.3设(R,+,·)是一个具单位元的环，≤是环R上的一个偏序关系，满足∀r,s,t∈R，

（1）r≤s⇒t+r≤t+s，

（2）0 ≤r,0 ≤s⇒0 ≤rs，则称(R,+,·,≤)是一个偏序环.

注：记R+={r∈R|r≥0}，则定义1.3中的条件（2）等价于R+R+⊆R+.

定义1.4设(R,+,·,≤)是一个偏序环，如果偏序集(R,≤)是一个格，则称(R,+,·,≤)是一个格序环，简称为l-环.

定义1.5设M为左R-模，(R,+,·,≤)是具单位元的偏序环，(M,+,≤)是Abelian偏序群，满足∀m,n,p∈M,∀r∈R(r≥0)，都有m≤n，则m+p≤n+p,rm≤rn，则称(M,+,≤)为左R-模上的偏序模，简称为po-模.

注：记M+={m∈M|m≥0}，则定义1.5中的条件对∀m,n∈M,∀r∈R(r≥0)，若m≤n，则rm≤rn等价于条件∀m∈M,∀r∈R，若m≥0,r≥0，则rm≥0，并且等价于R+M+⊆M+.

定义1.6设(M,+,≤)为左R-模上的偏序模，如果(R,+,·,≤)是具单位元的l-环，(M,+,≤)是Abelian l-群，则称(M,+,≤)是左R-模上Riesz空间，也称为格序左R-模，简称为l-R-模.

定义1.7设(M,+,≤)是一个l-R-模，(N,+)是(M,+)的子模，如果(N,≤)是(M,≤)的一个子格，并且R+N+⊆N+,则称(N,+,≤)是(M,+,≤)的一个子l-R-模.

定义1.8若N是l-R-模M的子l-R-模，且N是凸集，即对任意的m∈M,n1,n2∈N′，当n1≤m≤n2时，有m∈N′，则N′称为M的凸子l-R-模.

定义1.9设(M,+,≤)是l-R-模，对任意m∈M，若m≥0，称m是一个正元素，m≤0，称m是一个负元素.自然地定义m的正部分是m+=m∨0，m的负部分是m-=(-m) ∨0，M的绝对值是 |m|=m++m-.

定义1.10设(M,+,≤)是一 个l-R-模，N是(M,+,≤)的子模，如果N满足正规性条件，即∀m∈M,∀n∈N,若|m|≤ |n|时，则m∈N,称(N,+,≤)是(M,+,≤)的一个（序）理想.

2 基本内容

定义2.1设(M,+,≤)，(N,+,≤)是l-R-模，f:M→N是左R模同态，若对任意的x,y∈M，有

（1）f(x∨y)=f(x)∨f(y)，

（2）f(x∧y)=f(x)∧f(y)，则称f为M到N的一个l-R-模同态，记作M～N.

设f:M→N是M到N的一个l-R-模同态，若f是单射，则称f是l-R-模单同态.若f是满射，则称f是l-R-模满同态.若f是双射，则称f是l-R-模同构（简称同构），也称l-R-模M与N同构，记作M≅N.若M=N，相应的同态（同构）叫做l-R-模M的自同态（自同构）.

设f:M→N是M到N的一个l-R-模同态，易见f(M)是N的凸子l-R-模.如果f:M→N是l-R-模单同态，则M的凸子l-R-模f(M)与M同构，我们称这样的f是l-R-模M到l-R-模N的嵌入映射.

定义2.2设f:M→N是l-R-模同态，把M的所有元素都映射到N的零元素的同态f(x)=0∈N，∀x∈M称为l-R-模零同态，记作0:M→N.

命题2.1设f:M→N是l-R-模同态，其中(M,+,≤),(N,+,≤)是左R-模上Riesz 空间,定义f:M→N的核与象分别为Kerf=f-1(0)={x∈M}，则Kerf是M的凸子l-R-模，Imf是N的凸子l-R-模.

证明：易知Kerf是l-R-模M的一个子模，由于Kerf=f-1(0)={x∈M}，对任意的x,y∈Kerf，有f(x∧y)=f(x)∧f(y)=0,故x∧y∈Kerf.同理可得x∨y∈Kerf.则(Kerf,≤)是(M,≤)的子格.∀x,y,p∈Kerf,∀r∈R(r≥0),当x≤y时，有rx≤ry,x+p≤y+p,因 此Kerf是M的 子l-R-模.若∀x,y∈Kerf,z∈M,x≤z≤y,则f(x)≤f(z)≤f(y).由f(x)=f(y)=0，可得f(z)=0,即z∈Kerf.故Kerf是M的凸子l-R-模.同理可知Imf是N的凸子l-R-模.

命题2.2设(M,+,≤)，(N,+,≤)是l-R-模，若M′ 是M的一个凸子l-R-模，定义M/M′={M′+x|x∈M}，则M/M′是一个l-R-模.

证明：在M/M′={M′+x|x∈M} 中,定 义M′+x≥M′+y的充要条件为存在s∈M′,使得s+x≥y,(M′+x)∨(M′+y)=M′+(x∨y),(M′+x)∧(M′+y)=M′+(x∧y),则M/M′是一个格,易知M/M′对于加法(M′+x)+(M′+y)=M′+(x+y)可构成一个Abel加群,故M/M′是一个l-加群.

由模论知,对任意r∈R,M′+x∈M/M′,定义r(M′+x)=M′+rx,则M/M′是一个R-模.对任意的r∈R,(M′+x)∈(M/M′)+,则存在s∈M′,使得s+x≥0,因 为r(s+x)=rs+rx≥0，且rs∈M′，则r(M′+x)=M′+rx≥M′.任意的x1,x2,x3∈M，若M′+x1≥M′+x2，则 有(M′+x1)+(M′+x3)=M′+(x1+x3)≥M′+(x2+x3)=(M′+x2)+(M′+x3),因此M/M′是l-R-模.

命题2.3设f:M→N是l-R-模满同态，其中(M,+,≤)，(N,+,≤)是左R-模上Riesz空间，定义l-R-模同态f的余核和余象分别为：Cokerf=Coimf=M/Kerf，则Cokerf和Coimf是l-R-模.其中是包含Imf的N的最小l-R-模.

命题2.4设f:M→N和g:N→P都是l-R-模同态，那么gf是M到P的l-R-模同态，称为f与g的复合.

证明：由文献［3］可知，gf是模同态.下证gf为格同态.对任意的x，y∈M，有g(f(x∨y))=g(f(x)∨f(y))=g(f(x))∨g(f(y))=gf(x) ∨gf(y)，同理可得g(f(x∧y))=gf(x) ∧gf(y)，故gf是l-R-模同态.

命题2.5设M,N,P都是l-R-模，f∈Hom(M,N),g∈Hom(N,P)，则

（1）若f,g都是l-R-模单同态，则gf是l-R-模单同态；

（2）若f,g都是l-R-模满同态，则gf是l-R-模满同态；

（3）若gf是l-R-模单同态，则f是l-R-模单同态；

（4）若gf是l-R-模满同态，则f是l-R-模满同态.

证明：由文献［3］和l-R-模单同态和l-R-模满同态定义可知结论显然成立.

命题2.6设f是M到N的l-R-模同态：

（1）f为l-R-模单同态当且仅当Kerf=0；

（2）f为l-R-模满同态当且仅当Cokf=0；

（3）f为l-R-模同构当且仅当Kerf=0，Cokf=0.

证明：（1）设f为l-R-模单同态，对任意的m∈Kerf，则f(m)=0=f(0)，由于f是单同态.故可得m=0，即Kerf=0.反之若Kerf=0，则对任意的m1,m2∈M，有f(m1)=f(m2)=0，可得f(m1-m2)=0.故有m1-m2=0，即m1=m2，故f为l-R-模单同态.

由（1）（2）可得（3）.

命题2.7设M，N，P都是l-R-模，f是M到N的l-R-模同态，则

（1）f为l-R-模单同态当且仅当对任意的l-R-模保序映射，g1,g2∈Hom(P,M)，若fg1=fg2，必有g1=g2.

（2）f为l-R-模满同态当且仅当对任意的l-R-模保序映射,ℎ1,ℎ2∈Hom(N,Q)，若ℎ1f=ℎ2f，必有ℎ1=ℎ2.

证明：（1）对任意的p1,p2,p3∈P,r∈R,p1≤p2,设f为l-R-模单同态，因为fg1(p1)=fg2(p3)，则有g1(p1)=g2(p3)，g1(r(p1+p3)) ≤g1(r(p2+p3))，g2(r(p1+p3)) ≤g2(r(p2+p3))，故g1=g2.反 之，若g1=g2，则g1(p1)=g2(p3)，因为fg1=fg2，有fg1(p1)=fg2(p3).故f为l-R-模单同态.

（2）设f是l-R-模满同态，ℎ1f=ℎ2f，但是ℎ1≠ℎ2，那么存在n∈N，ℎ1(n) ≠ℎ2(n).因为f是l-R-模满同态，存在m∈M,使f(m)=n.所以ℎ1f(m)=ℎ1(n)≠ℎ2(n)=ℎ2f(m).这与ℎ1f=ℎ2f矛盾.因此必有ℎ1=ℎ2.反之，假若f不是l-R-模满同态，Cokf=N/Imf≠0，取ℎ1是N到N/Imf的自然l-R-模同态，ℎ2是N到N/Imf的零同态，显然ℎ1≠ℎ2.任意的但ℎ1≠ℎ2，矛盾，因此f是满同态.

定理2.1设f:M→M′和g:M→N都是l-R-模同态，其中g是满同态并且Kerg⊆Kerf，则存在l-R-模同态ℎ:N→M′,使得f=ℎg.此外，Kerℎ=g(Kerf),Imℎ=Imf.所以ℎ是单的当且仅当Kerℎ=Kerf，ℎ是满的当且仅当f是满的.

证明：由于g是满的，对任意的元素n∈N,必存在m∈M，使得g(m)=n.如果又有m1∈M，使得g(m1)=n,则g(m-m1)=0，从而m-m1∈Kerg⊆Kerf,即f(m-m1)=0,f(m)=f(m1).因此，只要规定ℎ(n)=f(m)，就可定义一个同态映射ℎ:N→M′满足ℎg=f.下证交并同态.对于任意的n1,n2∈N，取m1,m2∈M，使得g(m1)=n1,g(m2)=n2，则对r1,r2∈R,有ℎ(r1m1∨r2m2)=f(r1m1∨r2m2)=r1f(m1)∨r2f(m2)=r1ℎ(n1)∨r2ℎ(n2),ℎ(r1m1∧r2m2)=f(r1m1∧r2m2)=r1f(m1)∧r2f(m2)=r1ℎ(n1)∧r2ℎ(n2).故ℎ 是l-R-模同态.

定理2.2设φ:M→N是l-R-模满同态，其中(M,+,≤)，(N,+,≤)是左R-模上Riesz空间，则

（1）Kerφ是M的凸子l-R-模；

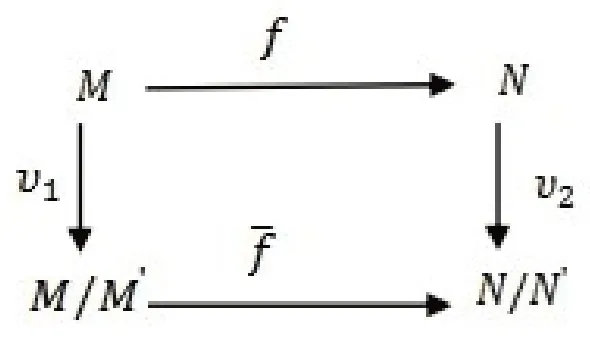
（2）若M′是M的一个凸子l-R-模，则M/M′是一个l-R-模，且自然映射ν:M→M/M′是l-R-模满同态；

（3）作为l-R-模M/Kerφ≅N.

证明：（1）首 先Kerφ是l-R-模M的一个子模,Kerφ=φ-1(0)={x∈M} .对任意的x,y∈Kerφ有φ(x∧y)=φ(x)∧φ(y)=0，故x∧y∈Kerφ，同理可得x∨y∈Kerφ，则(Kerφ,≤)是(M,≤)的子格；∀x,y,p∈Kerφ,∀r∈R(r≥0).当x≤y时,有rx≤ry，x+p≤y+p,因 此Kerφ是M的 子l-R-模；若∀x,y∈Kerφ,z∈M有x≤z≤y,可得z∈Kerφ，故Kerφ是M的凸子l-R-模.

（2）在M/M′={M′+x|x∈M} 中，定义M′+x≥M′+y的充要条件为存在s∈M′，使得s+x≥y，(M′+x)∨(M′+y)=M′+(x∨y)，(M′+x)∧(M′+y)=M′+(x∧y)，则M/M′是一个l-加群.由文献［2］知，对任意r∈R,M′+x∈M/M′,定义r(M′+x)=M′+rx，则M/M′是一个R-模.对任意的r∈R,(M′+x)∈(M/M′)+,存在s∈M′，使得s+x≥0，因为r(s+x)=rs+rx≥0，且rs∈M′，则r(M′+x)=M′+rx≥M′.任意的x1,x2,x3∈M，若M′+x1≥M′+x2，则 有因此M/M′是l-R-模.

对任意x∈M，因为ν(x)=M′+x，由文献［2］知ν是一个R模同态.对任意x∨y∈M，因为ν(x∨y)=M′+(x∨y)=(M′+x)∨(M′+y)=ν(x)∨ν(y)，同理ν(x∧y)=ν(x)∧ν(y).显然ν是满射，故ν是l-R-模满同态.

（3）由（1）（2）和定理2.1显然成立.

命题2.8设N和K是M的l-R-模，定义N+K={n+k|n∈N,k∈K}，则N+K是一个l-R-模.

证明：对任意N1，N2和K1，K2有(N1+K1)∨(N2+K2)=(n1+k1)∨(n2+k2)=(n1∨n2)+(k1∨k2)，(N1+K1)∧(N2+K2)=(n1+k1)∧(n2+k2)=(n1∧n2)+(k1∧k2)，其中n1,n2∈N，k1,k2∈K，则N+K是一个格.易知N+K对加法(N1+K1)+(N2+K2)=(n1+k1)+(n2+k2)=(n1+n2)+(k1+k2)可构成一个Abel加群，故N+K是一个l-加群.

由文献［2］可知，对任意的r∈R，n+k∈N+K，定义r(n+k)=rn+rk，则N+K是一个R模.对任意的r∈R+,n+k∈(N+K)+，则存在n1∈N,k1∈K，使得(n+k)+(n1+k1)=(n+n1)+(k+k1) ≥0，因 为r((n+k)+(n1+k1))=r(n+k)+r(n1+k1)=(rn+rk)+(rn1+rk1)=(rn+rn1)+(rk+rk1)≥0，且(rn+rn1)+(rk+rk1)∈N+K，则r(n+k)=rn+rk≥0，对任意n1,n2,n3∈N,k1,k2,k3∈K，若n1+k1≥n2+k2，则可得(n1+k1)+(n3+k3)=(n1+n3)+(k1+k3)≥(n2+n3)+(k2+k3)=(n2+k2)+(n3+k3)，因此N+K是一个l-R-模.

定理2.4设N和K都是M的凸子l-R-模，则K是N+K的凸子l-R-模，N∩K是N的凸子l-R-模，且(N+K)/K≅N/(N∩K).

证明：由文献［1］知，K是N+K的子模，对任意的k1,k2∈K，有k1∧k2=(0+k1)∧(0+k2)∈K,k1∨k2=(0+k1)∨(0+k2)∈K,故(K,≤)是(N+K,≤)的子格.∀r(＞0)∈R,k1,k2,k3∈K,若k1≤k2，则r(k1+k3)≤r(k2+k3)=rk2+rk3，则K是N+K的子l-R-模.任意的k1,k2∈K，n+k∈N+K，当k1≤n+k≤k2时，可得n+k=0+k=k∈K，因此可知K是N+K的凸子l-R-模.同理可得N∩K是N的凸子l-R-模.

设f:N→(N+K)/K，由文献［1］知，f是模同态，且f是满的.下证f是格同态.对任意的n1,n2∈N,有f(n1∨n2)=(n1∨n2)+K=(n1+K)∨(n1+K)=f(n1)∨f(n2),f(n1∧n2)=(n1∧n2)+K=(n1+K)∧(n1+K)=f(n1)∧f(n2).故f是l-R-模满同态.

若n∈Kerf,则f(n)=n+K=0,n∈K,但n∈N.故n∈N∩K.反之，设n∈N∩K，因为f(n)=n+K，而n∈K，则f(n)=K，即n∈Kerf.因此Kerf=N∩K，由定理2.2知(N+K)/K≅N/(N∩K).

定义2.4设θ是l-R-模M上的一个等价关系，对任意m,n∈M,m与n具有关系θ，记作m≡n(modθ).如果对任意的m,n,p,q∈M,r∈R,m≡p(modθ),n≡q(modθ)⇒m∨n(modθ)≡p∨q(modθ)且m∧n(modθ)≡p∧q(modθ),m+n≡(p+q)(modθ)，rm≡rp(modθ),则称θ是l-R-模M上的同余关系,对任意m∈M，m所在的等价类记作m/θ，即m/θ={n∈M|n≡m(modθ)}.则称M/θ={m/θ|m∈M}为M关于同余关系θ的商.

定理2.6设M是一个l-R-模,θ为M的一个同余关系，0 是M的零元，任意r∈R,令K=0/θ={m∈M|m≡0(modθ)}，则K是M的凸子l-R-模且对任意的m,n∈M,m≡n(modθ)⇔m-n∈K.反之，设K是M的一个凸子l-R-模，在M上规定一个二元关系θ:m≡n(modθ)⇔m-n∈K,则θ是M上的同余关系.

证明：（1）设θ是M上的一个同余关系，r∈R，令K=0/θ={m∈M|m≡0(modθ)}，由模论可知rm-0∈K，故rm≡0(modθ)，p∈M,m∈K，则p≡p(modθ)，m≡0(modθ)，-p≡-p(modθ)，从而p+m-p≡p+0-p(modθ)，即p+m-p≡0(modθ)，p+m-p∈K，且对任意m,n∈K,m≡0(modθ),n≡0(modθ),rm≡0(modθ),从而m∨n≡0 ∨0(modθ)≡0(modθ)，m∧n≡0 ∧0,(modθ)≡0(modθ),m+n≡0+0(modθ)≡0(modθ),-m≡0-m(modθ)≡(0-0)(modθ)=0(modθ)，从 而m+n,-m,rm,m∧n,m∨n∈K，对任意的r∈R+，当m∈K+，显然有rm≥0,rm∈K，所以K是M的l-R-子模.

对任意p∈M,m,n∈K，若m≤p≤n，则p∧m=m,p∧n=p,由m≡0(modθ)≡n(modθ)，有p∧m≡p∧n(modθ)，即m≡p(modθ)，从而p≡m(modθ)≡0(modθ)，从而p∈K，所以K是凸集，即K是M的凸l-R-子模.

对任意的m,n∈M，若m≡n(modθ)，则由-n≡-n(modθ)，m-n≡n-n(modθ)，即m-n≡0(modθ)，m-n∈K.反之，若m-n∈K，则m-n≡0(modθ)，m-n+n≡0+y(modθ)，即m≡n(modθ).

（2）设K是M的一个凸子l-R-模，在M上规定一个二元关系θ:m≡n(modθ)⇔m-n∈K.由模论可知θ是模M 上的同余关系,现设m,n,p,q∈K，则m-n∈K,p-q∈K,(m-n)∨(p-q)∈K,(m-n)∧(p-q)∈K，

从而(m-p)∧(n-q)≤m∧n-p∧q≤(m-p)∨(n-q).

因为K是凸的且(m-n)∨(p-q)∈K,(m-n)∧(p-q)∈K，所以m∧n-p∧q∈K，即m∧n≡p∧q(modθ).同样可证m∨n≡p∨q(modθ)，故θ是M上的同余关系.