二维随机格点伊辛模型中相变的蒙特卡罗模拟
2023-06-18周恒为黄以能
刘 洋,赵 薇,周恒为,黄以能
(伊犁师范大学物理科学与技术学院,新疆凝聚态相变与微结构实验室,新疆伊宁 835000)
0 引言
为了描述顺磁-铁磁相变,Lenz和Ising提出了现在一般称之为伊辛模型(Ising Model,IM)[1-3]的著名理论模型[4].IM的两个主要假设为:1)伊辛自旋(spin)假设,即自旋只能处于向上或向下两个状态,这里的自旋表示是材料晶体点阵上的原子、分子、离子中电子的自旋磁矩和轨道磁矩的总磁矩,准确地说是赝自旋(Pseudo-spin),一般简称为自旋[5];2)最近邻相互作用假设,即晶体点阵上的自旋,只有在最近邻的情况下,才存在相互作用.后来的研究表明,IM模型也是描述顺电-铁电相变最为成功的模型[6].
Klein-Brout提出的长程相互作用随机格点(random-site)伊辛自旋模型[7],是为了描述磁性金属固溶体材料(CuφMn1-φ、AuφFe1-φ等)而提出的.Klein-Brout 模型的3 个主要假设为:1)自旋和自旋空位(spin vacant)假设,即晶体点阵的任一格点上由自旋(如AuφFe1-φ中的Fe原子)或自旋空位占据,自旋空位定义为无自旋或自旋为0(如AuφFe1-φ中的Au原子);2)点阵上自旋随机分布假设,即在保证每个点阵格点上的平均浓度为1-φ条件下,自旋在点阵上随机分布;3)自旋之间长程相互作用假设,即模型体系中,任意一对自旋之间的相互作用为RKKY势[8-10].
Binder等[5]用IM的最近邻自旋相互作用假设,对Klein-Brout模型的长程相互作用进行简化,即得到现在一般所谓的随机格点伊辛模型(random-site-IM,RSIM).Zhang-Huang[6]发现,在RSIM中再引入随机场(random-field,RF),即RFRSIM,可以对弛豫铁电性(relaxor-ferroelectricity)进行较好的描述.
目前,虽然已经获得一维RSIM(1D-RSIM)体系热平衡态的精确解,但是2D-RSIM、3D-RSIM仍未获得相应的精确解[5,6].已有的蒙特卡罗(Monte Carlo,MC)模拟结果[11-14],则存在所模拟的自旋空位浓度φ点既不够多、系统性也不够足等问题.针对该问题,本文用MC方法[15],对2D-RSIM体系的比热随温度变化,特别是所表现的相变行为,随φ的演化,进行了细致的计算机模拟.
1 二维随机格点伊辛模型与蒙特卡罗方法介绍
2D-RSIM模型的哈密顿量H为
其中,σi,j表示二维点阵中第i行第j列格点上的自旋,σi,j=1或-1,表示自旋的状态;J为最近邻自旋之间的相互作用能常数;φ为自旋空位浓度(0 <φ≤1);r是0到1之间的随机数;ri,j为随机函数,当r<φ时=0;r≥φ时=1;n为沿着晶轴方向的自旋数目;n→∞表示热力学极限(thermodynamic limit);μ0为真空磁导率;μ为自旋磁矩.对伊辛自旋体系,H就是体系中任意一个自旋取1或-1的自旋构型(spin configuration)的能量.
另外,上述自旋体系处于可以交换能量的温度为T的热浴(heat bath)中,即自旋体系和热浴共同构成一个正则系综(canonical ensemble).
当模型体系处于热平衡时,基于Boltzmann-Gibbs 统计得,体系中单个自旋的平均内能U、平均比热C为
将方程(3A)(3B)(3C)代入方程(2B),原则上可以严格计算2D-RSIM的热平衡态的C,但是如上文所述,迄今为止仍然未获得其精确解.
MC模拟是一种以概率和统计理论为基础,用计算机实现统计抽样,以获得问题近似解的方法.下文具体介绍利用MC方法,对2D-RSIM体系中,晶体点阵、点阵上自旋随机分布、体系中自旋翻转、体系的热平衡自旋构型、体系的C等模拟过程.
因为热力学实际系统包含巨大的粒子数,所以往往可以看作是一个无限大的系统.但是当进行模拟时,因为计算机内存和运行时间的限制,只能选择有限体系.本文选择模拟2D-RSIM体系中所包含的自旋数目n2(1-φ)=2002.由于有限体系必然存在边界,本文选用的是自由性边界条件,即边界上自旋与模拟体系之外不存在相互作用.
二维正方点阵的模拟:生成晶格常数为a、原胞数目为n×n的二维正方点阵,如图1所示.

图1 二维随机格点伊辛模型(2D-RSIM)示意图(空位浓度φ=0.3),其中蓝色实线表示正方点阵,红色圆点表示自旋
点阵上随机自旋的模拟:对应每个格点位置,生成0至1之间的随机数r,若r≥φ,则在格点上模拟放置自旋;若r<φ,表示没有自旋(如图1).
自旋翻转的模拟:本文选择自旋翻转的Glauber 动力学[5,6,16],即自旋构型的变化由单个自旋的翻转导致,并且单个自旋翻转概率(自旋每次尝试翻转过程中,实现由σi,j向-σi,j翻转的概率)为
其中,Fi,j为σi,j的局域场:
由于不同文献中对Markov过程[15]的一个MC步(MC Step)的表述不尽相同,本文选择的一个MC步过程为:对图1所示的2D-RSIM体系中每个自旋,依次使用自旋翻转的Glauber动力学(方程4),即利用MATLAB的随机数函数产生0到1之间的随机数r;当p>r时,自旋发生偏转;当p≤r时,自旋不发生偏转.
热平衡自旋构型的模拟:本文选择自旋全部向上的自旋构型为模拟的初始构型,即σi,j=1.体系每经过一个MC步后,一般会得到一个新的自旋构型,对第k步体系的一个确定自旋构型的能量为
因为本文模拟的系综是正则系综,所以选择随MC步数变化的Hk作为热平衡的判据参量,即一定的MC步数内Hk的平均值,基本不随MC 步数变化,就认为模拟体系趋于温度为T的热平衡态.如图2 所示,当φ=0.0 时,对T=2.50J=1.11Tc(Tc将在下文讨论),k>102步以后,Hk的平均值基本不随k变化,即可以认为体系趋于热平衡态;对T=2.26J=1.00Tc,当k>103步以后,体系趋于热平衡态;对T=2.03J=0.90Tc,T=1.83J=0.81Tc,T=1.42J=0.63Tc,当k>20步以后,体系趋于热平衡态.
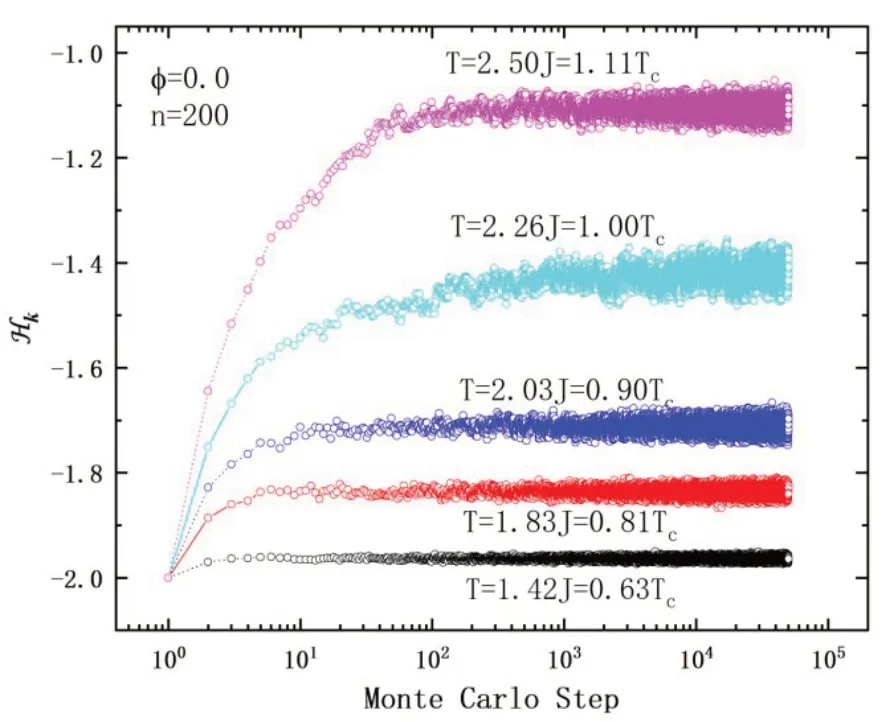
图2 系列温度(T)下,蒙特卡罗模拟的二维随机格点伊辛模型(2D-RSIM)(自旋空位浓度φ=0.0)的能量(Hk)随蒙特卡罗步数的变化结果
图3的相应模拟结果表明,对不同的φ,当T=0.81Tc时,k>103以后,体系基本都趋于热平衡态.

图3 特定约化温度(T Tc=0.81,Tc为相变温度)下,蒙特卡罗模拟的系列自旋空位浓度φ的二维随机格点伊辛模型(2D-RSIM)的能量(Hk)随蒙特卡罗步数的变化结果
由于本文重点模拟2D-RSIM的相变特征,即研究温区主要在Tc附近,k>103步后认为体系基本趋于热平衡是可行的.但是,考虑到不同φ以及不同T下,体系到达热平衡所需的MC步数不同,步数越大模拟结果会越好.因此本文选择的到达热平衡的MC步数(kE)为50 000步,总的MC步数(kF)为150 000.
2 模拟结果与分析讨论
图4为系列自旋空位浓度φ、自旋数目为n×n的2D-RSIM中,单个自旋的平均比热C随温度T变化的计算机模拟结果.当φ=0.0时,2D-RSIM简化为2D-伊辛模型(2D-IM).由于2D-IM的C的精确解已经由昂萨格(Onsager)给出[3,17],这里作为验证本文模拟结果的依据.首先,C的精确解表明,2D-IM的相变温度Tc=2.27J,本文的模拟结果Tc=2.26J(图4a),比精确解低0.44%,微小的偏差源于本文模拟的是n×n=200×200的有限体系的边界效应;其次,C的精确解还表明,其在Tc附近对数发散,即C∝-ln| |T-Tc,除去极为靠近Tc点C值较小外,本文的模拟结果也给出了基本相同的结果(图4a).因此,本文对2D-IM的计算机MC模拟结果(方程4-6)与精确解结果(方程2-3)偏差较小,可以预期本文对2D-RSIM的模拟结果也具有较高的可信度.

图4 系列自旋空位浓度φ、自旋数目为n× n的2D-RSIM中,单个自旋的平均比热C随温度T变化的计算机模拟所得结果.其中,黑线:φ=0.0,n →∞的精确解;红色圆点:φ=0.0,n×n=200×200;蓝色圆点:φ=0.1,n×n=211×211;洋红色圆点:φ=0.2,n×n=224×224;海军蓝色圆点:φ=0.3,n× n=239×239;紫色圆点:φ=0.4,n× n=258×258;橄榄绿色圆点:φ=0.5,n× n=283×283;深青色圆点:φ=0.6,n× n=316×316;皇家蓝圆点:φ=0.7,n× n=365×365;橙色圆点:φ=0.8,n× n=447×447;紫罗兰圆点:φ=0.9,n× n=633×633
图4的结果还表明,对所有的φ值,C随着T变化明显存在一个峰,并且随着φ变大,峰形由尖锐变得越来越圆滑,并且在不断变宽.虽然按照早期的Ehrenfest相变分类法[18],圆滑的比热峰表示体系中不存在相变;但是随着研究的深入,尽管仍然存在争议[19,20],现在一般认为体系中发生了弥散相变(diffuse phase transi‐tion)[6]或者初始相变(incipient phase transition)[19].
本文作者认为2D-RSIM中发生了弥散相变,并将C的峰值对应的温度称为相变温度Tc(图4a).由图5可见,Tc随φ的增大总体上单调降低,细致分析则可以发现存在3 个Tc随φ线性变化的区域(I 区、II 区、III区),其中I区下降斜率最大,III区下降斜率最小.上述Tc随φ变化的3个线性区域是本文首次发现,对应的微观机制仍需深入研究.

图5 计算机模拟所得的二维随机格点伊辛模型(2D-RSIM)的相变温度Tc随自旋空位浓度φ的变化结果
