相对连续偏序集及其应用

刘东明，姜广浩，李 辉

（淮北师范大学数学科学学院，安徽淮北235000）

1 引言与预备知识

由于计算机程序语言逻辑的迫切需要，著名数学家Scott于1972年首次引入连续格的概念，并由此创建了比较完整的连续格理论[1].随后相关学者将连续格理论推广到使用更广泛的连续Domain[2]上.Domain理论的一个重要的研究方向是将其推广到一般的偏序集中去，如，连续偏序集[3-5]、拟连续偏序集[6-7]、C-连续偏序集[8-9]等.本文在以往文献的基础上，将定向集和一致集进行推广.首先引入相对定向集和相对定向完备集的概念，并在相对定向完备集上引入相对双小于的概念，研究其在给定的集合T中的一些性质；然后利用相对way below关系引入相对连续偏序集的概念，探讨了它的一些等价条件；最后引入相对遗传性的概念，证明了相对连续偏序集在给定的集合T下具有相对T的遗传性.

设P为偏序集，∀X⊆P，记↓X={y∈P：∃x∈X，y≤x}，对偶地，记↑X={y∈P：∃x∈X，x≤y}，并记↓x=↓{x}，↑x=↑{x}.设P为偏序集，X⊆P，则X是下集当且仅当X=↓X，X为上集当且仅当X=↑X.若∀x、y∈X，∃z∈X，使得 x、y≤z，则称 X是P的定向集.对偶地，可以定义余定向集.

定义1[2]设P为偏序集，X⊆P，称X为理想，当且仅当X既是下集又是定向集.对偶地，可以定义滤子.记P的所有理想构成的集合为Idl（P），P的所有滤子构成的集合为Filt（P）.

定义2[2]设P为偏序集，若对于任意定向子集D，sup D存在且sup D∈D，则称偏序集P是定向完备的，简记为DCPO.

定义3[4]设P为偏序集，S⊆P，若∀x、y∈S，存在z∈P，使得 x≤z，y≤z，则称 S 为 P 的一致集.

定义4[4]设P为偏序集，若对于任意一致集S，sup S存在且sup S∈S，则称偏序集P为一致完备的，简记为UCPO.

定义5[4]设P为偏序集，定义P上的waybelow＜＜u关系如下：∀x、y∈P，若对于任意一致集S，当y≤sup S时，存在s∈S，使得x≤s，则称x一致小于 y，记作x＜＜uy.记⇓ux={v：v＜＜ux}.

定义6[4]设P为一致完备偏序集，若对于任意x∈P，x=sup⇓ux，则称P是一致连续偏序集.

定义7设P为偏序集，S、T⊆P，S≠，T≠，若∀x、y∈S，存在 t∈T，使得 x≤t，y≤t，则称 S 为偏序集P相对于T的定向集.当T明了时，简称S为相对定向集.

例1设P为偏序集，T⊆P，T≠，∀x∈T，则单点集{x}是P中相对于T的定向集.

定义8设P为偏序集，T⊆P，T≠，若任意相对于T的定向集都存在最小上界，则称P为相对于T的定向完备集.当T明了时，简称P为相对定向完备集，简记为 RDCPO（T）.

设P为偏序集，且P具有性质Q，若P的任意非空子集也具有性质Q，则称Q在P中具有遗传性.

2 相对way below关系

定义9设P为相对于T的定向完备集，定义P上的相对 way below＜＜T关系如下：∀x、y∈P，若对于任意相对于T的定向集S，当y≤sup S时，存在s∈S，使得x≤s，则称x在P上相对于T小于y，当T明了时，简称 x相对小于 y，记为 x＜＜Ty.若 x＜＜Tx成立，则称x为P上相对于T的紧元，当T明了时，简称x为相对紧元.记⇑Tx={u：x＜＜Tu}，⇓Tx={v：v＜＜Tx}.

命题设P为偏序集，T⊆P，T≠，若P为相对于T的定向完备集，则对于任意u、x、y、z∈T，有如下结论成立.

（1）x＜＜Ty⇒x≤y.

（2）u≤x＜＜Ty≤z⇒u＜＜Tz.

（3）⇓Tx∈U（T）.

（4）当P有最小元0时，0＜＜Tx.

（5）x＜＜Tz，y＜＜Tz，若 x∨y存在，则 x∨y＜＜Tz.

证明（1）∀D∈U（T），由于P为相对于T的定向完备集，则sup D存在，若y≤sup D，则存在d∈D，使得 x≤d，取 D={y}∈U（T），则 x≤sup D=y.

（2）∀D∈U（T），sup D存在，若 z≤sup D，由条件得y≤sup D，又 x＜＜Ty，从而存在 d∈D，使得 x≤d，又因为 u≤x，所以u≤d，由相对way below的定义得u＜＜Tz.

（3）∀a、b∈⇓Tx，有 a＜＜Tx 且 b＜＜Tx，则 a≤x，b≤x，而 x∈T，所以⇓Tx∈U（T）.

（4）∀D∈U（T），若 x≤sup D，则存在 d∈D，使得x≤d，又由于0是P的最小元，故0≤d，所以0＜＜Tx.

（5）∀D∈U（T），则 sup D 存在且 sup D∈D，若z≤sup D，因为 x＜＜Tz，y＜＜Tz，故存在 d1、d2∈D，使得x≤d1≤sup D 且 y≤d2≤sup D，进而 x∨y≤sup D，所以x∨y＜＜Tz.

由命题易得推论1和推论2.

推论1设P为偏序集，T⊆P，T≠，若P为相对于T的定向完备集，则∀x∈T，有⇓Tx⊆↓x，⇑Tx⊆↑x.

推论2设P为偏序集，T⊆P，T≠，若P为相对于T的定向完备集，则∀x、y∈T且x≤y，有⇓Tx⊆⇓Ty.

推论3设P为偏序集，T⊆P，T≠，若P为相对于T的定向完备集，x∈T，则有⇓Tx∈RId（lT）.

证明由命题的（3）知⇓Tx∈U（T），下证⇓Tx为下集.任意取 a∈⇓Tx，则 a＜＜Tx，任意取 b∈P，若 b≤a，再由命题的（2）得 b＜＜Tx，因此⇓Tx为下集，故⇓Tx∈RId（lT）.

引理设P为偏序集，T⊆P，T≠，则I（rT）⊆U（T）.

证明∀M∈I（rT），则存在S∈U（T），使得M=↓S.∀x、y∈M，则有 x、y∈↓S，从而存在 s1、s2∈S，使得x≤s1，y≤s2，又 S 为相对于 T 的定向集，故存在 t∈T，使得 s1≤t，s2≤t，进而有 x≤t，y≤t，所以 M 为相对于T的定向集.

定理1设P为偏序集，T⊆P，T≠，P为相对于T的定向完备集.∀x、y∈T，x＜＜Ty当且仅当∀I∈I（rT），若 y≤sup I，则 x∈I.

证明必要性 ∀I∈I（rT），由引理得I⊆U（T），故I相对于T定向且为下集，若x＜＜Ty且y≤sup I，则存在d∈I，使得x≤d，进而x∈I.

充分性 ∀I∈I（rT），有I∈RId（lT），对于任意x∈I，则存在d∈I，使得x≤d，即对于任意相对于T定向的I，若y≤sup I，则存在d∈I，使得x≤d，故有x＜＜Ty.

定理2设P为一致完备集，T⊆P，T，∀x∈T，则有⇓ux⊆⇓Tx.

证明∀a∈⇓ux，有 a＜＜ux，下证 a∈⇓Tx，任意取D⊆U（T），则D为P中的一致集，因为P为一致完备集，所以sup D存在，若x≤sup D，则存在d∈D，使得a≤d，由相对way below关系的定义得a＜＜Tx，从而a∈⇓Tx，故⇓ux⊆⇓Tx.

3 相对连续偏序集

定义10设P为偏序集，T⊆P，T≠，且P为相对于T的定向完备集，若∀x∈T，x=sup⇓Tx，则称P为相对于T的连续偏序集.当T明了时，简称P为相对连续偏序集.

注1相对连续偏序集未必为一致连续偏序集.

例2设偏序集 P=M∪N，见图 1.N={a，b，c，d}，规定P的序：若x、y∈M，则x≤y当且仅当x=y；若x∈N，y∈M,则 x≤y；若 x、y∈N，N 上的序如图 1所示.令T={b，c，d}，则P为相对于T的连续偏序集.然而，对于一致集N，sup N∉N，P不为一致完备集，从而P不是一致连续偏序集.

图1 偏序集P=M∪NFig.1 Poset P=M∪N

注2相对连续偏序集未必为连续偏序集，连续偏序集也未必为相对连续偏序集.

例3设 P=[0，1），T=[0，1/2]，则 P 为相对于T的连续偏序集，但由sup P∉P知P不为定向完备偏序集，故P不为连续偏序集.

定理3设P为一致连续偏序集，则∀T⊆P，T≠，P为相对于T的连续偏序集.

证明若P为一致连续偏序集，则P为一致完备集，从而P为相对于T的定向完备集.∀x∈T，由定理1知⇓Tx∈U（T）.下证x=sup⇓Tx.首先，易知x为⇓Tx的一个上界，从而sup⇓Tx≤x；其次，由定理2得⇓ux⊆⇓Tx，又P为一致连续偏序集，故有x=sup⇓ux≤sup⇓Tx，进而x=sup⇓Tx.所以P为相对于T的连续偏序集.

定理4设P为偏序集，T1⊆T2⊆P，T1、T2≠，若P为相对于T2的连续偏序集，则P为相对于T1的连续偏序集.

证明设P为相对于T2的连续偏序集，则P为相对于T2的定向完备集.首先证P为相对于T1的定向完备集.∀D∈U（T1），∀a、b∈D，存在 t∈T1⊆T2，使得a≤t且b≤t，从而 D∈U（T2），又P为相对于 T2的定向完备集，故sup D存在且sup D∈D，进而P为相对于T1的定向完备集.∀x∈T1，由定理1知.下面证易知的一个上界，从而下证，则有，，有，因P为相对于T1的定向完备集，故sup D存在且sup D∈D，若 x≤sup D，又，故存在 d∈D，使得y≤d，由相对way below的定义可知，进而，所以，又因P为相对于T2的连续偏序集，进而有，故综上可知P为相对于T1的连续偏序集.

定义11设P为偏序集，T⊆P，T≠，若P具有性质Q，且T中的任意子集D都具有性质Q，则称Q在P中具有相对于T的遗传性.当T明了时，简称相对遗传性.

注3若某种性质具有遗传性，则必具有相对遗传性.

注4若某种性质具有相对遗传性，则未必具有遗传性.

例4设偏序集 P={a，b，c，d，e，f}，见图 2.设T={b，d，e}，易知P为定向的，且对于任意T中的非空子集D，D都是定向的，但显然P中的子集不都是定向的.故定向性质具有相对于T的遗传性，但不具有遗传性.

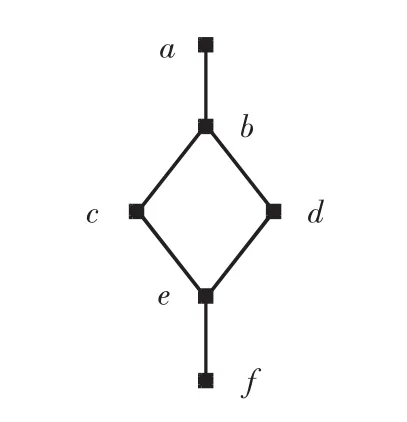
图2 偏序集 P={a，b，c，d，e，f}Fig.2 Poset P={a，b，c，d，e，f}

定理5设P为相对于T的连续偏序集，T⊆P，T≠，则对于T的任一非空子集D，P为相对于D的连续偏序集.