基于复合泊松过程与时间序列模型的新疆森林火灾特征预测分析研究

王 瑶，卢芸潇，刘 淼，2*

（1.伊犁师范大学数学与统计学院，新疆伊宁 835000；2.伊犁师范大学应用数学研究所，新疆伊宁 835000）

0 引言

新疆位于我国西北边疆，是我国荒漠面积最大、生态环境较为脆弱的地区；同时也是我国森林资源较少的省区之一，并且林地面积小、结构不合理、分布不均匀.火灾干扰在新疆的生态系统中起着主导作用，改变了森林演替、生物地球化学循环和碳存储.

寻找统计模型来描述这一地理区域火灾和燃烧面积的年数趋势是森林科学家非常感兴趣的问题.事实上，对这些模型的详细分析可能会揭示火灾发生模式的新方面，并就火灾机理提出重要的想法.有几种统计方法可以根据火灾数据揭示前兆地震活动.曼达拉兹和Ye发现了泊松概率模型，很好地描述了森林野火燃烧的过程［1-2］.本文提出简单的泊松模型，作为模拟野火发生的随机性的一种实用方法；还利用复合泊松模型对大火灾造成的损害进行了火灾的总烧毁面积的建模；并通过二重复合泊松过程对新疆森林火灾造成的经济损失进行描述，希望所得结果对相关部门今后掌握新疆森林火灾的变化规律提供一定的借鉴与参考.

1 时间序列分析

1.1 基本概念

1.1.1 时间序列

时间序列是指某一现象的统计指标值按时间顺序所排列的数据，时间序列分析方法用于确定时间序列的周期、趋势和概率结构.基于该结构建立的模型通常用于模拟隐含在时间序列中的过程，从而对未来进行预测，用于解决实际问题.

1.1.2ARIMA模型简介

ARIMA(p,d,q)（简称ARIMA模型）全称为差分自回归移动平均模型（Autoregressive Integrated Moving Average Model），是由博克斯（Box）和詹金斯（Jenkins）于20世纪70年代初提出的一种著名的时间序列预测方法，所以又称为Box-Jenkins模型、博克斯-詹金斯法.ARIMA模型是指将非平稳时间序列转化为平稳时间序列，然后将因变量仅对它的滞后值，以及随机误差项的现值和滞后值进行回归所建立的模型［3］.

ARIMA模型是自回归模型（AR模型）和移动平均模型（MA模型）的混合模型.其中，p为自回归项；q为移动平均项；d为时间序列变成平稳时间序列时所做的差分次数.本文所使用的是非季节性的ARIMA模型，即

或简写为

其中，B为后移算子；∇d为向后差分算子；φ(B)=1-φ1B-φ2B2-...-φpBp为自回归算子；θ(B)=1-θ1B-θ2B2-...-θqBq为移动平均算子［4］.

1.2 新疆森林烧毁面积的ARIMA模型

1.2.1 新疆森林烧毁面积的数据初步判断

本文就表1 所示的2003～2019 年新疆森林火灾年度烧毁面积［5］，建立新疆森林火灾烧毁面积的ARIMA(p,d,q)模型.

表1 2003～2019新疆森林火灾数据

利用SPSS软件对新疆2003～2019年的森林火灾烧毁面积的数据进行分析.

图1为2003～2019年新疆森林火灾烧毁面积的时间序列图.

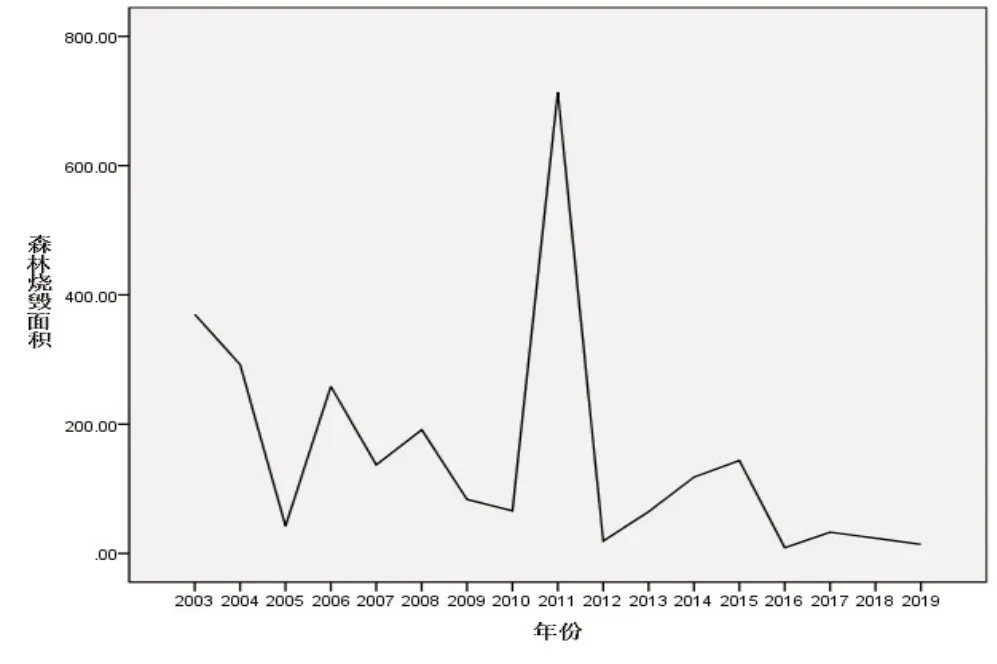
图1 2003～2019年新疆森林火灾烧毁面积序列图

从图1中可以看出，2003～2019年新疆森林火灾烧毁面积的序列图是一个非平稳时间序列.本文对数据作二阶差分后得到一个平稳的时间序列，见图2.由图2可以看出对原始序列作二阶差分能使该时间序列基本达到平稳状态.

图2 二阶差分后的时间序列图

1.2.2 模型的识别与定阶

利用ACF图、PACF图与贝叶斯信息准则（Bayesian Information Criterions，BIC）确定模型的阶数，采用最大似然估计或最小二乘的方法对识别阶段提供的模型进行参数估计，并假设检验，用以判断模型是否恰当［6］.利用统计软件绘制自相关图及偏相关图（见图3、图4），进行阶数的初步判断.

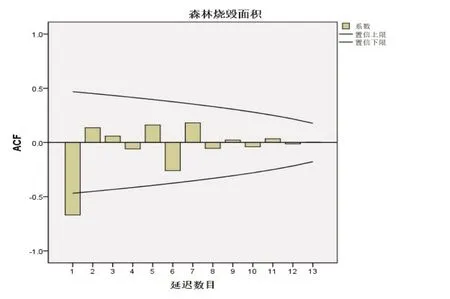
图3 二阶差分后的自相关图

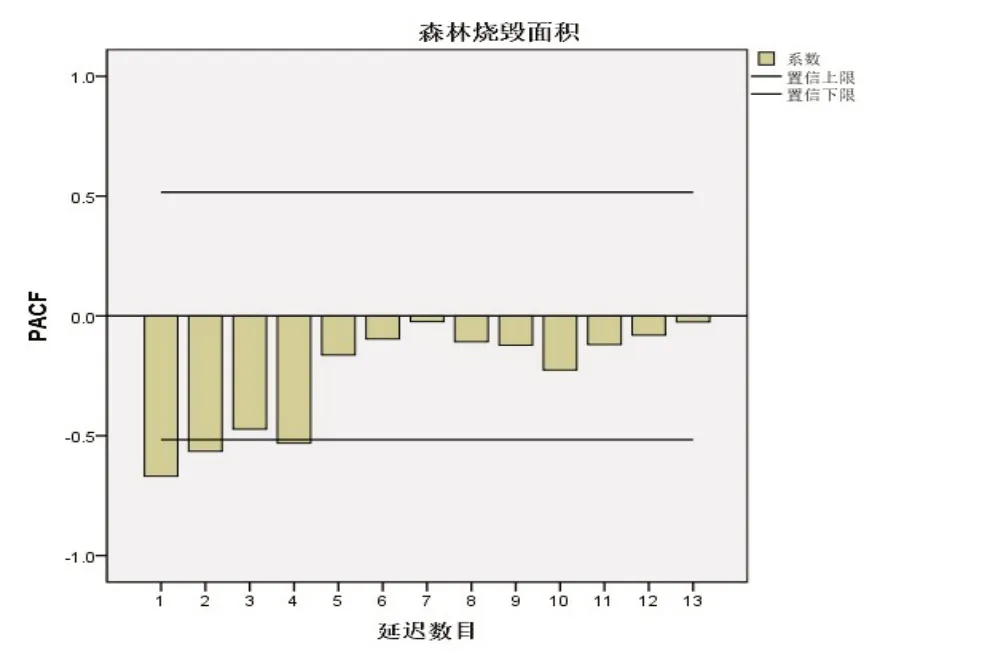
图4 二阶差分后的偏相关图

对该时间序列取不同参数值来比较BIC值（BIC值越小越好），以及比较平稳的R2值和MAE值，反复拟合取(p,d,q)=(2,2,0)时，时间序列模型的BIC值达到最小值12.113，R2=0.611，模型拟合效果比较显著.

1.2.3 模型的参数估计

取(p,d,q)=(2,2,0)时，模型的参数估计结果如表2所示.由表2可以看出，回归系数的p值都小于0.05，接近于0，于是得到结论：t检验效果显著.

表2 参数估计值

1.2.4 模型的显著性检验

模型的显著性检验是对序列的原始数据与拟合数据的误差序列进行相关检验，看其是否与实际相吻合，是否能够很好地反映实际，对时间序列模型的检验即就是看残差序列是否为白噪声序列［7］.本文检验是否为白噪声序列的方法选择观测残差序列的ACF图和PACF图进行检验，见图5.

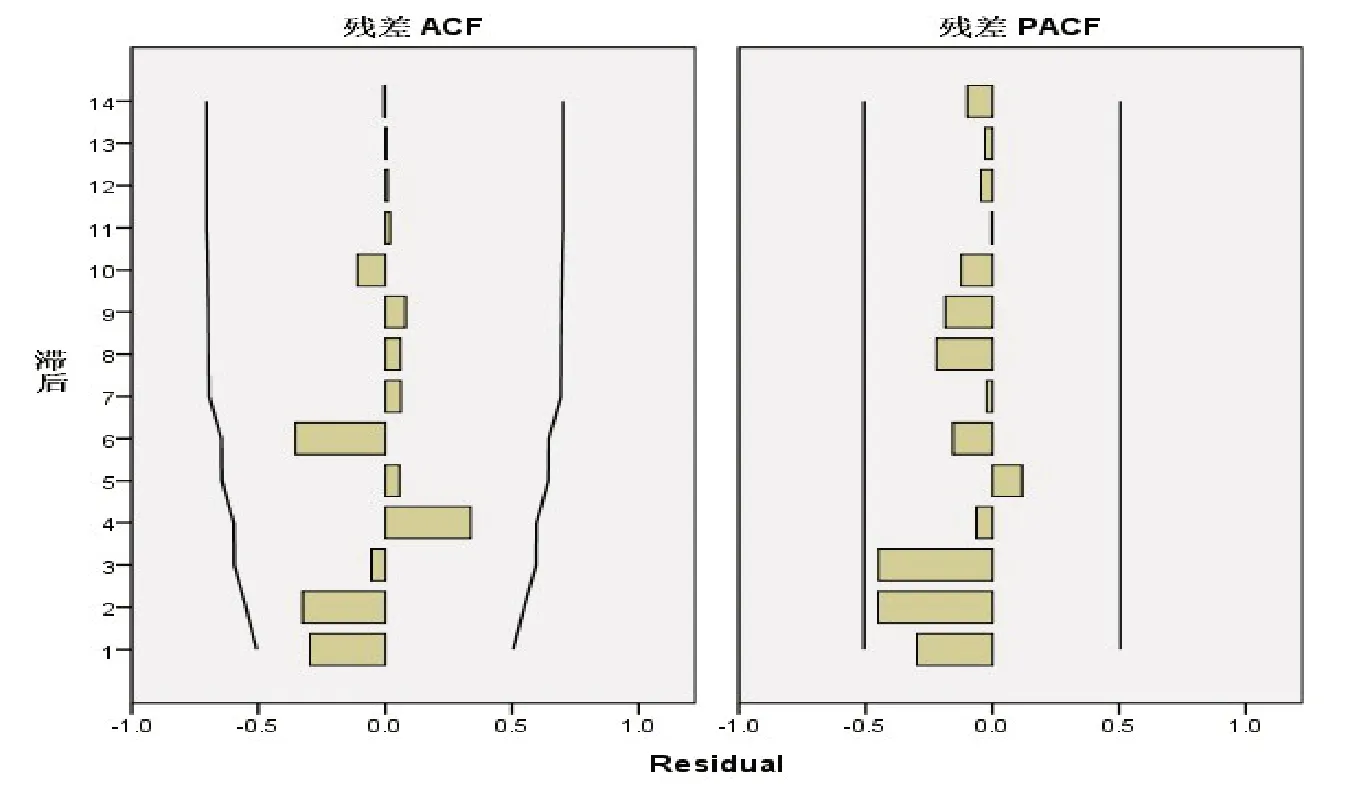
图5 ARIMA模型残差的相关函数图

由图5可知，残差的ACF和PACF都是平稳的，两者的数值都趋向于0，但都不等于0，并且残差序列数值之间没有相关性.因此残差序列近似为白噪声序列.于是得到的模型ARIMA(2,2,0)能够较好地用来拟合新疆2003～2019年森林火灾烧毁面积的时间序列.

1.2.5ARIMA(2,2,0)模型的预测

利用建立的模型预测新疆森林火灾烧毁面积，得到预测值与实际值的对比结果，如图6：

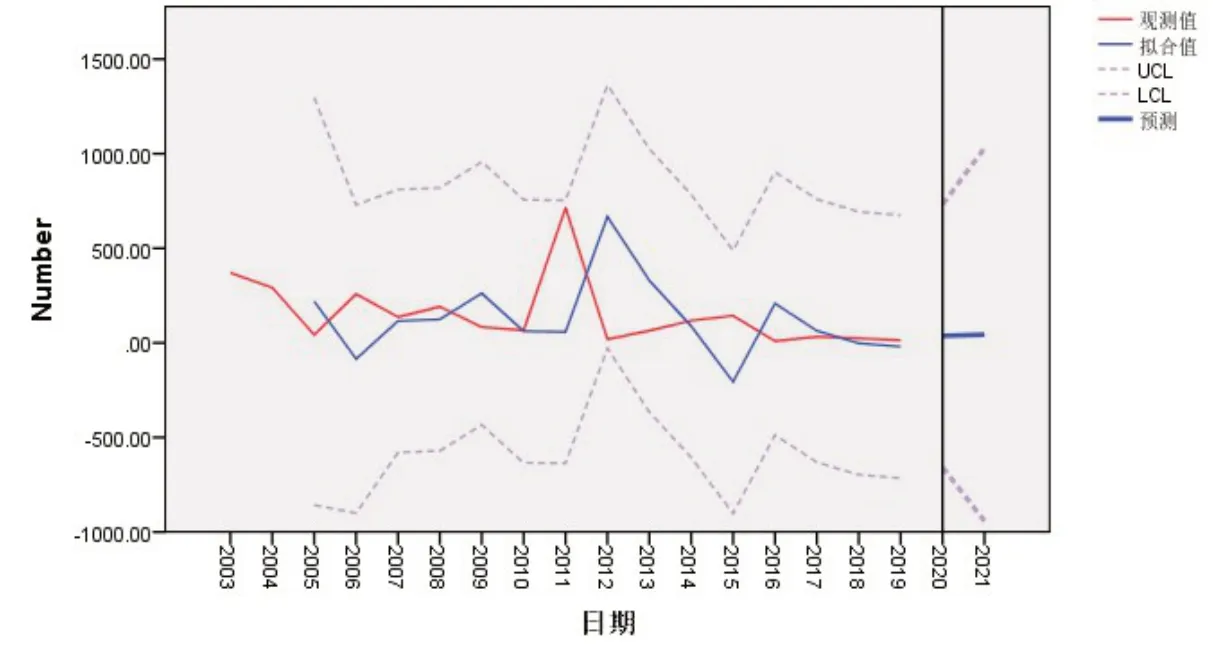
图6 新疆森林火灾燃烧面积预测值与实际值对比图

对比图6中的原始序列和实际序列，模型的预测是合适的.使用该模型对未来两年（2020～2021年）新疆森林火灾烧毁面积进行预测，结果如表3 所示.由表3 预测得到2020 年新疆森林火灾烧毁的面积约为37.57 hm2；预测2021年新疆森林火灾所致的烧毁面积约为43.82 hm2.

表3 新疆2020～2021年森林火灾烧毁面积预测值

2 复合泊松过程

2.1 预备知识

定义1［8］称计数过程{N(t),t≥0}，为具有参数λ＞0的泊松过程，如果{N(t),t≥0} 满足下列条件：

（1）N(0)=0；

（2）N(t)是独立平稳增量过程；

（3）P{N(h)=1}=λh+o(h)；

（4）P{N(h)≥2}=o(h).

定义2［9］设{N(t),t≥0} 是参数为λ的泊松过程，若其中{Xn,n=1,2,...} 为独立同分布随机变量序列且与{N(t),t≥0} 独立，则称{Y(t),t≥0} 为复合泊松过程.

定义3［10］若{Y(t),t≥0} 是一复合泊松过程，{ηn,n=1,2,...} 是独立同分布的非负整数值随机变量序列，且{ηn} 与{Y(t)}相互独立.令,t≥0，则称{Z(t),t≥0} 为二重复合泊松过程.

2.2 主要结论

定理1若{N(t),t≥0} 是参数为λ的泊松过程，且E(X12)＜∞，则复合泊松过程,t≥0的基本数字特征如下：

（1）特征函数为gY(t)(u)=exp{λt[gX(u)-1]}，其中gX(u)是随机变量X1的特征函数，λ表示速率；

（2）均值函数为E[Y(t)]=λtE(X1)；

（3）方差函数为D[Y(t)]=λtE(X12).

由于{N(t)≥0,t≥0} 与{Xn,n=1,2,...}，是相互独立的，则

（2）根据特征函数与矩的关系得到数学期望为

（3）均方值为

于是Y(t)的概率生成函数为

若s=0，gY(t)(s)的k阶导数如下：

当m=1，x=0,1 且n=1,2,...时，P(Xn=0)=p0，P(Xn=1)=1-p0，此时易见Y(t)是参数为λ(1-p0)t的泊松过程.

当m=2时，Y(t)的概率生成函数为

当m＞2时，利用上述同样的方法进行微分及代数运算，得到m＞2的概率

通过归纳得

2.3 实证分析

2.3.1 模型的建立

从《新疆统计年鉴》中收集到2003～2019年有关新疆森林火灾的数据如图7.

图7 2003～2019年新疆森林火灾发生次数

利用图7 中的数据进行分析.令{N(t),t≥0} 为某一给定季节内新疆地区森林火灾发生次数的齐次泊松过程，则相应的森林火灾的烧毁面积Xn,n=1,2,...为独立同分布随机变量，且与{N(t),t≥0} 独立，则在[0,t]时间段内，新疆森林火灾烧毁的总面积可看作一个复合泊松过程Y(t)=X1+X2+...+XN(t)=当每次新疆地区森林火灾燃烧面积相互独立时，即可确定新疆森林火灾烧毁总面积的概率密度函数.在t时间段内新疆森林火灾造成的经济损失可看成一个二重复合泊松过程.当每一单位面积烧毁造成的经济损失相互独立时，便可得到新疆森林火灾造成总经济损失的数学模型.

2.3.2 模型检验

本文利用Kolmogoroν‐Smirnoν检验统计量(ρ=0.095)，得到{N(t),t≥0} 是一个齐次泊松过程，λ=36.88（年），这意味着每年新疆森林火灾预期达到36.88次.从图8和Kolmogoroν-Smirnoν检验中得到了新疆森林火灾燃烧面积的频率分布，随机变量Xn,n=1,2,...为对数正态分布.根据Spearman-ρ检验（Spearman-ρ=0.204；p=0.433），满足独立性假设条件.因此得到是一个复合泊松过程.利用随机变量Xn与N(t)的分布特性同样可得新疆森林火灾烧毁总面积的复合泊松过程的概率函数.

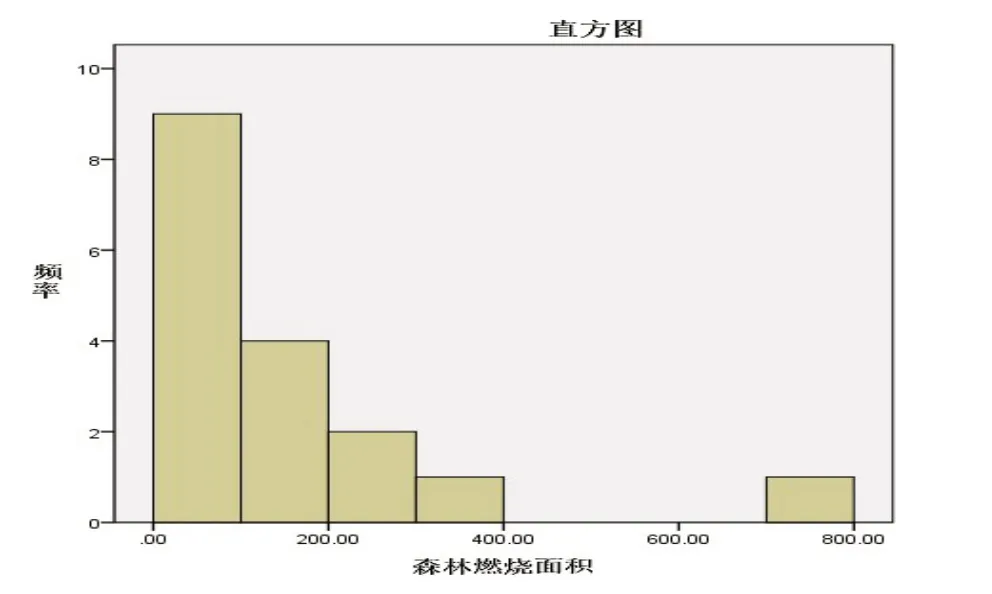
图8 新疆森林年度燃烧面积图

通过Kolmogoroν-Smirnoν检验得到随机变量ηn,n=1,2,...为一个正态分布.根据Spearman-ρ检验（Spearman-ρ=0.074；p=0.859），我们接受独立性假设.因此我们认为是一个二重复合泊松过程.

3 结束语

本文首先介绍了一种时间序列模型，用于对新疆未来两年森林火灾的燃烧面积进行预测；同时提出了一种复合泊松模型，用于模拟给定季节内新疆森林火灾的年度燃烧面积和火灾次数的分布.利用新疆2003～2019年森林火灾的历史数据来拟合模型，最后得到新疆森林火灾燃烧总面积的复合泊松过程的数字模型和新疆森林火灾所造成经济损失的二重复合泊松过程的数学模型，从而说明建立复合泊松模型，可以很好地对新疆森林火灾燃烧总面积和燃烧次数进行概率拟合.本研究中得到的新疆森林火灾的分布规律对于未来相关部门防控和管理新疆森林火灾系统有一定的参考价值.