优化解题方法,培养理性思维
2023-06-16陈国祥
陈国祥

[摘 要] 数学理性思维的发展是提升数学学习能力的基础,理性思维水平体现为数学思维的灵活性、目标性、发散性和创新性等数学品质. 初中数学教学要以培养学生的理性思维、提升学生的思维品质为目标. 文章提出,通过一题多解的习题训练,比较不同的解题思路,优化解题方法,能提升学生的思维能力.
[关键词] 一题多解;解题方法;理性思维;思维品质
数学学习的基础是思维能力的培养. 学生通过学习数学概念、定理、公式等知识,来提升思维能力,培养思维品质.一题多解的试题训练,不仅能锻炼学生思维的灵活性,还能优化学生的思维品质.
本文选取了通过典型试题引导学生尝试多种解法的教学实践,与各位同行分享,供大家分析和研究.
呈现典型试题
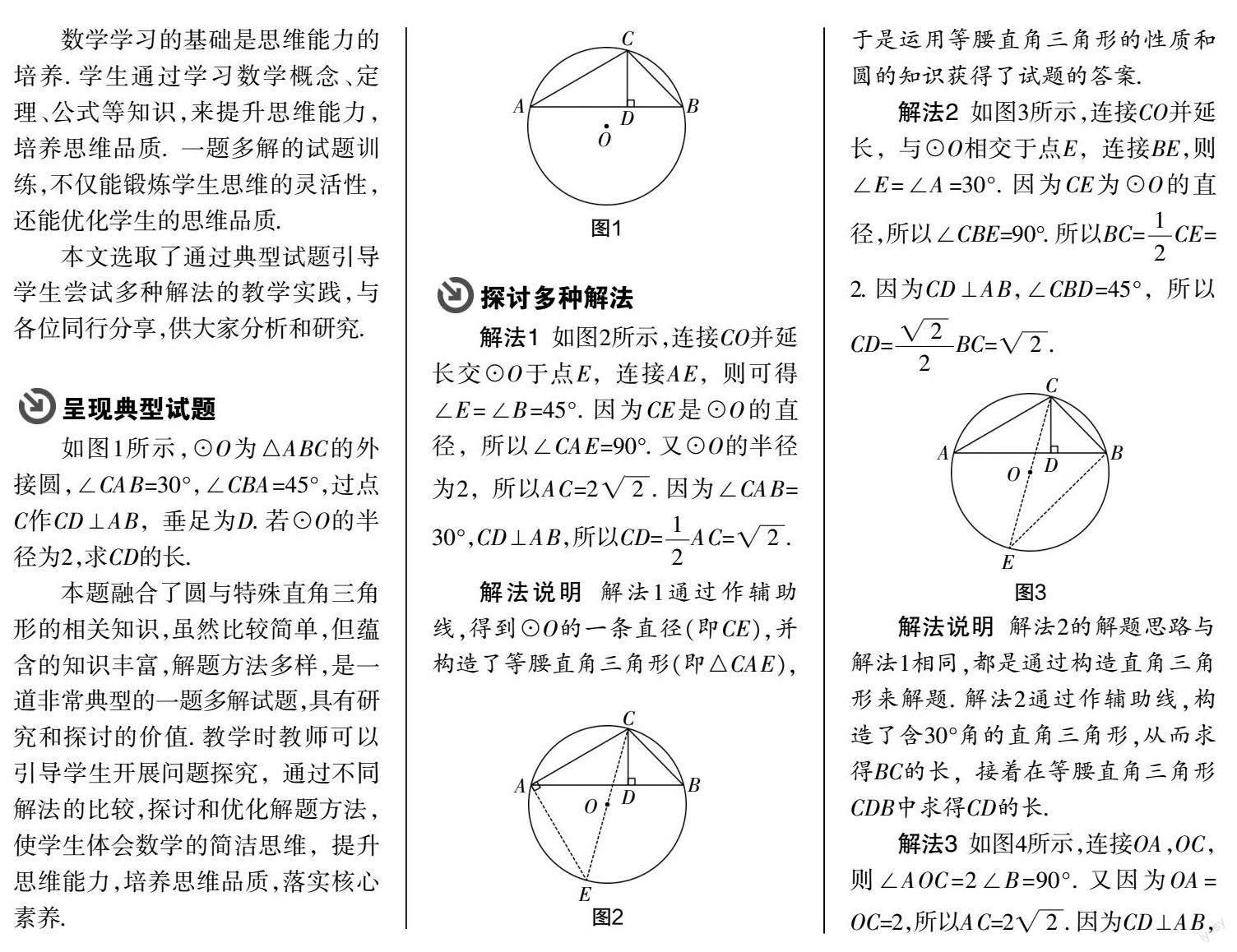
如图1所示,⊙O为△ABC的外接圆,∠CAB=30°,∠CBA=45°,过点C作CD⊥AB,垂足为D. 若⊙O的半径为2,求CD的长.
本题融合了圆与特殊直角三角形的相关知识,虽然比较简单,但蕴含的知识丰富,解题方法多样,是一道非常典型的一题多解试题,具有研究和探讨的价值. 教学时教师可以引导学生开展问题探究,通过不同解法的比较,探讨和优化解题方法,使学生体会数学的简洁思维,提升思維能力,培养思维品质,落实核心素养.
探讨多种解法
解法1 如图2所示,连接CO并延长交⊙O于点E,连接AE,则可得∠E=∠B=45°. 因为CE是⊙O的直径,所以∠CAE=90°. 又⊙O的半径为2,所以AC=2. 因为∠CAB=30°,CD⊥AB,所以CD=AC=.
解法说明 解法1通过作辅助线,得到⊙O的一条直径(即CE),并构造了等腰直角三角形(即△CAE),于是运用等腰直角三角形的性质和圆的知识获得了试题的答案.
解法2 如图3所示,连接CO并延长,与⊙O相交于点E,连接BE,则∠E=∠A=30°. 因为CE为⊙O的直径,所以∠CBE=90°. 所以BC=CE=2. 因为CD⊥AB,∠CBD=45°,所以CD=BC=.
解法说明 解法2的解题思路与解法1相同,都是通过构造直角三角形来解题. 解法2通过作辅助线,构造了含30°角的直角三角形,从而求得BC的长,接着在等腰直角三角形CDB中求得CD的长.
解法3 如图4所示,连接OA,OC,则∠AOC=2∠B=90°. 又因为OA=OC=2,所以AC=2. 因为CD⊥AB,∠CAD=30°,所以CD=AC=.
解法说明 解法3通过连接OA,OC,构造了等腰三角形AOC,并利用相同的弧所对的圆心角是圆周角的2倍,得到△AOC为等腰直角三角形,最后结合题干条件求解. 解法3同样是添加辅助线,但与解法1和解法2相比,涉及的知识点更少,因此解题步骤更简捷.
解法4 如图5所示,连接OC,OB,则∠COB=2∠A=60°. 又OC=OB,所以△OCB为等边三角形. 所以OC=BC=2. 因为CD⊥AB,∠CBD=45°,所以CD=BC=.
解法说明 解法4与解法3的思路和方法相同,但解法4利用学生最为熟悉的等边三角形知识,且直接应用了原题中的等腰直角三角形,因此解法4比解法3更加简捷.
合作探究
引导学生探究出多种解题方法并不是教学的终点,教师还要在课堂教学中引导学生将试题的不同解法进行比较与研究,指导学生在寻求最优解法的实践体验过程中实现思维的进阶,从一题多解过渡到一题优解,培养学生的创新思维.
师:请大家以小组为单位,结合表1比较这四种解法的区别和联系.
第一小组:解法1和解法2具有相同的解题思路,都是通过添加辅助线构造直径,从而形成特殊的直角三角形后求解.
第二小组:解法3和解法4的解题思路是相同的,都是连半径,形成特殊的三角形后求解.
第三小组:解法4在构造三角形时选择了等边三角形,于是可以直接利用题干中已知的圆的半径得到BC的长度为2,进而通过原题中的等腰直角三角形BDC获得答案.
师:大家分析得非常好,经过比较,我们发现解法4的解题过程最为简捷,属于最优解法.
教学启示
学习数学要对数学的本质进行探索和理解. 学会解决数学问题并不等同于解数学题,数学教学要引导学生探索数学的本源问题,培养学生的创新能力,使学生能够从知识的源头深入理解数学知识的本质,不仅知其然,更知其所以然.
1. 开展解题反思,比较不同解法
解题练习不仅要关注如何获得解题思路和答案,还要在解题后进行反思,回顾解题的过程,思考解题过程中那些烦冗复杂的部分能否变得更加简单,并尝试将较为复杂的部分变得更为简捷,试着通过直接的观察就知道整个解题过程. 在学生独立思考求解和开展多种解题方法交流的基础上,教师要引导学生回顾获取解题思路的过程,梳理解题过程中添加的辅助线,并且总结在解题过程中运用的数学基础知识和解题活动经验,从而有效地比较不同解题方法之间的本质区别. 这一过程旨在培养学生的深度思维,提升学生的思维能力.
2. 加强思维锻炼,引导探究学习
教师要引导学生开展自主探究活动,按照学生的认知水平将学生分成若干研究小组,指导学生从不同的角度围绕学习任务展开探究,并进行研究成果的交流和展示. 教师还要在学生合作探究的过程中进行指导,使学生能够有条理地对数学问题展开研究和分析,学会从不同的视角理解试题,掌握如何进行不同解法的比较,明晰不同解法之间的优劣,从而为学生开展进一步的数学学习奠定基础. 研究任务的创建为学生创设了自主学习和交流学习的平台,营造了轻松愉悦的学习环境,使学生在合作探究中培养了思维品质,提升了合作能力.
3. 开展深度学习,转变教学方式
随着课程改革的进行,数学试题不仅关注知识的考查,还关注问题的创新,它们以学生的思维品质为考查目标,突出考查学生思维的灵活性、深刻性和批判性. 因此,教师要主动改革与创新教学方式,摆脱单纯的题海战术、机械练习的教学方式,通过一题多解,引导学生开展合作学习,探讨最优解法,学会比较不同的解题方法,锻炼学生的思维,激发学生的学习积极性,使学生进行深度思考和深度学习. 本例中,教师引导学生合作探究,使他们在交流中迸发出思维的火花,出现不同的解法,并让他们在相互探讨中得到启发,发现不同解题思路之间的相同之处,从而抓住数学本质,让数学学习真正发生,使思维真正参与其中.
