胸中有丘壑，方能绘山河

刘世雄

【摘要】本文基于整体性和结构化的观念，以“二次根式”的教学为例，提出整体性教学应注重知识间的前后贯连，以旧引新；强调结构化教学应注重新旧图式体系的相互作用；整体性结构化教学应体现连贯的思想、形成普适方法，学会用相似的方法做不同的事情，感受类比中所蕴含的数学基本思想、数学基本活动经验的力量.

【关键词】初中数学；二次根式；类比

传统数学教学推崇“堂堂清”，针对每节课的知识点，推崇大容量、快节奏，以期达到当堂巩固的效果.这往往造成教学过程推进过快，知识的生成着墨不够，学生难以形成整体性的知识结构.如果教师沉迷于一个接一个的知识点教学，局限在一招一式的雕虫小技，长此以往容易迷失在局部，无法形成系统性思维，最终必将导致只见树木不见森林的后果，学生的整体性大局观的形成便成了无源之水无根之木.

《义务教育数学课程标准（2022版）》在教学建议中指出，“在教学中要重视对教学内容的整体分析，建立对未来学习有支撑意义的结构化的数学知识体系”.由此可见，新课程改革注重整体把握教学内容，倡导结构化教学.这不仅要求贯通新旧知识之间的内在关系，还要求建立联系通畅的结构化认知系统.正如章建跃博士所言：数学教学要以“研究一个数学对象的基本套路”为指导，设计出体现数学的整体性、逻辑的连贯性、思维的系统性的系列化数学活动.在类比中加强数学知识的整体架构，在类比中应用一般观念的统摄指引，以实现从“知其然”到“知其所以然”再到“何由以知其所以然”的跨越.

为说明上述基本想法，下面笔者结合近期所听到的一堂章起始课“二次根式”谈起.

1 教学过程概要与观课思考

环节一 创设情境 概念形成

问题1 教材“思考”题：

请尝试用含有根号的式子填空：

（1）2的算术平方根为____.

（2）若正方形的面积为3，则它的边长为____；

若正方形的面积为S，则它的边长为____.

（3）若矩形的面积为195，且长是宽的3倍，则它的宽为____；

若矩形的面积为S，且长是宽的3倍，那么它的宽为____.

学生思考后回答：（1） /2.（2） /3； /S.

（3） √65； √S/3.

问题 上面问题中，观察上述问题的结果.

（1）这些数与式分别表示什么意义？

（2）从形式上看都有什么共同特征？

思考归纳.

例1 当x 取何值时，下列根式有意义？

（1）√（x－2）；

（2）√（-2x+1）.

观课思考 环节一完整地展示了概念教学过程中的概念形成过程，从熟悉的面积情境出发引入课题，借助学生已有的算术平方根学习经历，既合乎知识间的逻辑连贯，又符合学生的认知结构；紧接着引导学生观察所给数与式，发现共同特征，归纳定义.

人教版初中数学教材从数到式的教学编排贯穿始终，因此开篇直接表明从数到式，体现类比的学习模式，类比分数研究分式，再次实现从一类数到一类式的跨越.故而在章起始课中，我们首先要通过类比发现研究对象.从算术平方根出发，回顾其相关知识，再通过板书算术平方根的定义来构建它与二次根式的本质联系.

环节二 互助合作 探究性质

思考 如何理解二次根式√a （a≥0）的双重非负性？为什么？

探究1 当a≥0时，“a2”化简的结果是怎样的？

观课思考 众所周知，代数性质运算中的不变性就是代数的基本性质，其基本方法是“算算看”.所以探究1和探究2均采用填空，让学生经历计算、观察、猜想、再利用不完全归纳法归纳出二次根式的性质.课堂实践中，教师引导学生自主探究，既注意培养学生观察能力，也注重提升归纳概括能力.

但是环节二性质的探究出现比较突兀，衔接不够自然，学生不仅不明白学习二次根式的性质的必要性，更谈不上理解与后续内容的逻辑关系.环节一通过类比获得了研究对象——二次根式；环节二应顺应这种类比，从已有分数到分式的学习经历，对本章学习做一个“全景式”的展望，建立起本章知识的整体架构.让学生自己可以想到将要学习的内容，让学生明白所学内容前后的逻辑关系，从而实现从“知其然”到“知其所以然”再到“何由以知其所以然”的跨越.

环节三 反思提升 实现生长

问题 谈一谈你对二次根式定义的理解.说一说这节课涉及哪些数学思想方法？

观课思考 反思提升通过“谈一谈、说一说”，回顾本节课学习的概念和性质，总结知识获得和技能形成，积累基本活动经验，感受数学思想方法.

2 教学再设计

环节一 从数到式

请尝试用含有根号的式子填空：

（1）若正方形的面积为3，则它的边长为；

若矩形的面积为195，且长是宽的3倍，则它的宽为___.

（2）若正方形的面积为S，那么它的边长为___；

若矩形的面积为S，且长是宽的3倍，则它的宽为____.

追问：（1）中表示的数√3和√65表示什么意义？

（2）中的式子与（1）中的数有怎样的关系？它们有什么共同特征？

设计意图 直接开篇明义，点明主题从数到式.例题设置再次顺应主题，结合算术平方根的定义，明白知识间的本质联系.由此因势利导得出类比要解决的第一个问题——发现研究对象，二次根式的出现水到渠成.

环节二 全景展望

问题1 事实上，式的学习的基本思路、内容和方法是一致的，你可以概括研究分式的基本思路、內容和方法吗？

问题2 类似地，你认为我们应该如何展开二次根式的研究呢？

设计意图 研究二次根式的基本思路、内容和方法与分式的研究是一致的，只需要把研究对象从分式变成二次根式.所以二次根式的学习要充分发挥分式的已有学习经验，从总结分式学习开始.为此可以采取“先行组织者”的教学策略，以问题串引导学生展开探究从而实现类比要解决的第二个问题——建立本章知识的整体架构.

问题3 我们知道分式的性质就是分式运算中的不变性规律，类似地，二次根式的性质就应该从具体的运算入手，通过算一算再发现其不变性规律.

设计意图 在整体框架下，一般观念的指引下，研究的方向清晰，研究的内容明确，在相同的研究方法指引下，不仅大大降低学习的盲目性，而且有力加强学习的主动性，学生自主发现问题和提出问题便有了可能.

环节三 回顾提升

问题4 可以概括下這节课我们是如何学习的？

设计意图 结合本节课的研究历程，引导学生形成从数到式的研究的基本套路，将内隐的思维显性化.正如章建跃博士强调的“研究对象在变，研究套路不变，思想方法不变.在整体性教学框架下，通过类比展现数学基本思想、数学基本活动经验的力量！”

3 基于整体性和结构化的数与式的教学再思考

（1）整体性结构化教学应注重知识间的前后贯连，强调以旧引新.

数学整体性教学是注重新知和旧知的前后贯连，学生的认知必须建立在已有的学习经验上，通过以旧引新促进新的认知结构的形成.

数与式经历了整数到整式，分数到分式后，二次根式是从算式思维到代数思维的又一次飞跃.二次根式与实数中算术平方根紧密联系，是非负数的算术平方根概念的进一步的抽象表示.它是特殊的含有根号的数到一般地含有根号的式.所以教学中一定要加强知识间的纵向联系，知道从哪里来？将要学习什么内容？比较中体会知识间的前后贯连，以旧引新.

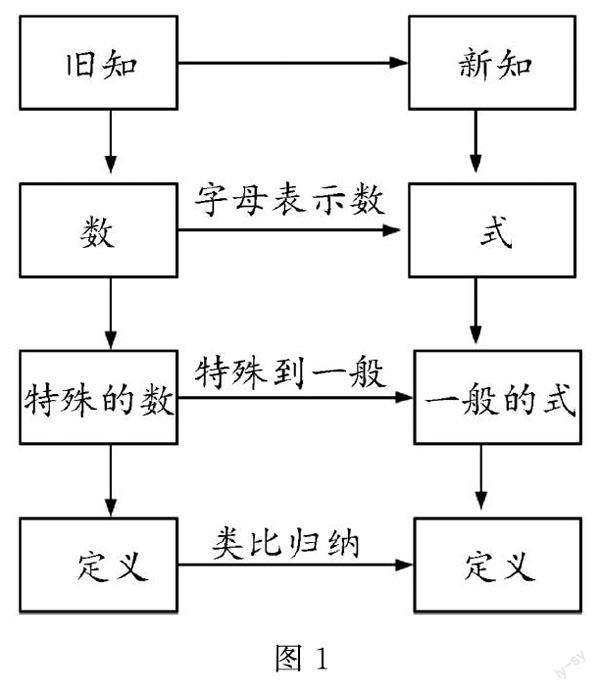
皮亚杰在《结构主义》提出结构就是图式体系的论断，认为新知学习是新、旧图式体系相互作用的过程.因此在新知的教学中，要把零碎的知识有效结成网、组成图式体系，形成知识的模块化.由此可见，在上述教学环节一中可以用图式体系（图1）回顾算术平方根的相关知识，让“旧知”可视化，图式直观化，悄无声息地将学过的知识融入新的认知结构，以旧引新.这种图式体系好似一张“联络图”，让老师有线索地教，学生有方向地学.

（2）整体性结构化教学应体现连贯的思想、形成普适方法

随着《义务教育数学课程标准（2022版）》的颁布，基于核心素养的单元教学设计成为当下新课程改革的热点，倡导以核心素养为导向做好单元教学的整体规划.由此可见，与大单元教学呼应的是整体性教学.其目的是让学生在整体的学习中，建立起适合的认知结构，形成数学学习的普适方法、基本套路.正如章建跃博士提出的代数研究的一般方法按照“引入——定义、表示、分类——性质——运算与运算律”一以贯之.正是因为研究对象相同，研究主题聚焦，研究的思路与数学思想一致，容易形成普适方法，获得基本套路.

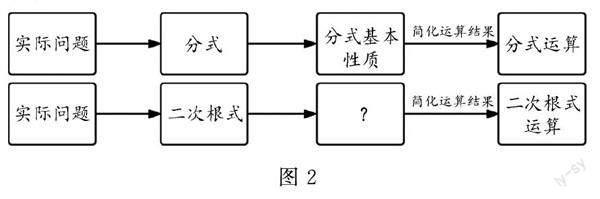
项武义教授《基础代数学》中指出“引入一种新的数（或式），就要研究它的运算……”，由于二次根式对非负实数进行开平方运算得到，因此接着的研究主题自然就是二次根式的运算，而对代数运算进行化简则是运算的本质，其化简的依据就是性质.由此可以看出，性质可以保证运算结果的简约属性.这就明白为什么会在进行二次根式运算之前要学习二次根式的性质.当然在实际教学中可以充分发挥“分式的先行组织者”的示范作用，先概括分式的研究历程、线索和基本方法，以流程图的图式体系呈现（图2），以期学生对将要学习的内容，研究的方法有一个清晰的方向.认清学习二次根式内容的大方向，厘清知识间的前后逻辑，学会用基本套路实现整体架构.

这种“全景式”的认识和把握，不仅可以明白知识的产生以及背后的逻辑；还可以将思想方法和活动经验等隐性知识转化为显性知识，让学生学会学习；这种用相似的方法做不同的事情一般方法，思想连贯、方法普适，极具迁移性.整体性结构化教学让教学主线连贯；研究对象统一，研究思想一致；整体系统规划、教学目标协同，可高瞻远瞩的教，亦能胸有成竹的学，好似胸中有丘壑，轻松绘出数学壮美的山河.

参考文献：

[1]中华人民共和国教育部制定.义务教育数学课程标准（2022年版）［M］.北京：北京师范大学出版社，2022.

[2]章建跃.章建跃数学教育随想录[M]杭州：浙江教育出版社，2017.

[3]项武义.基础代数学[M].北京：人民教育出版社，2011.

[4]刘乃志.“整体数学”教学研究与实践探索[M].北京：中国国际广播出版社，2021.

[5]邢成云.统整初中数学课程：站在课程高度教学[J].中小学课堂教学研究，2021（05）：9-12.