运用结构化教学方法发展初中生数学核心素养
2023-06-14陈静安伍海盈张然然
陈静安 伍海盈 张然然

【摘要】数学是自带结构、自成体系的一门学科,结构化教学方法是发展学生数学核心素养的有效路径.本文以“绝对值(1)”为例,阐述以教学内容为载体,运用结构化教学方法发展初中学生数学核心素养的具体做法.
【关键词】核心素养;结构化;绝对值
学生数学核心素养的发展是目前老师们关注的焦点,而数学是自带结构、自成体系的一门学科,教师充分理解数学知识结构、数学认知结构,厘清知识间的内部逻辑关系,才能更好地在教学活动中不断发展学生的数学核心素养.
1 结构化教学方法促进学生数学核心素养的发展
结构化教学方法的基础是理解数学知识结构和数学认知结构.数学知识结构是数学知识组成的一个具有内部特定规律的整体结构,概念(除原始概念外)必须定义,命题(除公理外)必须证明.数学认知结构是数学知识结构在学习者头脑里的反应,它是学习者在学习的过程中逐步积累起来的在数学方面的观念系统[1数学知识结构是客观存在的,以最概括的方式体现数学的结构化,而数学认知结构是由数学知识结构转化而来的,是学生自己加工处理后形成的结构,不同学生的数学认知结构可能存在差异.
《义务教育数学课程标准(2022年版)》明确指出:“对内容进行结构化整合,探索发展学生核心素养的路径”[2]由于教材呈现方式的限制,数学教材上的知识多是分散的.结构化教学方法就是教师从数学知识结构和学生数学认知结构出发通过问题驱动引导学生利用已有知识和数学思想方法主动参与数学探索,从中启发学生建构数学中的概念、命题等,形成结构和体系.结构化教学方法正是引导学生在一系列课堂活动中发展核心素养.
2 教学案例分析——“绝对值(1)”
2.1 教材分析
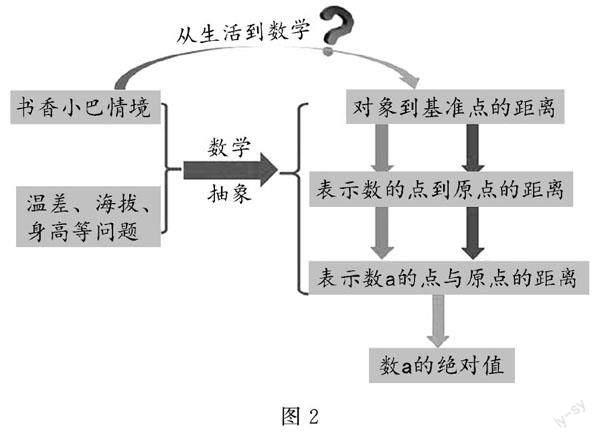
本节内容是人教版数学七年级上册第一章有理数中“绝对值”第一课时,是在小学学习了整数、分数、小数以及本章负数、有理数、数轴、相反数的基础上学习的,又是后续学习有理数加减乘除等运算以及高中的向量、复数和极限的基础.因此,绝对值不仅是有理数章节的重点、关键内容,更具有继往开来的意义与作用.(如图
绝对值课题从生活实例出发,观察点到基准点的距离,进而借助数轴,刻画一维空间里成双成对特定两点的距离,然后抽象出绝对值概念.概念的实质是定义了一种运算,并蕴含了求有理数绝对值的几何法.但因几何法中描点存在困难且效率低,故产生新的认知需求,探寻不描点的新算法.这节课内涵丰富,蕴含一个概念、两种方法、两个性质,其主要生长点是有理数、数轴和相反数.整节课蕴含的抽象能力、运算能力、推理能力的核心素养突出.
2.2 教学设计
2.2.1 溯源而上,紧扣知识生长点
设计说明 遵循奥苏泊尔“先行组织者”理论,以数轴、相反数为抓手,搭建认知的脚手架,将零散的知识点通过问题串形成结构.
教学设计
(1)同学们,还记得小学学过哪些数?结合之前学习过的负数,整数可以分为?类似的,分数呢?通过前面的学习,整数和分数合起来统称为?
(2)数在图形上怎么表示呢?数轴有哪些要素?(學生画数轴)仔细观察并思考,原点将数轴分为了几部分?数轴上可以表示哪些数?
(3)学习了数轴之后,上节课我们还学习了相反数.什么是相反数?符号不同的两数有没有相同的地方?请你在数轴上标出一组相反数,相反数有多少组?一般简洁表示为?原点是比较的?aa可以表示?-a-a可以表示?
(4)两个点不同,到原点即基准点距离却相等,能给我们带来什么启示?
核心素养 抽象能力 从相反数的概念、数轴上描相反数、再到相反数的抽象表达,在变中找不变,在个性中找共性,突出相反数的本质属性,同时强调任意数可以用字母aa或-a-a来抽象表示,为后面做铺垫.
2.2.2 生根发芽,将生活数学化
设计说明 一些生活现象存在着某种共性,当以往拥有的知识已经不足以解决问题时,就需要新知识,因此一个有趣又贴合实际的生活情境十分必要.
教学设计
(5)今年是党的百年华诞,多地开行“红色专列书香小巴”.假设两辆书香小巴从同一处O出发,分别向东、西方向行驶10km,到达红色景点A、B两处,你能用数学图形刻画出它们的行驶路线吗?
(6)两辆汽车的行驶路线相同吗?行驶路程呢?基准点是?行驶路线相反行走路程相同用数又怎么表达呢?在数轴上表示相反数的点是?它们到原点的距离为?准确描述为图中哪一个距离?
核心素养 几何直观、模型观念、抽象能力 通过动画演示及几何图形,帮助学生直观形象地理解距离与方向的关系.从小巴行驶路线抽象出图形,完成第一层次的抽象.
教学设计
(7)生活中还存在下面的一些问题.
①温差问题:假设昆明和哈尔滨昨天都是0℃,第二天昆明气温上升了6℃,哈尔滨下降了6℃,哪一个城市温差大呢?
②海拔问题:以海平面为界,玉山海拔约4000米,深海海底距离海平面2000米.哪一个距离海平面更远?
③身高问题:学校组织体检,经测量小明身高1.8m,小红身高1.5m,哪位同学更高?
核心素养 抽象能力 引入大量样本,经过作图抽象出每个问题都有一个基准点,比较时都能转化为数轴上的点到基准点的距离,揭示绝对值的本质属性,完成第二层次的抽象.
教学设计
(8)你发现这些问题有什么共同点?这种只与距离有关方向无关的数学对象称为?
(9)这里的字母aa可以用其他字母b,c等表示吗?(绝对值的符号表达动画展示)
核心素养 抽象能力 对字母aa,容易误认为aa为正数,-a-a为负数.在复习环节已经说明a可以表示的数,这里前呼后应形成结构.绝对值的符号表达是对绝对值概念的再次深入理解,通过演示动画,形象生动地解释| |.从字母aa和符号“| |”完成第三层次的抽象.概念形成不是一蹴而就的,是环环相扣、层层递进的,在此完成了三个层次的抽象.(如图REF_Ref24946\h\*MERGEFORMAT2所示)
教学设计
(10)求下列各数的绝对值.
6,-6,4.5,-4.5,3/4,-(3/4),99,0,99999,
-0.12345.
什么是|6|?求|6|,首先要?描点后数出6所对应的点到原点的距离,所以|6|=?
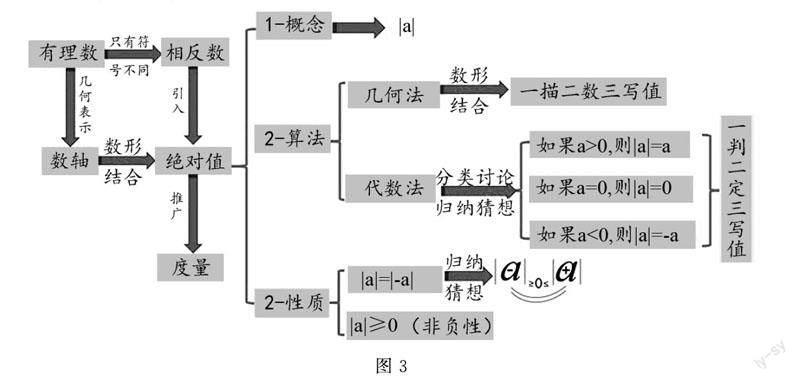
核心素养 推理能力 类比相反数的探究过程,得出几何法求值三步骤:一描二数三写值.
2.2.3 枝繁叶茂,探寻新算法
教学设计
(11)还存在|99|、|99999|、|-0.12345|这样的问题,99、99999、0.12345对应的点容易描吗?这些数用几何法求绝对值可行吗?
(12)仔细观察前面求出来的绝对值,你有什么发现?
(13)数学追求简洁美,这三个规律(即正数、负数、0的绝对值的特点)用符号语言可以怎么表示?类比几何法,你会如何命名新算法?(代数法)
核心素养 推理能力 由于描点的局限性,引導学生以成功案例为样本,提出猜想,归纳推理并验证,最后得出求绝对值的代数法.
教学设计
(14)绝对值暗藏许多宝藏,你还能发现?(|aa|=|-aa|、非负性)
核心素养 推理能力 从案例中归纳绝对值的两个性质,抽象出数学符号语言,发展推理能力.
2.2.4 明确脉络,成就参天大树
设计说明 以旧知为生长点,绝对值的概念宛如一棵大树的主干,而求值方法、性质等正如不断延伸拓展的树干,后续有理数比较大小、有理数加减、向量的模等等会形成很多分枝和叶子,绝对值蕴藏的度量思想正是这棵大树的脉络和灵魂.
教学设计
(15)小结:今天建构了哪些概念?发现了哪些运算?获得了哪些性质?研究过程中运用了哪些数学思想?(小结如图3所示)
3 结语
发展学生的核心素养是老师们共同的目标,探索发展学生核心素养的路径是每一位老师的责任.通过对“绝对值(1)”这一课题的深入剖析,我们可以看到结构化教学方法是发展学生数学核心素养的有效路径.
参考文献:
[1]何小亚.建构良好的数学认知结构的教学策略[J].数学教育学报,2002(01):24-27+85.
[2]中华人民共和国教育部.义务教育数学课程标准(2022年版)[M].北京:北京师范大学出版社,2022.
