一个二面角公式的应用与推广

湖北省武汉市常青第一中学 (430024) 叶 莉

立体几何中求解二面角问题是高考中比较重要的考查内容,主要考察学生的空间想象能力和计算能力,备受命题者的青睐.因此,掌握求二面角的一些特殊方法或公式是快速解决立体几何问题的关键.本文是从一个公式出发,通过例题解析的方式探究二面角问题的解法,以期对读者有所帮助.

图1

cosγ=cosα·cosβ②.

下面以一道例题来说明公式的应用.

例1 (2022年湖北联考题节选)如图2,在正四棱柱ABCD-A1B1C1D1中,AB=2,点E在CC1上,且CE=2EC1=2．试求二面角A-BE-A1的余弦值．

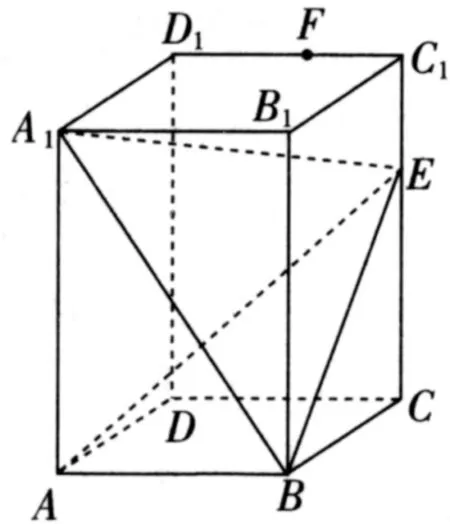
图2

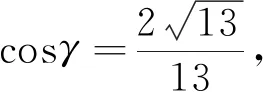
由例题1的计算过程可知,利用公式①求解,需要求3个角的三角函数值.然而有些题目中的三角函数值并不是很好求取.为此,我们需要把公式①进行一般化处理.

如图3所示,在三棱锥A-BCD中,平面ABD⊥平BCD,AB=AD,G为BD中点.设点E在棱AD上,且DE=λEA.若二面角E-BC-D的平面角θ,GA=h,GD=m,∠CBD=β,则

图3

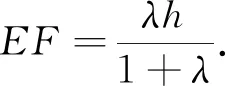
根据题意,可知二面角E-BD-C的平面角等于90°,因此由公式②可得cosα=cosβ·cosγ.

对二面角E-BC-D,应用公式①,可得

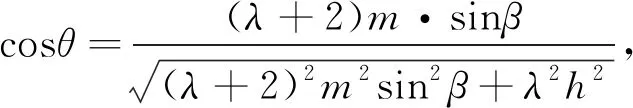
图4

(1)求证:平面OAC⊥平面ABC;

(2)若E为OC中点,求二面角E-AB-C的余弦值．

(2)由(1)知OD=1=h,DC=1=m,∠CAB=60°=β,因为E为OC中点,所以CE=EO,即λ=1.设二面角E-AB-C为θ,代入公式③得

例3 如图5,在三棱锥S-ABC中,SA=SC,D为AC的中点,SD⊥AB.

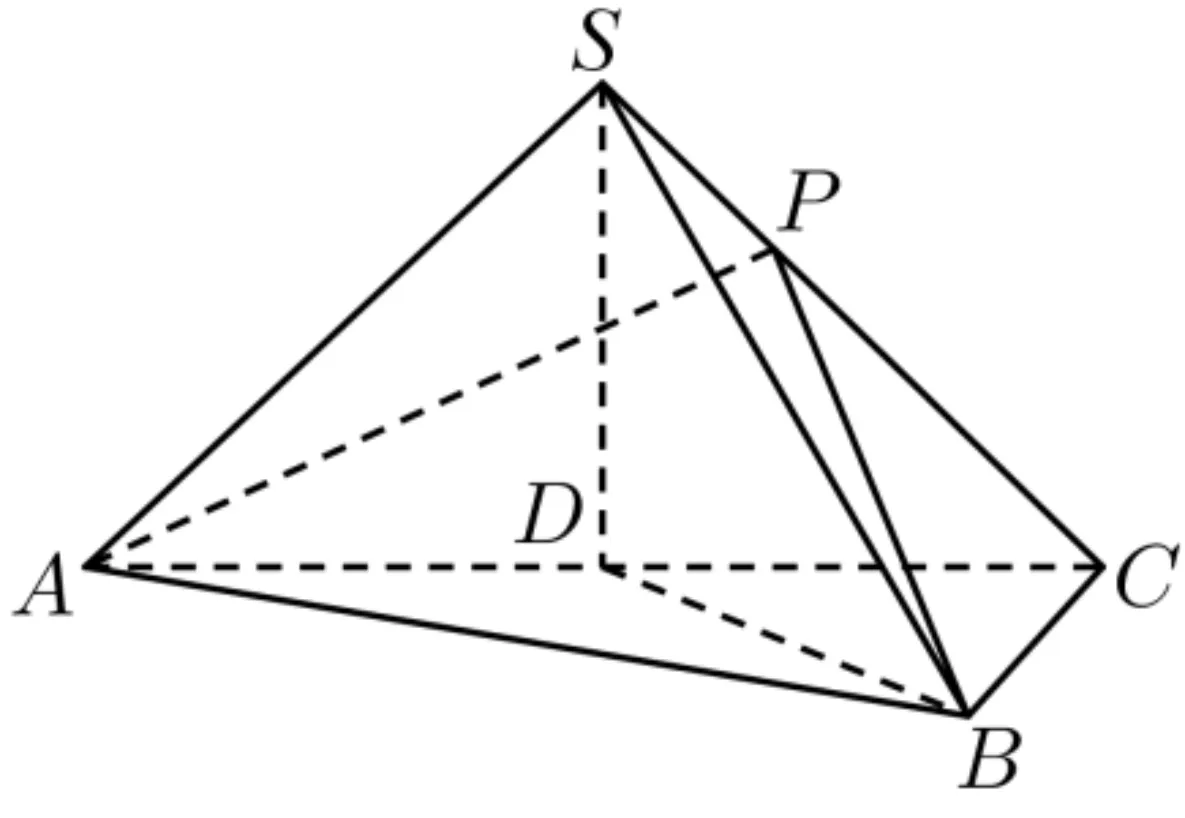
图5

(1)证明:平面SAC⊥平面ABC;

(2)若△BCD是边长为3的等边三角形,点P在棱SC上,PC=2SP,且二面角P-AB-C为30°,求VS-ABC的体积.

解:(1)因为SA=SC,D为AC的中点,所SD⊥AC, 又由于SD⊥AB,且AC∩AB=A,所以SD⊥平面ABC,又SD⊂平面SAD,从而平面SAC⊥平面ABC.