一道模考压轴题的背景与多解探析

2023-06-01山东省宁阳县复圣中学271400张志刚

中学数学研究(江西) 2023年6期

山东省宁阳县复圣中学 (271400) 张志刚

数学知识发轫于问题,活用于问题解决.剖析典型试题的命题立意、命题背景,探究多样化的解法以及沟通各种解法之间的内在联系,是发展解题水平、达到解题目的的一条值得尝试的路径,也是体味数学源头的一种方法.

一、试题呈现

(2022届南昌市高三第一次模拟测试理科第12题)已知A(-1,0),B(3,0),P是圆O:x2+y2=45上的一个动点,则sin∠APB的最大值是( ).

本题通过设置鲜活灵动的问题情境,考查一类最大张角问题,重点考查直观想象、数学建模、数学运算、逻辑推理等数学核心素养.另一方面,试题一改往常解析几何、立体几何或导数试题压轴的命题惯例,而是选取了正弦定理、圆与圆的位置关系等“基础”知识命制试题压轴,破旧立新的背后旨在引导教师破除思维定势,全面备考,科学训练,摒弃以往醉心于“押题”训练、“套路”训练的旧有思维.总之,本题立意新颖,导向鲜明,内蕴丰富,具有较高的挖掘价值.

二、命制背景

本题源于经典的米勒问题.1471年,德国数学家、天文学家米勒(Johannes,miller)向诺德尔(Chri-stian,roder)教授提出了如下有趣的问题:如图1所示,在地球表面的什么部位,一根垂直的悬杆呈现最长(即可视角最大)?上述最大视角问题因米勒首先提出,故称之为米勒问题.米勒问题广泛分布于各种实际问题中,例如探求欣赏一幅画的最佳角度、足球比赛最佳射门点等,成为世界数学史上100个著名极值问题中的首个极值问题.

将上述问题加以抽象,即为如下问题:“如图2,设M,N是角∠AOB的一边OA上的两点,试在边OB上找一点P,使∠MPN最大.”对于上述问题,我们有如下定理:

米勒定理:设M,N是角∠AOB的一边OA上的两点,点P是射线OB上异于O点的一动点,则当且仅当△MNP的外接圆与射线OB相切于点P时,∠MPN最大.[2]

证明:如图3,在射线上任取异于P点的一点P′,连接MP′,NP′,NP′与圆相交于点C.由圆周角大于圆外角得∠MCN>∠NP′M.又因为∠MCN=∠MPN,所以∠MPN>∠MP′N,得证.

图3

三、问题解答

以下分别从∠APB的正弦、余弦、正切值的最值问题探讨三个思路寻求解题突破口.

思路一:利用正弦定理和米勒定理探索最值

本题探求一角正弦值的最小值问题,联想到正弦定理,可转化为△ABP的外接圆半径最小值问题.再根据米勒定理,转化为圆与圆的内切关系问题,利用圆心距与两圆半径之间的关系式构造方程求得最小半径.

图4

思路二:应用余弦定理和基本不等式求解最值

点评:利用“1”的代换,借助基本不等式实施放缩,求得余弦值的最小值.

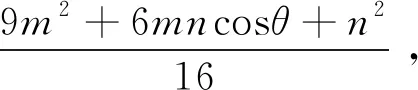
解法4:(借助斯特瓦尔特定理建立PA,PB长度间的关系式)设PA=m,PB=n,由斯特瓦尔特(Stewart)定理得PA2·OB+PB2·OA=PO2·AB+AB·AO·BO,即有3PA2+PB2=45×4+1×3×4,亦即3m2+n2=192,下同解法2.

思路三:借助两角差的正切公式和过P的直线系方程探求最值

设出点P的坐标(x,y),从∠APB的正切值切入,引入过P(x,y)点的直线系方程,然后利用原点到该直线(系)的距离小于等于圆的半径构造不等式,使问题获解.

点评:比较上述各解题思路与解法,环肥燕瘦,辩证统一.但思路1应用米勒定理,解答最为简捷明快.

四、模型应用

以米勒问题为背景的最大张角试题在历年高考中屡见不鲜,经久不衰,而米勒定理应成为解决下此类问题的首选良策.

例1 (1986年高考全国卷理科第5题)如图5,在平面直角坐标系中,在y轴正半轴(坐标原点除外)上给定两定点A,B,试在x轴正半轴(坐标原点除外)上求一点C,使∠ACB取得最大值.

图5

例2(2005年高考浙江卷理科第17题)如图6,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|:|A1F1|=2:1.

图6

(1)求椭圆的方程;

(2)若直线l1:x=m(|m|>1),P为l1上的动点,使∠F1PF2最大的点P记为Q,求点Q的坐标(用m表示).

例3(2010年高考江苏卷第17题)某兴趣小组测量电视塔AE的高度H(单位m),如图7所示,垂直放置的标杆BC高度h=4m,仰角∠ABE=α,∠ADE=β.

图7

(1)该小组已经测得一组α,β的值,tanα=1.24,tanβ=1.20,请据此算出H的值;

(2)该小组分析若干测得的数据后,发现适当调整标杆到电视塔的距离d(单位m),使α与β之差较大,可以提高测量精确度,若电视塔实际高度为125m,问d为多少时,α-β最大.

囿于篇幅,以下仅给出例3(2)的解答:

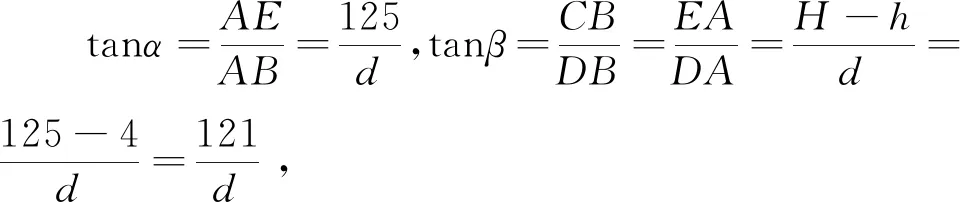
以上解法中,可以再次体会应用米勒定理大幅缩减运算量的天然优势.

值得关注的是,近年来,米勒问题在竞赛数学中也频频亮相.

例4 (2004年全国高中数学联赛第12题)在平面直角坐标系xOy中,定点M(-1,2),N(1,4),点P在x轴上移动,当∠MPN取最大值时,点P的横坐标为.(参考答案:1)

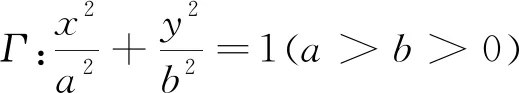
五、强化训练

1.(2022年1月广东省华附等四校联考第7题)在足球比赛中,球员在对方球门前的不同位置起脚对球门的威胁是不同的,出球点对球门的张角越大,射门的命中率就越高.如图8为室内5人制足球场示意图,设球场(矩形)长BC大约为40米,宽AB大约为20米,球门长PQ大约为4米.在某场比赛中有一位球员欲在边线BC上某点M处射门(假设球贴地直线运行),为使∠PMQ最大,则BM大约是( ).(精确到1米)