平面向量中三点共线的拓展:等和线定理
2023-06-01云南省下关第一中学郭润仙
中学数学研究(江西) 2023年6期
云南省下关第一中学 郭润仙
一、理论基础

图1
二、平面向量等和线定理
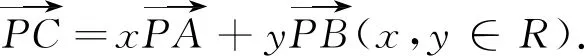

图2
(1)当直线DE经过点P时,容易得到x+y=0.
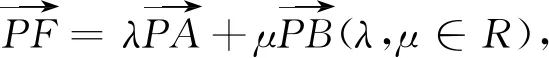

由上面的证明,我们有如下定理.

三、根据等和线求基底的系数和的最值(或取值范围)
具体求解步骤:
(1)确定值为1的等和线;
(2)平移(旋转或伸缩)该线,结合动点的可行域,分析何处取得最大值和最小值;
(3)根据长度比,巧妙计算最大值和最小值.
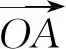

图3
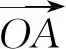
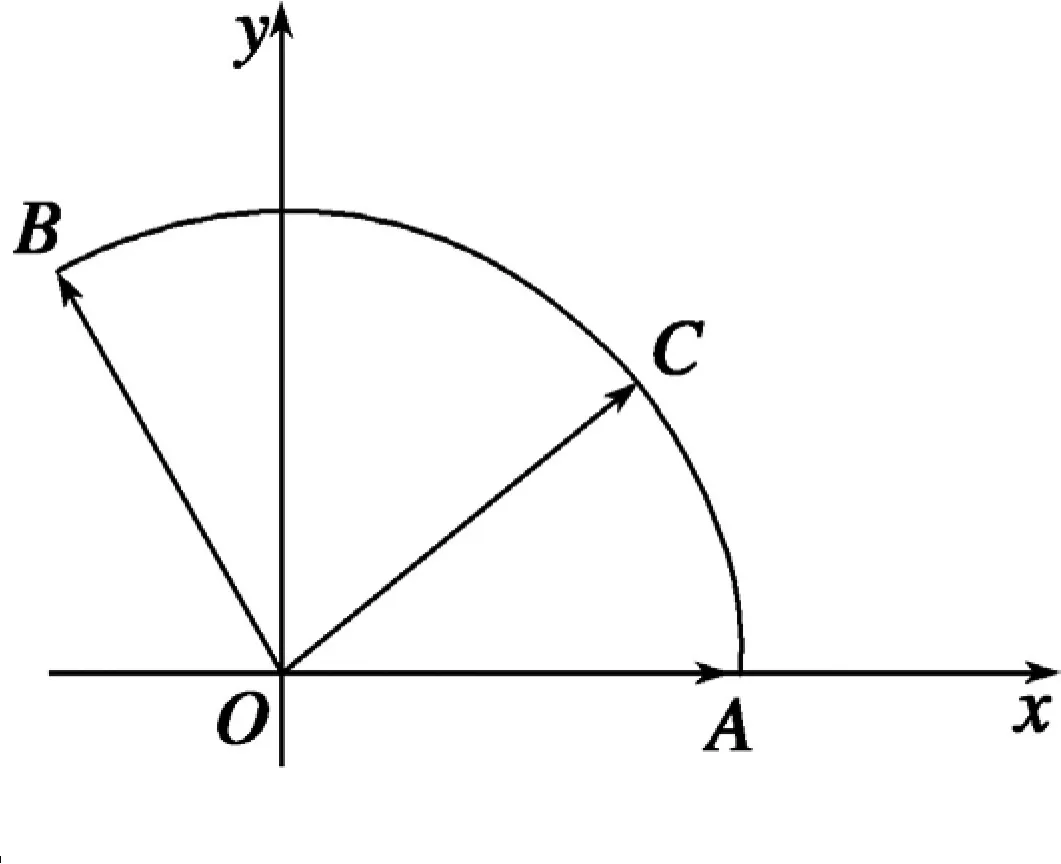
图4
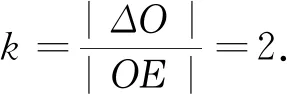

图5
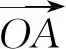

图6
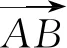
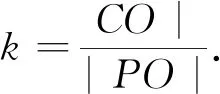

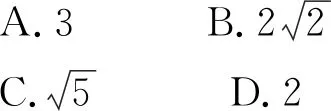
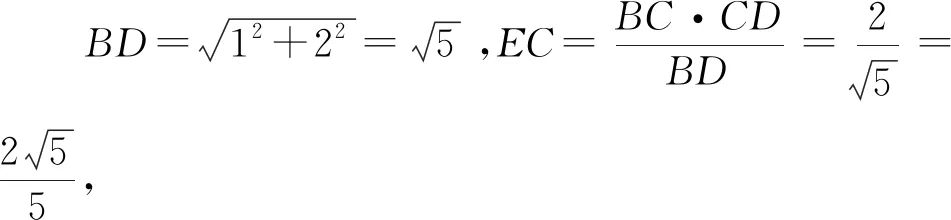

图7
设P(x0,y0),则
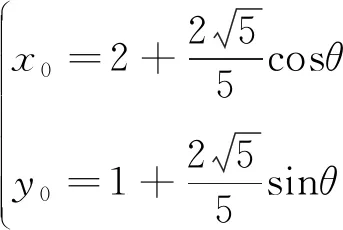


图8
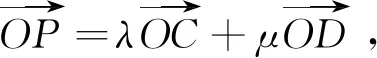

图9


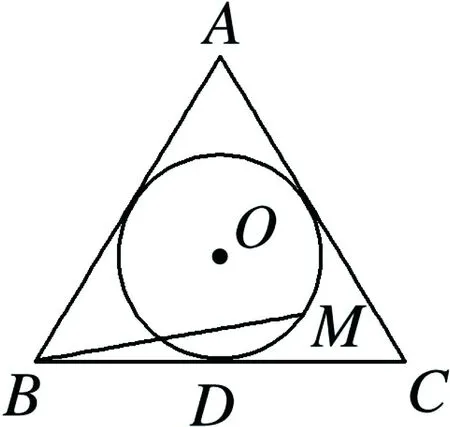
图10



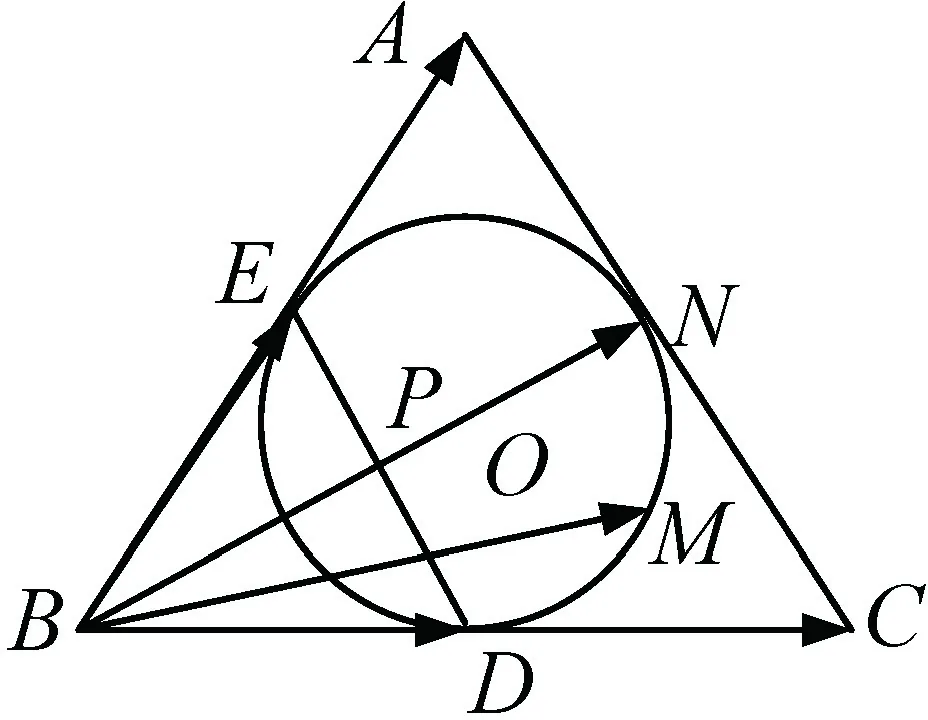
图11


图12

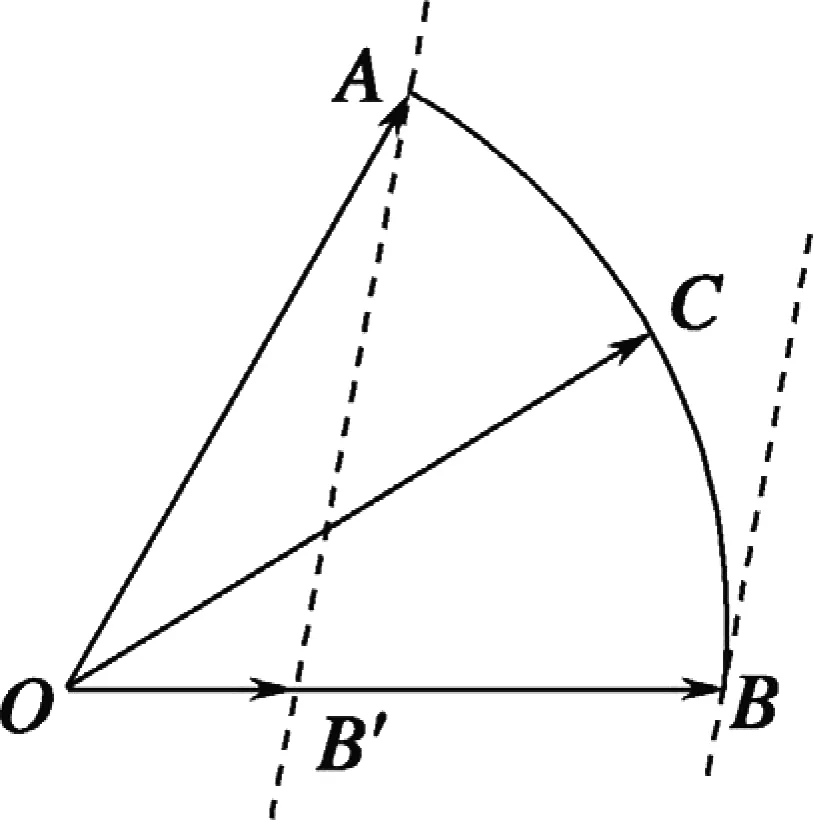
图13
综上,结合上述例1、例2、例3各自两种不同解法的对比即知:灵活运用“等和线法”处理平面向量中关于基底的系数和的最值(或取值范围)问题,往往可获得快速解法,其优点不仅体现在能够迅速找到最值情景,进而便于结合相关平面几何知识加以顺利求解,而且也体现在能够较好地培养借助“动态分析”思维,灵活求解有关最值或取值范围问题.
