带有幂次内聚断裂模型的韧性碎裂
2023-05-31徐便郑宇轩杨洪升周风华
徐便, 郑宇轩,2, 杨洪升,3, 周风华
(1.宁波大学 冲击与安全工程教育部重点实验室, 浙江 宁波 315211;2.中国工程物理研究院 流体物理研究所 冲击波物理与爆轰物理重点实验室, 四川 绵阳 621999;3.西北工业大学 航空学院, 陕西 西安 710072)
0 引言
在静态或者准静态载荷作用下,结构的破坏往往发生在某个最薄弱处,一旦发生局部破坏,从该破坏点产生的卸载使得整个结构失去承载能力。与此相对应,在动态载荷作用下,结构整体承受的加载速率大于局部破坏点对邻近区域的卸载速度,因此结构整体往往会发生多处断裂,最终断成许多碎片,即发生了碎裂。固体在突加载荷作用下的碎裂特征长期受到物理学和工程科学领域研究者的关注,能否准确预测破碎发生时间以及碎裂过程中产生的碎片尺寸,是一个重要研究课题[1-2]。Mott[3]和Mott等[4]在二战时期开展了关于材料碎裂化的研究,分析了一个处于持续塑性流动过程的理想塑性材料中,单个突发断裂位置所产生的刚性卸载阵面的传播过程。Mott认为该卸载波(Mott波)在某一个特征时间所传播距离的2倍即为碎片尺寸,但是Mott并未对该特征时间做更详细的阐述。Grady等[5-6]、Kipp等[7]认为,任何断裂过程都具有一个内禀的时间尺度,为此引入了断裂能Gc,并提出一个线性内聚断裂模型代替Mott的瞬时断裂假设,从而给出了韧性断裂发生的时间,以及在这个时间内Mott波传播的距离,这个卸载波到达距离的2倍就是碎片尺度的计算式,称为Grady-Kipp公式。
Zhang等[8-9]对高应变率下韧性金属的碎裂全过程进行实验及数值模拟,观察了膨胀圆环的整个碎裂过程。陈磊等[10]采用有限元方法,数值模拟了韧性金属圆环在快速膨胀过程中的碎裂现象,证明Grady-Kipp的线性内聚断裂模型基本适用于描述韧性碎裂,并在数值模拟中观察到断裂卸载波的激发和传播现象。郑宇轩等[11]和郑宇轩[12]对韧性金属杆在高应变率拉伸下的碎裂过程进行了数值分析,结果表明在较广泛的应变率和材料参数下,Grady-Kipp公式均可较好地给出韧性碎裂过程产生碎片的平均尺寸的下限。进一步,郑宇轩等[13]提出了最快速卸载的思想:在给定加载应变率下,受拉伸作用的材料会同时生成等间距的多个断口,存在一个最优裂纹间距,使得材料内部应力可在最短时间内卸载为零,在线性损伤演化下该间距即为Grady-Kipp公式给出的碎片平均尺寸。
韧性材料在冲击加载时的损伤演化往往是多样且复杂的。杨道明等[14]利用剖面法和金相分析对3种钢材在高应变率下的损伤演化进行了详细的研究,发现不同的损伤演化过程导致断口特征差异较大,变形过程也不一样。Levy等[15]和Doitrand等[16]从损伤起始准则与断裂耗散的能量出发,分析了裂纹拓展过程中损伤与碎片尺寸的相互联系。曹祥等[17]数值分析了不同的损伤演化路径,即内聚断裂模型的选取对断裂过程和碎片尺寸的影响,结果表明韧性材料损伤演化的非线性路径对其碎裂过程具有显著影响,非线性指标α数值越大,碎裂过程中产生的碎片尺寸越大,即偏离基于线性损伤演化路径的Grady-Kipp公式越严重。
本文从Grady分析理论假定断口的内聚力与断裂位移之间具有一种幂次非线性关系出发,理论推导出固体完全断裂所需的特征时间和断裂激发的Mott波传播距离的解析表达式,进而得到更完备的碎片尺度公式,该尺度与幂次指数k呈现弱相关特性;在0.1~1.9范围内选择不同的指数k,生成碎片的尺度将发生相应改变;进一步发现,在非线性幂次损伤路径中存在一个最快速卸载方式:当k=0.5时,损伤演化至完全断裂所需的时间最短。采用有限元Abaqus/Explicit模拟了无氧铜圆环在不同损伤演化参数下的破坏现象,数值模拟结果表明:不同k值所对应的断口形貌有明显不同,反映出断口损伤发展的韧脆性特征;采用不同k值的损伤模型,所生成的碎片平均尺度随着加载应变率和k值的变化,其特征与解析结果趋势一致。
1 Mott-Grady碎裂理论
1.1 Mott波控制碎片尺度思想
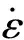
(1)
Mott利用卸载波在特征时间tMott内的传播距离作为预测应力杆碎裂后的平均尺度。在Mott理论下得到的预测碎片的平均尺度lMott公式为
(2)
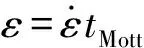
1.2 Grady线性内聚断裂模型
Grady基于理想塑性-刚性卸载分析的模型如图1(a)所示:一个处于恒应变率持续流动状态的理想塑性杆一旦产生局部断裂(区域I),将导致邻近区域发生卸载(区域II);卸载区与塑性流动区的边界称为Mott波阵面,向外侧传播;Mott波阵面未到达区域依然处于塑性流动阶段(区域III)。

图1 理想塑性材料在恒应变率拉伸过程中的断裂-卸载分析模型Fig.1 “Cohesive fracture-Mott unloading” analytical model for ideal plastic materials under tension with a constant strain rate
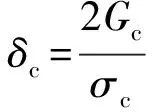
Grady-Kipp将断口张开位移δ与断口处的应力σ简化成线性关系,随着断口张开位移的增大,断口应力从初始值σc线性下降为0 MPa,如图1(b)中k=1的曲线所示,即
(3)
根据这个模型,Grady-Kipp建立了耦合I区断口应力和张开规律的动力学方程组,结合边界条件可得完全断裂所需时间为
(4)
在tGrady-kipp时刻,Mott波传播距离的2倍即可作为碎片平均尺寸的度量,因此给出如下碎片平均尺寸:
(5)
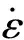
2 非线性幂次内聚力断裂模型下的碎裂过程分析
Grady在分析Mott波传播解时使用了简单的线性内聚力断裂模型,认为可能存在复杂形式的材料抵抗断裂模型[18],因此有必要对模型做扩充和改进。本文在Grady分析基础上,对内聚力损伤模型做扩展,假定断口张开位移δ与内聚力σ呈现一类影响断口延展特性的幂次非线性关系,如图1(b)所示,用下列函数描述:
(6)
式中:k大于0为幂次非线性指数,在这里视为一种材料参数:当k=1时,即为Grady的线性内聚力模型;当k<1时,材料在损伤演化过程中断口表现出的延展性较好,即碎裂后断口处断裂应变较大,断口区域材料偏韧;当k>1时,材料断口表现出的延展性较差,碎裂后断口处断裂应变较小,断口区域材料偏脆。
在断裂点损伤演化过程中的总能量耗散,即断裂能为
(7)
如式(4)、式(5)所示,材料的塑性流动应力σc和断裂能Gc将明显影响碎裂过程,是控制碎片尺度和碎裂时间的关键参数。在这两个参数相同的情况下,材料内聚力断裂曲线的具体形状,即式(6)中的幂次非线性指数k可能对碎裂过程产生影响。本文研究断裂起始后剩余拉伸应力随断口张开位移非线性递减关系对碎裂过程的影响。注意到在幂次内聚力断裂关系式(6)中,在相同断裂能Gc情况下,材料参数k、σc、δc只有两个参数可以独立变化。选择k、σc作为材料参数,则不同参数所对应的δc为
下面从刚性卸载区的运动学方程出发,推导非线性指数k对碎裂的影响:
(8)
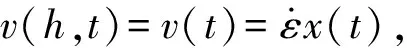
可得
(9)
式(9)给出了Mott卸载波阵面位置函数x(t)和断口张开位移δ(t)之间的关系。注意到断口的张开速度由刚性卸载区的运动所控制,即
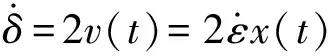
(10)
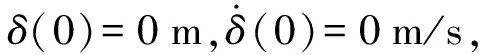
(11)
(12)
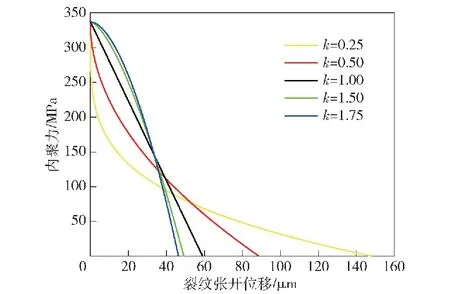
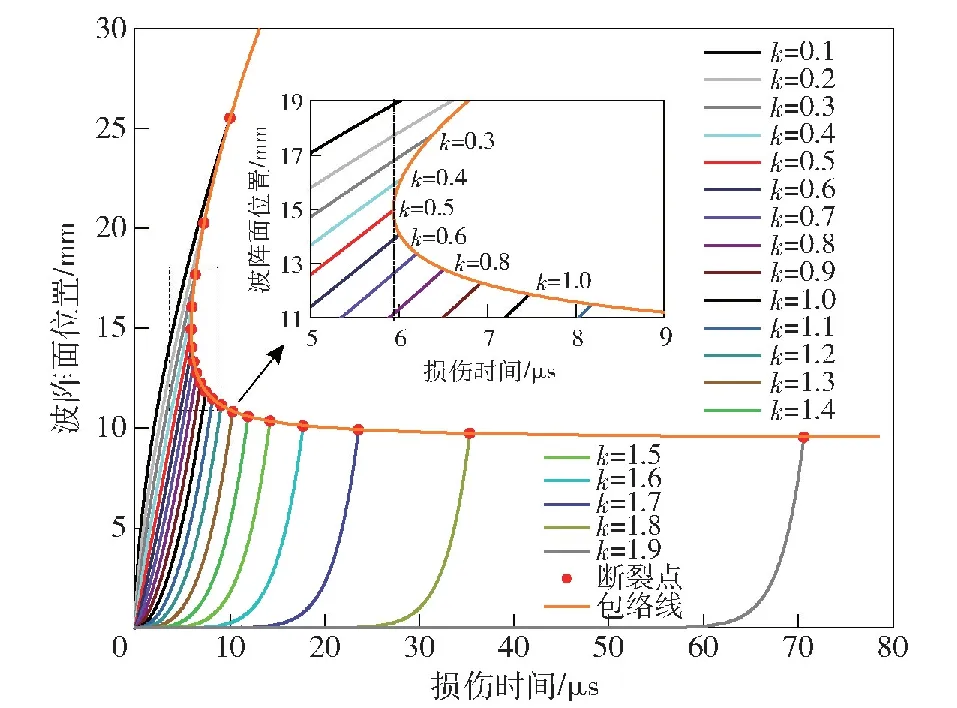
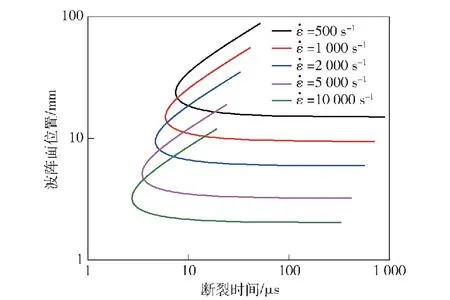
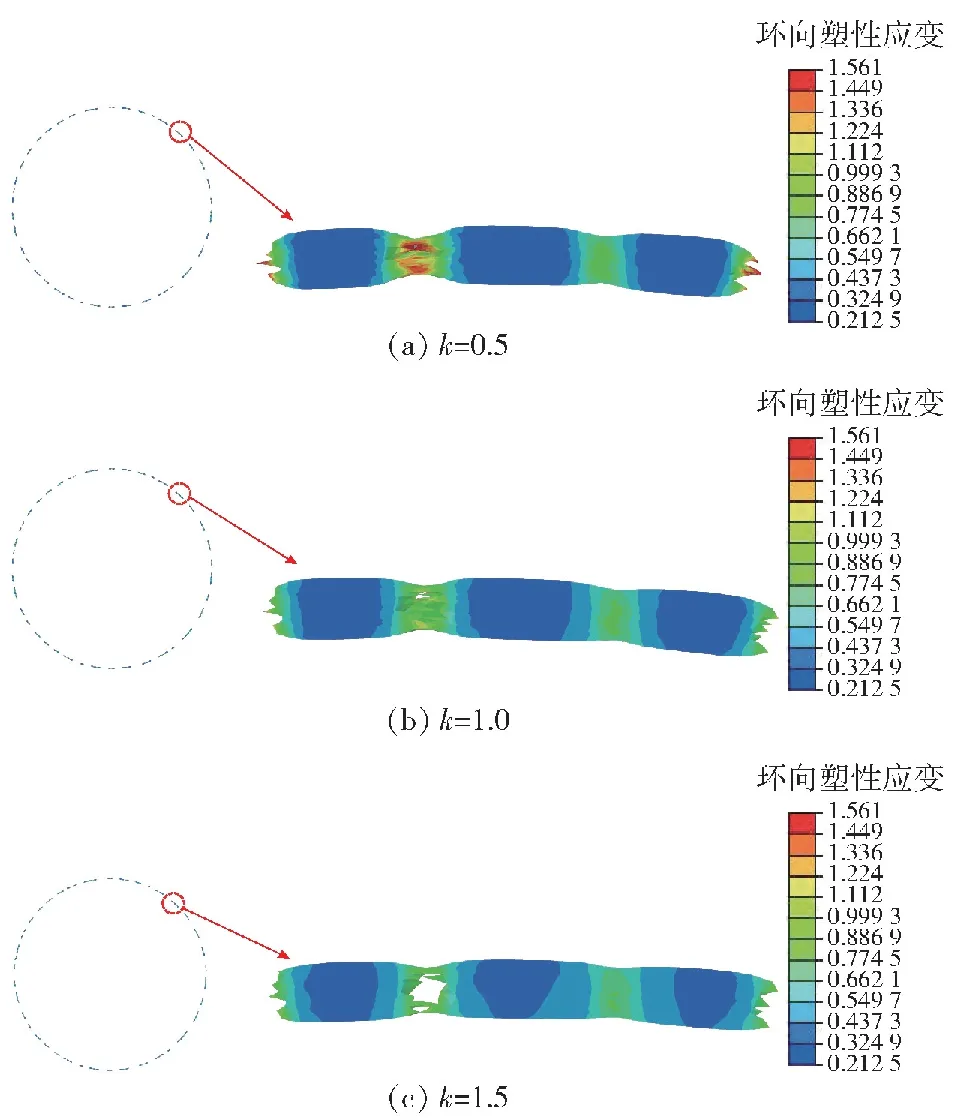
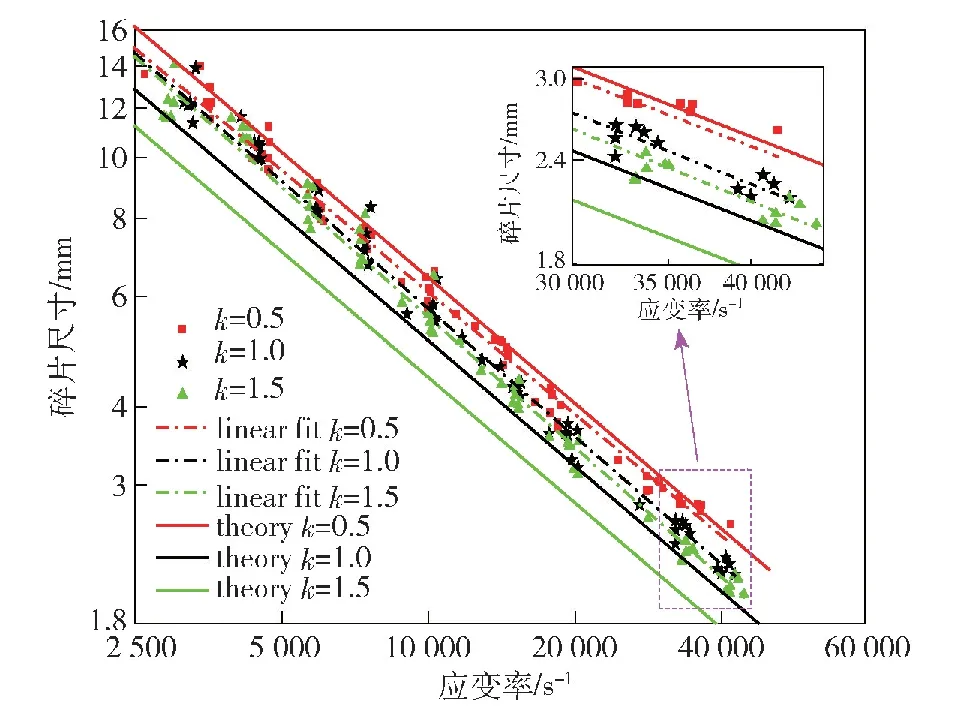
由式(12)可知当k≥2时,不能保证断口张开位移δ(t)随时间t单调递增,即此时断口无法保持自持发展状态。Grady[18]针对k=2时出现的无法自持演化现象,采用加入微小扰动,推导发现碎片尺度和断裂性质主要受后期行为影响,而受加入的扰动振幅影响不大。故而本文所设定的幂次损伤演化关系要求0 采用材料常数Gc作为控制参数,将式(7)代入式(12),得到断口开口位移δ(t)的演化关系为 (13) 将式(13)代入式(6)和式(10)中,分别可得卸载波传播距离x(t)和断口应力σ(t)演化关系: (14) (15) 裂纹发展完成时,δ(t)=δc,完全断裂时刻和卸载波传播的位置分别为 (16) (17) 由此得到幂次非线性改进的Grady碎片尺度公式为 (18) 图2 保持断裂能不变时不同k参数所确定的内聚断裂应力-断口张开位移曲线Fig.2 “Cohesive stress vs crack opening displacement”curves with different power index k with constant fracture energy 根据式(15)可绘制出断口处的内聚力随时间变化曲线,如图3所示,容易看出采用不同k值的损伤演化模型对断口卸载过程和断裂总时间产生较大影响:k取值越大,内聚力在损伤初期越难以卸载,可以想象,k取值趋于2时,断口内聚力水平将在相当长的时间内保持不变,或者下降极其缓慢;当0 图3 不同k参数下的内聚断裂应力随时间发展曲线(应变率Fig.3 Evolution curves of cohesive stress with time for 事实上,断口完全卸载的时刻tc由式(16)表征,将tc对非线性参数k求导并计算驻点,可以发现当k=0.5时tc取极(最)小值,此时断口发展至完全断裂(即内聚力卸载为0 N)所需时间最短: (19) 该数值约为线性内聚力断裂路径(k=1,Grady线性解)的卸载时间的79.4%。 由上述分析可以看出,将模型参数作为幂次非线性系数来表征材料在断口区域的韧性和脆性断裂性质,从数学上证明了k=0.5的内聚损伤演化方式对应着材料的最快速卸载,与郑宇轩等[13]提出的最快速卸载,以及Gilles等[19]基于最快速卸载思想得到的最短断裂时间一致。 进一步,由式(14)可以得到不同k参数下卸载阵面的x-t图,即Mott波的传播路径,如图4所示,这些曲线的终点,即完全断裂时刻卸载波阵面的传播位置,为式(14)所确定。在非线性指数k取一系列不同值时,每条Mott波曲线的终点可以构成一条包络线,代表断口完全断裂的时间和卸载距离。可以观察到整个“断裂时间-卸载区域”包络线在时间尺度上存在一个极小值,对应于k=0.5的Mott卸载波终点。如前所述,k=0.5时完全断裂所需要时间最短,此时Mott卸载波以恒定速度传播,即x-t为线性关系。如果k>0.5,则材料在损伤初期内部卸载过程发展缓慢,导致总断裂时间变长;如果k<0.5,则尽管早期断口张开速度变快,但由于临界张开位移δc提高,达到完全断裂的时间tc也会略有提高。总体而言,σ/σc=1-(δ/δc)0.5的损伤发展方式代表这类卸载路径中的最快速卸载路径,可能是材料损伤演化过程中的损伤断裂模型。 图4 非线性幂次指数k在0.1~1.9范围的Mott卸载波阵面随时间变化曲线,曲线终点为“断裂时间-卸载区域”包络线Fig.4 Curves of Mott wave front with time for different power index with endpoints forming an envelope of the “fracture time-unloading zone” 图5 不同k参数下的断裂时间与应变率关系Fig.5 Fracture time-strain rate relationship for different k 图6 不同应变率下的“断裂时间-卸载区域”包络线Fig.6 Envelopes of “unloading zone-fracture time” for different strain rates 为描述无氧铜圆环的材料弱化和断裂过程,采用一个包含内聚力失稳机制的损伤演化模型。该模型在有限元单元的尺度上模拟损伤破坏特性:通过单元内计算的等效塑性位移δpl(δpl等于单元几何尺寸与单元等效塑性应变的乘积)作为损伤量Da的表征, 一旦损伤开始积累,其将按照幂次关系(1-Dak)弱化材料。 表1给出了计算所用的材料本构参数。为研究幂次内聚力断裂模型对计算结果的影响,在分析过程中,保持材料的断裂能Gc及损伤开动应力σc不变,选择不同k指数模拟圆环的动态破碎过程。为精确模拟圆环的随机破碎过程,文献[10]通过网格收敛性分析得到的建议单元尺寸0.185 mm,将圆环划分成6个不同的网格,每个网格包含总数约15万个四面体2次单元,形成随机的6个数值实验样本。 表1 TU1无氧铜材料参数 选取k分别取值0.5、1.0、1.5作为典型的损伤演化代表,对一个膨胀环施加v=450 m/s的初始膨胀速度,圆环最终碎裂后的形态如图8所示,碎片最终数量分别为41个、43个、44个。数值结果显示随着k取值越大,碎片数越多,即碎片平均尺寸越小,与理论式(18)预测结果的趋势一致。在同一个应变云图标尺下,由图8中碎片局部放大的半剖面图可以观察到3种参数下碎片端面及颈缩处明显的特征差异。k值越小,断口变形区域的环向拉伸应变越大,碎片端面及颈缩处出现明显的韧性“拉丝”,并且在低应变下被断口或严重颈缩处激发的卸载波快速卸载的断口/颈缩附近区域越大。从碎片断口塑性应变可以看出,随着k取值越大,断口处的塑性应变越小,即材料断口特性偏脆,这个现象与图2的预想结果一致。 图8 k分别取值为0.5、1.0、1.5时金属环膨胀碎裂形态及碎片特征图Fig.8 Fragmentized expanding rings and typical fragments for specimens with k=0.5, 1.0, 1.5 进一步,在一个更广泛的应变率范围内(2.5×103~4×104s-1),研究不同损伤演化方式对碎片平均尺寸的影响规律。为避免网格质量及数值计算误差引起的差异,在有限元模拟中通过不同网格划分方式改变网格分布及单元总数,对6组相同应变率下的膨胀环进行重复数值实验,计算结果如图9所示,其中红、黑、绿三色实线为k分别取值0.5、1.0、1.5时理论预测的碎片尺度,红、黑、绿色的数据点为每次数值实验所得到的碎片尺寸结果,而相应颜色的虚线为对每种k值的数据点的线性拟合。从图9中可以看出以下特征: 图9 平均碎片尺度与应变率关系Fig.9 Average fragment size versus strain rate 1)在完全相同的材料参数和初始速度条件下,每组6个不同圆环的数值模拟碎片尺寸结果呈现出分散性,反映了动态碎裂的随机性特点;但是平均掉各种随机性,计算结果显示出平均碎片尺度对材料参数和应变率的依赖关系,在10%~20%误差范围内,式(18)可以较好地预测碎片平均尺度。 2)根据理论模型,k因子对平均碎片尺度lc具有影响,lc~k-1/3,k值越大、碎片尺寸越小,计算结果和理论预测的趋势一致,表现为在图9中3种颜色的实线的相对位置,与不同颜色虚线的相对位置一致;然而,实际计算结果所给出的k值对碎片尺度的影响程度远小于理论预测。 3)相比较而言,在更小的损伤演化非线性参数k(k=0.5)情况下,碎片的平均尺寸理论预测公式更接近于有限元模拟的结果,相对误差在5%~10%以内。 针对上述理论和数值模拟的结果对比,可知本文推出的碎片尺度式(18)具有较好的预测能力,在改变加载速率和非线性幂次指数k值时,数值模拟结果和理论预测值绝对数值相近,变化趋势一致。然而,理论预测的k值影响程度偏大,这是因为理论分析限定在碎裂过程的断裂-损伤阶段,即Mott波的激发和传播过程中。事实上,在一个完整的动态碎裂过程中,杆件的变形和破坏很复杂[21],包括了塑性流动、不均匀变形发展、局部失稳、损伤开动、断裂和Mott波传播等不同阶段,前期塑性失稳的复杂应力状态及有限元模型的三维几何效应等因素稀释了k值对最终碎片尺寸的影响。k值引起的碎片尺寸差异虽然没有理论那么显著,但是随着应变率增大,不同k值的影响对碎片尺寸的差异和趋势逐渐显现。 一般认为,断裂的发展所激发的Mott卸载波对碎片尺寸起着主导作用,与Grady-Kipp经典模型一样,本文的分析模型仅仅考虑上述最后一个阶段,即单个裂纹的扩展以及在此阶段向外激发的Mott卸载波所传播的距离,并以此确定碎片尺度,这与真实情况存在一定差距。本文研究结果表明,断裂路径不同,产生的碎片尺寸也有一定差别,如图4所示,k越小,则Mott卸载波传播的距离越长,卸载波对整个一维应力杆碎裂过程的影响作用越明显,这可能是卸载波控制碎片尺度的理论模型和数值模拟结果更接近的原因。 本文在Mott-Grady碎裂模型基础上,考虑损伤破坏的路径多样性,假定断口内聚力与断口张开位移之间呈一种幂次非线性关系,推导出了不同损伤模型下的断口演化过程,与临界断裂时间、Mott波传播距离,以及碎片平均尺度的解析解。经典的基于线性σ~δ关系的Grady-Kipp解作为本文解的一个特例给出。分析结果表明,保持断裂能Gc和断裂应力σc不变,代表非线性内聚力断裂路径的参数k对动态拉伸破坏过程有一定程度的影响,不同k值表征的非线性损伤演化规律控制了断裂发展过程、从而影响卸载波传播距离,具体而言:幂次指数k必须小于2,否则断口无法发生自持断裂;其次随着k的降低,Mott卸载波的传播距离单调增加,产生碎片的平均尺寸也有增加。 采用有限元方法数值模拟了韧性金属圆环在快速膨胀过程中的碎裂现象,模拟结果表明,非线性幂次指数k对韧性破碎过程的影响和理论预测结果一致,表现为:1)在广泛的应变率范围内,含非线性幂次指数k的理论推导公式能较好地给出碎片的平均尺寸随应变率变化规律;2)碎片尺寸受非线性指数k的影响趋势,有限元模拟结果与理论预测结果一致;3)非线性指数k可以用来刻画断口区域材料的相对韧性,随着指数k的降低,材料断口区域偏向韧性,能承受较大的变形。 研究还发现,在广泛的加载应变率范围内,对于幂次非线性损伤演化路径,均存在一个最快速的断口破坏路径,即非线性指数k=0.5时,损伤至完全断裂所需时间最短;k>0.5时,由于损伤前期较慢的应力卸载导致总时间更长;k<0.5时,由于完全断裂时刻的Mott波传播距离增大而导致总时间更长;k=0.5时,幂次非线性损伤发展方式对应着材料的最快速卸载路径,可能是描述材料损伤演化过程的理想损伤断裂模型。 本文揭示了一类内聚力断裂路径,即幂次函数型的σ~δ关系对动态拉伸断裂发展过程、Mott卸载波传播距离、断裂时间以及碎片尺度的影响。更复杂的σ~δ关系的影响也可以通过对本文列举的基本微分方程组进行分析或者数值计算开展分析。
3 幂次内聚力断裂路径的算例分析
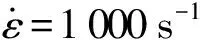

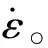

4 韧性碎裂过程的数值模拟
4.1 有限元模型和材料本构


4.2 数值模拟结果及分析
5 结论
