存在非高斯重尾分布噪声的纯方位目标跟踪算法

刘灿, 王辉, 林德福, 崔晓曦, 徐晗晖

(1.北京理工大学 宇航学院, 北京 100081; 2.中国兵器工业导航与控制技术研究所, 北京 100089;3.北京理工大学 设计与艺术学院, 北京 100081)

0 引言

纯方位目标跟踪算法是目标跟踪研究中的热点,其主要应用于无源目标定位系统。相对于有源目标定位系统,无源目标定位系统本身不向外发射电磁信号,而是获取目标的辐射源来进行跟踪定位,具有隐蔽性高、生存能力强的特点[1],在雷达被动定位、航海声呐探测、无线传感器网络等军民领域中均有着重要的应用。

纯方位目标跟踪问题的跟踪误差主要来自于模型的非线性和测量噪声的非高斯性[2],针对模型的非线性的主要挑战是纯方位角度测量和目标动力学之间的非线性关系。目前已有多种算法应用于纯方位目标跟踪中,早期的研究工作使用扩展的卡尔曼滤波器(EKF)[3],EKF采用1阶泰勒展开近似非线性量测方程和目标动力学方程,得到近似的线性测量方程和目标动力学方程。文献[4-5]通过在修正的极坐标中建立纯方位角目标跟踪问题,提高了EKF的稳定性,从而得到了修正的极坐标下的EKF(MPEKF)。除了测量方程与目标动力学的非线性影响,初始状态值的误差对于EKF的收敛也是至关重要的,较大的初始状态误差会引起发散问题[6]。此外还有更复杂的卡尔曼滤波算法应用于纯方位目标跟踪研究,如无迹卡尔曼滤波器(UKF)[7],其是一种基于确定性样点计算的滤波,不依赖于近似非线性状态和量测模型。Arasaratnam等[8]提出容积卡尔曼滤波(CKF),其基于3阶球面径向容积准则,并使用一组容积点来逼近具有附加高斯噪声的非线性系统的状态均值和协方差。文献[9]针对混合噪声提出一种应用于被动定位算法的自适应容积卡尔曼滤波(ACKF)算法。而粒子滤波器(PF)是一种基于蒙特卡洛积分的最优非线性滤波器[10],文献[11-12]将其应用于纯方位目标跟踪,但粒子滤波器的一个主要缺点是计算复杂度高,计算时间长,使得其在纯方位目标跟踪应用中的实用性有限。MILLER等[13]针对纯方位目标跟踪,用构成线性的伪线性方程代替非线性角度测量来得到线性化的递归贝叶斯估计的伪线性估计器(PLKF)。Nguyen[14]进一步发展了一种瞬时误差偏置补偿卡尔曼滤波(BC-PLEKF),通过偏置补偿测量方程的非线性,以此提高滤波器的性能。

而在非高斯噪声条件下,影响目标的跟踪精度的主要因素是测量噪声的非高斯性而不是模型的非线性[2]。在一些工程应用中,若使用不可靠传感器的异常测量值跟踪敏捷目标,系统会存在非高斯的重尾分布过程噪声和测量噪声[15-16]。在实际的应用场景中,地杂波、海杂波和偶发电磁干扰,使得雷达接收到的回波幅度突变,远高于正常值,在参数估计中形成异常值[17]。此外,目标朝向雷达的变化可能导致不规则的电磁波反射亦会在角度跟踪中产生异常值,此时测量噪声不服从高斯分布,往往呈现为重尾分布[18]。而目标飞行器的强机动以及受到的气流影响,会导致跟踪模型的状态值发生突变,诱导非高斯重尾分布系统噪声[15]。传统的卡尔曼滤波器的性能在这些具有非高斯重尾分布的系统过程和测量噪声的工程应用中会下降甚至失效。近年来,国内外提出了大量的鲁棒滤波器来解决具有重尾测量噪声的线性系统的滤波问题,如学生t分布混合滤波器[19]、异常鲁棒卡尔曼滤波器[20],以及基于学生t分布和变分贝叶斯(VB)的鲁棒卡尔曼滤波器[21-23]。然而在非高斯重尾系统过程噪声的情况下,这些鲁棒滤波器可能会失效,因为它们都假设系统过程噪声为高斯分布[19-21]。

近年来,采用变分方法来解决非高斯噪声下的非线性估计问题成为国际研究的热点。VB推断是一类近似计算复杂积分的方法,主要用于复杂的统计模型中,可以用于近似不可观测变量的后验概率估计,对于给定的模型给出观测变量的边缘似然函数的下界,然后通过相互似然的等式进行不断的迭代来获得最优解。文献[23]提出的PEKF-VB(Proximal Extended Kalman Filter-Variational Bayes)滤波器采用KL散度作为后验概率密度函数(PDF)的度量并推导出了另一种基于VB技术的非线性估计算法。文献[24]将PEKF-VB应用于星载雷达非线性目标跟踪,实现了星载雷达的跟踪精度的提高。文献[25]提出一种基于学生t分布的VB卡尔曼滤波器,将一步预测的PDF和似然PDF近似为不同自由度参数的学生t分布,用VB推断来近似重尾分布的系统过程噪声和测量噪声,提高了滤波器的估计精度。

本文基于文献[25]提出一种新的针对非高斯重尾分布噪声的鲁棒性滤波,VB修正增益卡尔曼滤波(VBMGEKF)。本文通过构造基于重尾分布的系统过程噪声和测量噪声,将一步预测的PDF和似然PDF分别建模为不同参数的带异常值的高斯分布来近似重尾分布,并将未知状态协方差矩阵的PDF模型建模为逆Wishart分布。通过引入辅助随机变量,提出一个层次高斯状态空间模型。在此基础上,通过VB推断得到近似后验PDF,以及未知状态协方差矩阵和辅助随机变量,推导出系统具有重尾分布的过程和测量噪声的线性状态空间模型后验PDF的近似闭环解析解,并结合修正增益卡尔曼滤波(MGEKF),降低纯方位目标跟踪问题中量测方程非线性的影响。仿真结果表明,该滤波器比现有的一些滤波算法具有较小的均方根误差(RMSE)。

1 问题描述

考虑一个线性离散时间状态空间模型描述的运动学系统为

xk=fk(xk-1)+wk

(1)

zk=hk(xk)+vk

(2)

式中:xk为目标k时刻的状态值;zk为k时刻的测量值;fk(xk-1)为与xk-1相关的状态预测方程;hk(xk)为系统状态与测量值相关的方程;wk和vk为系统的过程噪声和测量噪声,一般假设wk和vk均为独立的高斯分布,本文认为wk和vk为带异常值的重尾噪声。因此考虑将测量似然和一步预测建模为如下带异常值的高斯分布,即

(3)

(4)

(5)

(6)

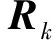
(7)

Fk-1为状态转移矩阵,Pk-1|k-1为状态协方差,Qk为系统的过程噪声协方差。当Qk为高斯分布时Σk=Pk|k-1,当Qk为重尾分布时Σk就不能等于Pk|k-1。本文使用VB来近似推断未知的矩阵Σk。对于未知矩阵Σk,需要首先选择一个共轭先验分布,因为该共轭可以保证后验分布具有相同的函数形式作为先验分布。在贝叶斯统计中,逆Wishart分布通常用作具有已知均值的高斯分布的协方差矩阵的共轭先验[25-26]。

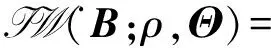
(8)

因此定义Σk为逆Wishart分布,则未知矩阵的先验分布为

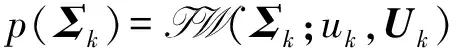
Uk=(uk-n-1)Pk|k-1

(11)

式中:n为xk维数。

同时在此处使用一种启发式算法[27],引入一个遗忘因子τ,减少前一时刻状态协方差矩阵的影响,一般取τ∈(0,1),则

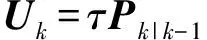
将式(12)代入式(11),可得

uk=n+τ+1

(13)

至此,一个新的基于高斯分布的状态空间模型可由式(5)、式(6)、式(11)～式(13)组成。

(14)

(15)

图1所示为层次高斯SSM。

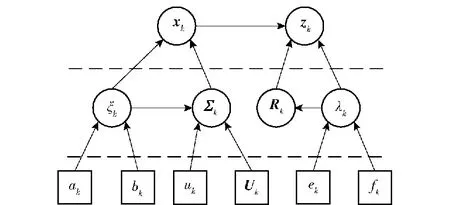
图1 层次高斯SSMFig.1 Hierarchical Gaussian State Space Model

则由式(5)～式(10)以及式(12)、式(13)构成一个基于高斯分布的层次高斯状态空间模型,从而将带有重尾分布的系统过程和测量噪声的线性状态空间模型的状态估计问题转化为基于高斯分布的层次高斯SSM的状态估计问题。

2 变分贝叶斯推断

根据贝叶斯定理,本文可以得到由式(5)～式(13)构成的层次高斯状态空间模型的联合后验分布p(Φk|z1:k,Ψk),即

(16)

式中:Φk={xk,Rk,Σk,λk,ξk},Ψk={uk,Uk,ak,bk,ek,fk}分别为模型的未知变量和先验值的参数。由于联合后验分布PDFp(Φk|z1:k,Ψk)难以求得解析解,本文采取VB方法来获取联合后验分布的次优近似解[21]。VB使用一个分布q(Φk)来近似后验分布,对数似然边际logp(z1:k|Φk)可表示为

logp(z1:k|Φk)=
F(q(Φk))+KL(q(Φk)‖p(Φ|z1:k,Ψk))

(17)

式中:F(·)为logp(z1:k|Φk)的下界函数;q(Φk)为近似后验分布;p(z1:k|Φk)为真实后验分布;KL(·)为q(Φk)和p(z1:k|Φk)之间的Kullback-liebler散度,用来衡量两个概率分布值之间的差异,KL越小,表示两个分布间的差异越小,且KL非负。

(18)

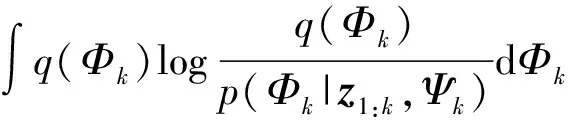
(19)

VB方法的目标是通过最小化KL来近似真实的后验值。由于KL是非负的,由式(17)可知这一目标可以通过最大化F(q(Φk))来实现。q(Φk)的最优解可由式(20)[28]得到:

logq(Δ)=EΦk(-Δ)[logp(z1:k|Φk)p(Φk|Ψk)]

(20)

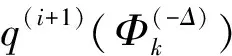
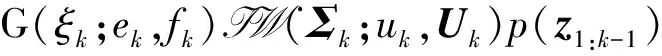
将式(21)代入式(20),得

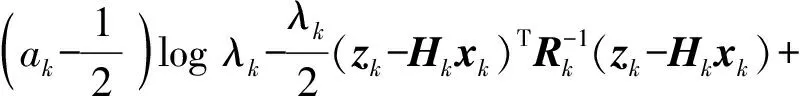
(22)

将式(22)代入式(20)并令Δ=ξk,可得

(23)

由式(23)可知q(ξk)是Gamma分布,

(24)

(25)

(26)

(27)

当选择i次迭代先验密度的参数作为下一次迭代后验密度的参数值时,可能会发生欠拟合[21],在此引入退火算法,设定退火系数κ∈[0,1],则

(28)

将式(22)代入式(20)并令Δ=Σk,可得

(29)

由式(29)可知q(Σk)为逆Wishart分布,

(30)

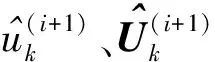
(31)

(32)

(33)

(34)

将式(22)代入式(20)并令Δ=λk,可得

(35)

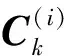
由式(35)可知q(λk)为Gamma分布,即

(36)

(37)

(38)

(39)

(40)

则

(41)

将式(22)代入式(20)并令Δ=xk,可得

(42)

此时一步预测PDFp(i+1)(xk|z1:k-1)和测量似然PDFp(i+1)(zk|xk)为

(43)

(44)

(45)

(46)

3 VBMGEKF三维纯方位目标跟踪算法

3.1 修正增益卡尔曼滤波MGEKF

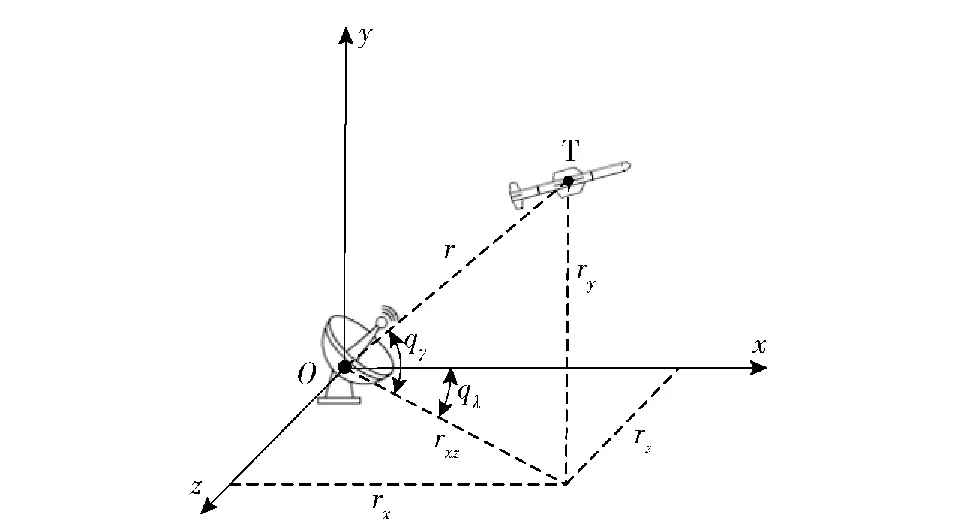
图2 三维空间目标定位示意图Fig.2 Schematic diagram of 3D spatial target positioning

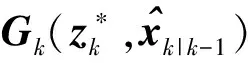
(47)

(48)

此时状态协方差矩阵为

(49)

式中:I为单位矩阵;Kk为卡尔曼增益;

(50)

式(50)中Gk的推导详见附录B,其中

(51)

(52)

(53)

(54)

(55)

(56)

(57)

3.2 VBMGEKF算法步骤

本文所提出的具有重尾分布噪声的线性状态空间模型的变分贝叶斯修正增益卡尔曼滤波器的一个步长的运算步骤如下:

步骤1输入k时刻的初始参数:k-1|k-1,Hk,ak,bk,ek,fk,Pk-1|k-1,Fk-1,zk,Qk,Rk,n,τ,L,κ。

步骤2预测步骤

k|k-1=Fk-1k-1|k-1

(58)

设定跟踪模型为匀速运动模型,T为步长,I3为维度为3的单位矩阵。

(59)

(60)

步骤3变分贝叶斯近似更新

fori=1:L

1)初始化:

uk=n+τ+1,Uk=τPk|k-1,k|k=k|k-1,Pk|k=Pk|k-1

2)VB迭代

代入式(24)更新q(i+1)(ξk);

代入式(30)更新q(i+1)(Σk);

代入式(36)更新q(i+1)(λk);

end

3)修正增益卡尔曼滤波MGEKF

(61)

(62)

(63)

(64)

(65)

4 仿真分析

对本文提出的VBMGEKF算法针对纯方位目标跟踪问题进行仿真验证,仿真模拟单站固定无源系统对机动目标的定位跟踪,以验证算法的跟踪性能和鲁棒性;另外将本文提出的VBMGEKF算法与EKF、UKF、PEKF-VB、VBEKF进行比较。

4.1 重尾噪声建模

构建重尾过程噪声wk与测量噪声vk,按照文献[30]设定过程噪声协方差Qk和测量噪声协方差矩阵Rk为缓慢时变矩阵,分别为

(66)

(67)

式中:N为仿真时间,此处设置为150 s;Δt=T;I2为维度为2的单位矩阵;q和g用于调节时变噪声协方差Qk和Rk的大小,此处设置q=1,g=100。

设定非高斯重尾分布的系统过程噪声以及测量噪声为

(68)

式中:a为异常值大小的调节参数;w.p表示取该项分布的概率。

状态值为xk=[rxkrvkrzkvxkvvkvzk]T,设定x0=[4 000 2 000 10 500 650 150 1]T为初始状态值,P=diag[1 0002500250025025021]为初始状态协方差。为比较现有滤波器和本文提出的滤波器的性能,选择位置和速度误差的均方根为性能标准,其定义如下:

(69)

(70)

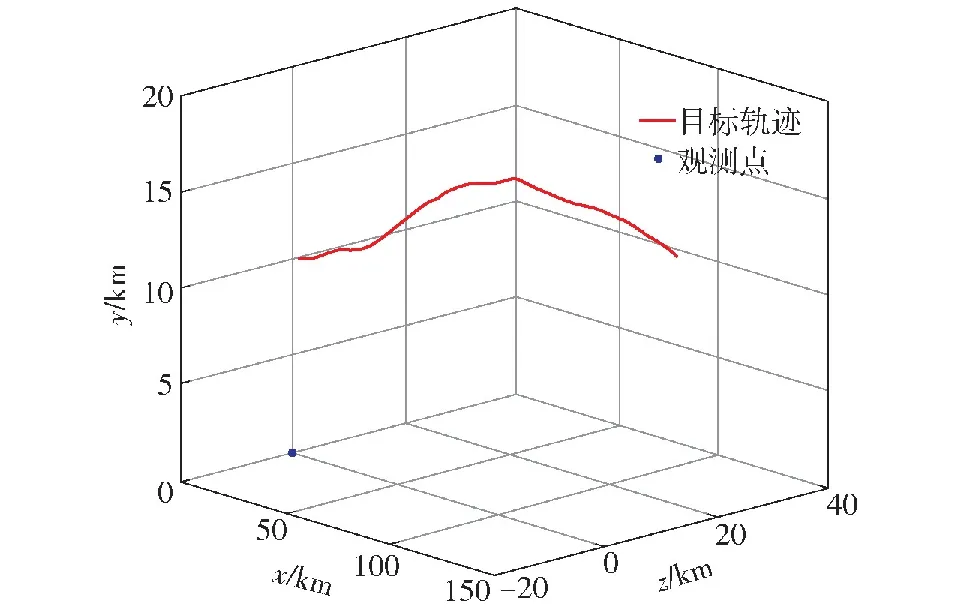
图3 跟踪目标轨迹场景示意图Fig.3 Diagram of target tracking trajectory scene

4.2 仿真校验

4.2.1a为固定值

分别取a=300、a=500和a=700,此时系统的过程噪声wk以及测量噪声vk均为带异常值的非高斯重尾分布噪声。仿真结果如图4～图15及表1所示。本文的算法参数设置为τ=10-5,L=4,ak=5,bk=5,ek=5,fk=5。其中图4、图8、图12为目标跟踪距离误差图,图5、图9、图13为相对跟踪误差,即目标跟踪误差与实际距离的比值,图6、图10、图14为跟踪目标x轴方向的速度误差图,图7、图11、图15为跟踪目标x轴方向的加速度误差图,表1为不同噪声下的各算法的目标跟踪距离误差的RMSE。

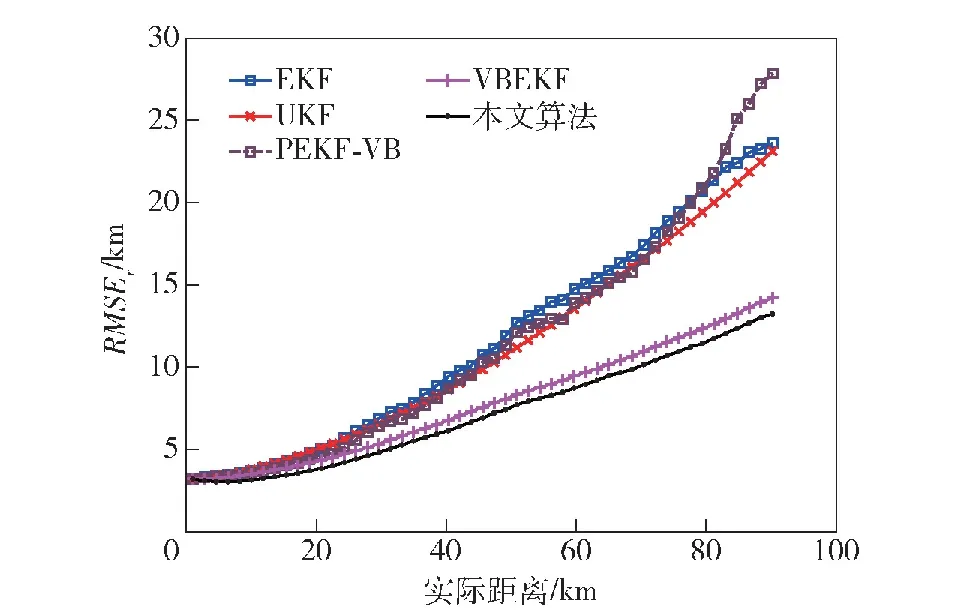
图4 目标跟踪距离误差RMSE(a=300)Fig.4 RMSE in distance error of target tracking (a=300)

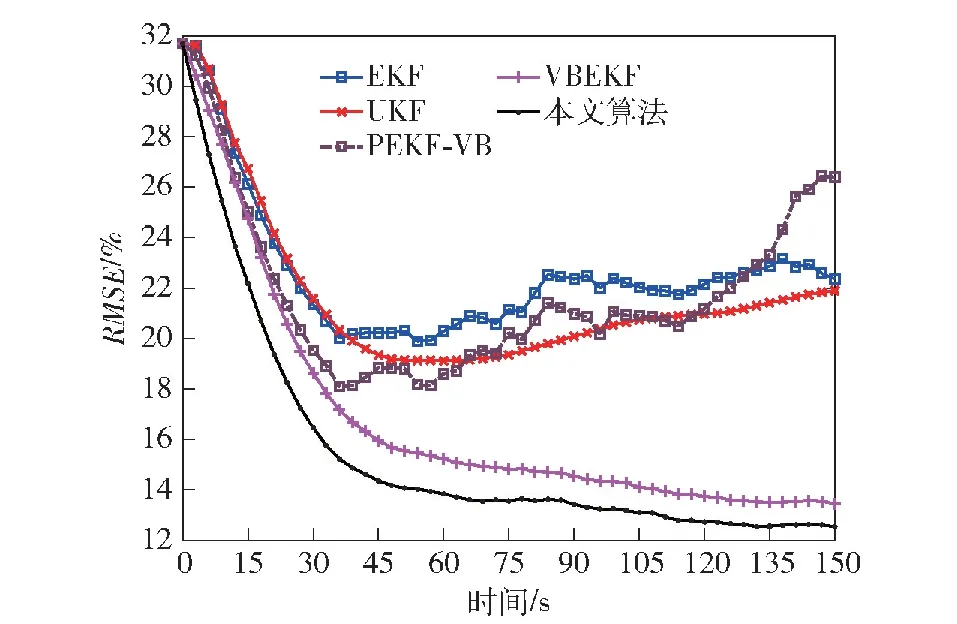
图5 目标跟踪相对误差RMSE (a=300)Fig.5 RMSE inrelative distance error of target tracking (a=300)

图6 目标跟踪速度误差RMSE(a=300)Fig.6 RMSE in velocity error of target tracking (a=300)

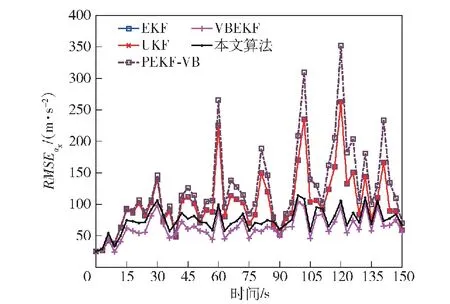
图7 目标跟踪加速度误差RMSE (a=300)Fig.7 RMSE in acceleration error of target tracking (a=300)

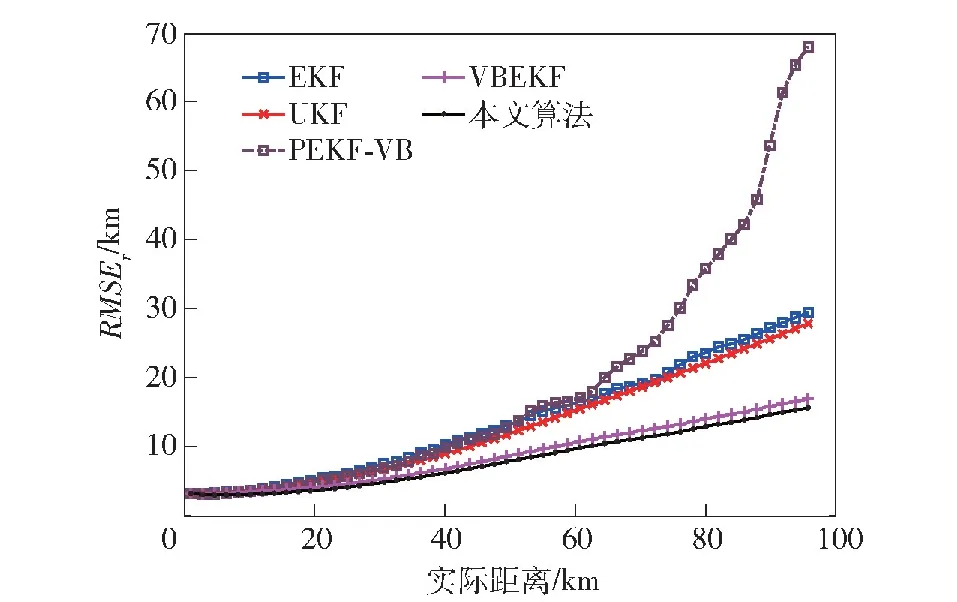
图8 目标跟踪距离误差RMSE(a=500)Fig.8 RMSE in distance error of target tracking (a=500)

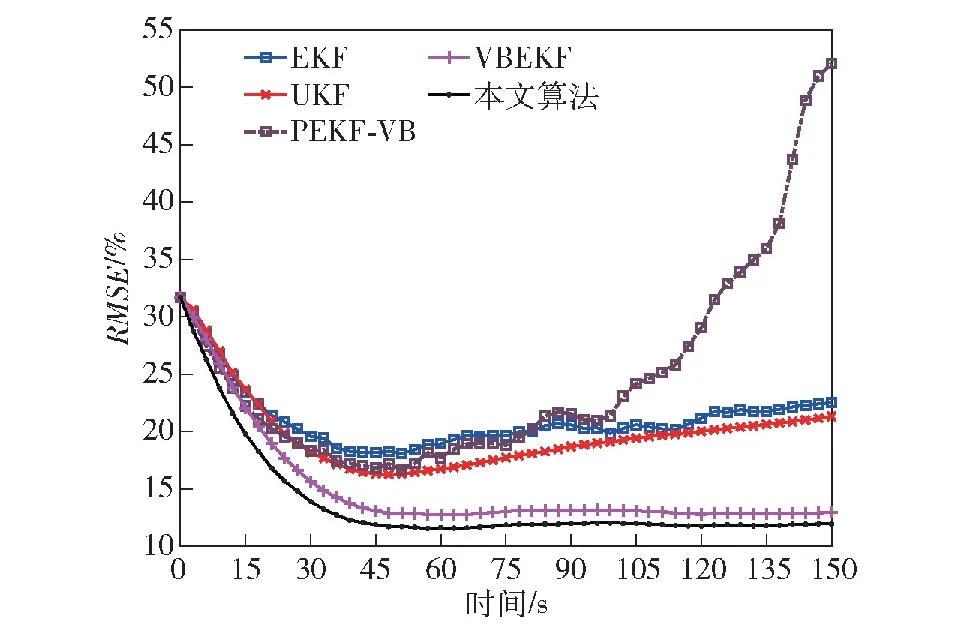
图9 目标跟踪相对误差RMSE (a=500)Fig.9 RMSE in distance relative error of target tracking (a=500)

图10 目标跟踪速度误差RMSE(a=500)Fig.10 RMSE in velocity error of target tracking (a=500)

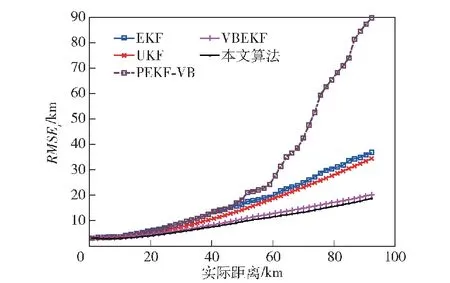
图12 目标跟踪距离误差RMSE(a=700)Fig.12 RMSE in distance error of target tracking (a=700)

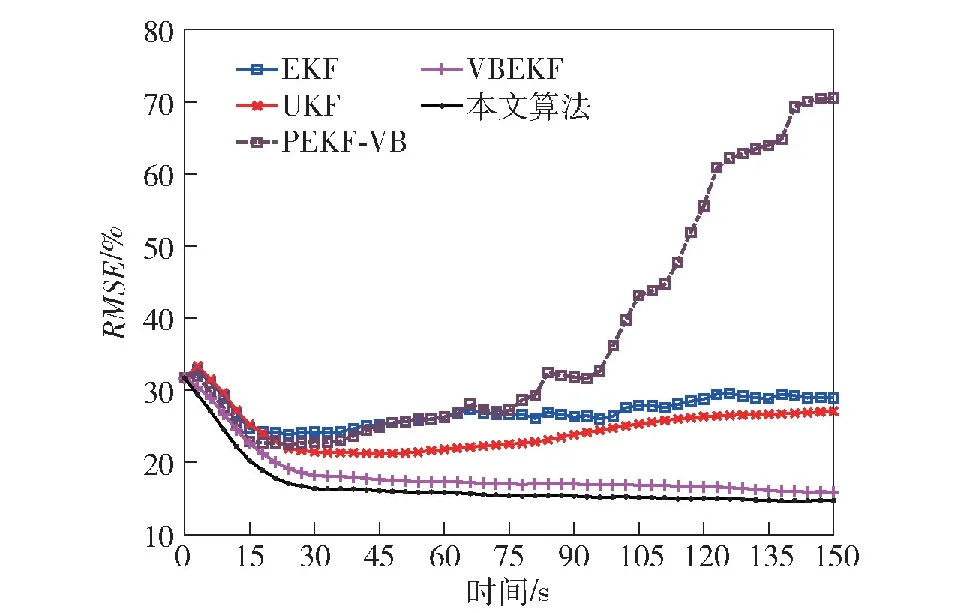
图13 目标跟踪相对误差RMSE (a=700)Fig.13 RMSE in relative distance error of target tracking (a=700)

图14 目标跟踪速度误差RMSE(a=700)Fig.14 RMSE in velocity error of target tracking (a=700)

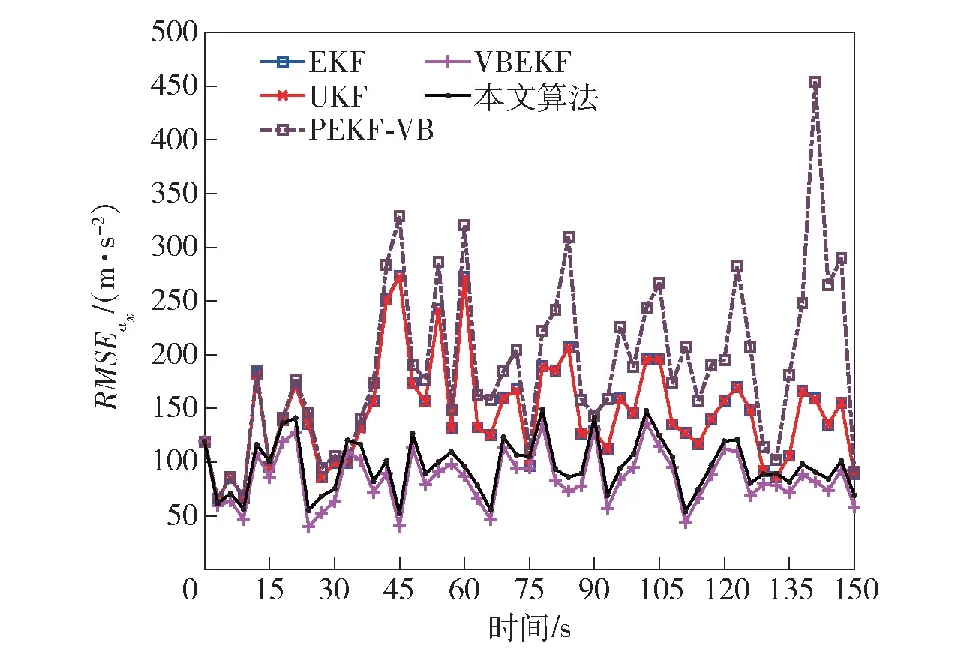
图15 目标跟踪加速度误差RMSE(a=700)Fig.15 RMSE in acceleration error of target tracking (a=700)

表1 不同噪声分布下的平均RMSE

从图4、图8、图12中均可以看到,所有算法的跟踪误差都随着时间增大,这是因为目标实际运动轨迹为由近到远,被测角的角速度减小,目标仍然维持高机动,跟踪难度上升,因此如图4、图8、图12所示,所有滤波算法的跟踪距离误差的变化趋势均为由小变大,其中本文算法的RMSE相对于其余算法最低。观察目标跟踪相对误差RMSE,各个算法在异常值处于不同水平时的趋势相同,以图5为例,可以看到,在40 s之前所有算法的相对误差均呈现下降趋势,但是由于EKF算法与PEKF-VB算法将噪声的先验分布建模为高斯分布,其在非高斯重尾噪声下滤波器性能下降严重,两个算法均在40 s后逐渐发散,且在105 s后PEKF-VB算法发散更严重;UKF算法由于采用确定性样点来逼近状态的后验

概率密度,具有一定的鲁棒性,因此具有比EKF算法、PEKF-VB算法更好的跟踪性能,但是仍然在40 s之后发散,但相对误差相对于EKF算法与PEKF-VB算法更低;本文所提的VBMGEKF算法与文献[25]提出的VBEKF算法,将系统过程噪声与测量噪声均建模为重尾噪声,本文算法在35 s处逐渐收敛到15%,平均较VBEKF算法低2%左右,可以看出本文的算法性能更佳。另外从图6、图10、图14及其局部放大图中可以看到,本文算法在一开始对目标速度的估计相对于其他算法就具有更小的误差。在图7、图11、图15所示的加速度误差图中,可以看到本文所提算法与VBEKF算法对加速度的估计相对于其余算法具有更好的效果。

从表1中可以看出,本文算法与VBEKF均具有较小的RMSE,在a=500、a=300和a=700时,即存在不同程度异常值的重尾分布噪声下具有较好性能,这是因为本文算法与VBEKF算法均将一步预测的PDF和似然PDF建模为重尾分布,通过VB推断得到状态协方差与测量噪声的后验分布信息,因此比其他算法有更佳的性能,但同时本文还结合MGEKF,降低量测方程非线性的影响,因此如图4～图15所示,本文算法相比其他算法在跟踪距离误差、相对跟踪误差、目标速度误差、加速度误差中均具有较小的RMSE。

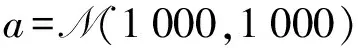
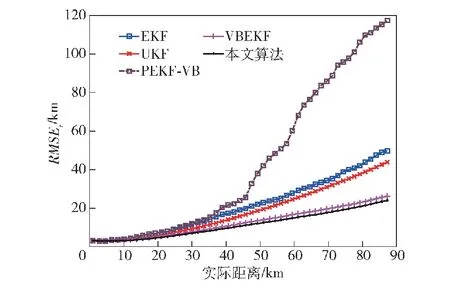
图16 目标跟踪距离误差RMSE Fig.16 RMSE in distance error of target tracking

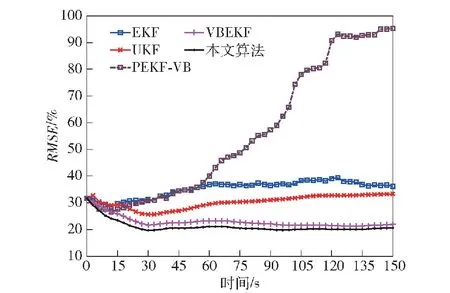
图17 目标跟踪相对误差RMSEFig.17 RMSE in relative distance error of target tracking

图18 目标跟踪速度误差RMSEFig.18 RMSE in velocity error of target tracking

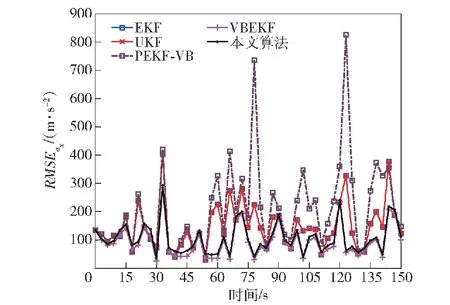
图19 目标跟踪加速度误差RMSEFig.19 RMSE in acceleration error of target tracking

7 结论

1)本文针对纯方位目标跟踪中存在的非高斯重尾分布噪声问题提出了一种新的基于高斯分布的变分贝叶斯自适应鲁棒滤波算法VBMGEKF,通过构造基于高斯分布的层次高斯模型来拟合重尾分布的系统过程噪声与测量噪声,使用变分贝叶斯近似,迭代得到模型的未知变量和先验值的参数,推断出系统状态协方差与测量噪声协方差,并且针对纯方位目标跟踪的观测方程采用MGEKF,降低观测方程非线性带来的误差。

2)经过数值仿真,本文验证了在纯方位目标跟踪问题中VBMGEKF相对其他非线性滤波EKF、UKF、PEKF-VB、VBEKF在两种重尾分布噪声下均具有更高的跟踪精度与鲁棒性。

3)在后续的研究工作中,将深入探索本文算法在无源多站协同探测中的应用,进一步提高目标跟踪精度。