126 kV三断口串联真空断路器电容和断口分压的量化研究
2022-04-29马云龙刘威峰周秀田天白金罗艳
马云龙,刘威峰,周秀,田天,白金,罗艳
(国网宁夏电力有限公司电力科学研究院,宁夏银川 750011)
0 引言
由于日益严格的环境保护要求,目前在高压断路器领域占据主导地位的SF6断路器将受到极大的限制。发展环保型的高压真空断路器被认为是限制SF6排放量的有效途径之一[1]。发展更高电压等级的真空开关主要有发展高电压等级单断口真空断路器和发展多断口真空断路器这两个途径[2]。由于真空间隙介质的饱和特性,单断口断路器的开断性能受到了极大的限制,目前挂网运行的仅有西安交通大学研制的126 kV 单断口真空断路器[2-3],因此应用于高电压等级的多断口真空断路器成为了重要的研究方向[4-5]。对于高电压等级的多断口真空断路器,由于杂散电容的存在,其断口电压分布并不均匀,不均匀程度与多断口的布置方式密切相关。文献[6]对多断口真空断路器绝缘击穿统计特性的研究表明,各断口的电压分布规律实质上决定了多断口真空断路器的击穿电压增益倍数,在静态条件下,其电压分布主要由间隙电容和杂散电容参数决定。文献[7]进行了双断口真空断路器开断能力试验,试验结果表明,即使2个断口的燃弧特性基本一致,暂态恢复电压的分布在其峰值时刻亦较弧后初期明显不均匀,这亦是由双断口结构的分布电容参数决定的。大连理工大学首先提出了采用光控模块式真空断路器单元组成多断口真空断路器的概念[8-9]。文献[10]对光控模块式真空断路器的概念进行了进一步的分析。文献[11]进行了不同均压电容参数下的双断口真空断路器开断能力试验,结果表明,均压电容可改善双断口结构的电压分布,但若电容值过大,其改善作用会趋于饱和甚至降低,特别是在断口间燃弧特性不一致时;因此,得到多断口真空断路器的分布电容参数对选择合适的布置方式和均压措施具有重要意义。
本文提出一种V型串联排布的三断口真空断路器,建立计算模型,利用表面电荷法计算出断路器的分布电容,分析电容类型对断口分压的影响,夹角的变化对分布电容值变化的影响以及对断口分压产生的影响,结果可为多断口真空断路器的断口均压和排列方式结构优化提供一定指导依据。
1 多断口真空断路器模型的建立
模型采用三个灭弧室呈V 型串联而成,相邻两个灭弧室之间的夹角为θ,串联真空灭弧室距离地面距离为1 000 mm。真空灭弧室采用40.5 kV的商用瓷壳灭弧室。额定开距下,断口分布电容最小,电压不均匀分布程度最大,因此采用20 mm的额定开距作为电压分布计算模型的结构参数,求解域为该模型的20倍。模型如图1所示。
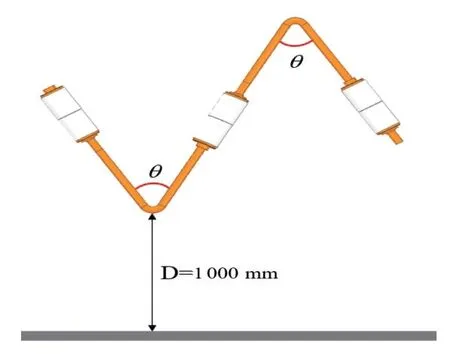
图1 126 kV 三断口真空断路器有限元模型
考虑到真空灭弧室和断路器的内部结构较复杂,因此对三断口真空断路器做一定简化,仅考虑动静触头、动静导电杆、主屏蔽罩和真空灭弧室的连接母线。空气区域的外表面和大地设置为接地边界条件,左端导体和第一个断口的静触头设置为高电位,右边末端断口的导体和静触头设置为零电位。
2 电压分布和分布电容的分类计算
2.1 电压分布特性
母线夹角θ取60°,为了研究每个断口承担的电压比例,在导体1 处施加激励为126 kV,在导体4 和导体5 施加地电位,悬浮罩等其他导体为悬浮电位。
图2(a)为仿真得到的三断口电压分布云图,断口间的电压分布极不均匀,为了描述断口分压的不均压程度,引入了不均匀系数n。不均匀系数n定义为断口两端实际的电压与断口电压分布均匀时的断口电压之比,一般不均压系数要求为0.9~1.1。
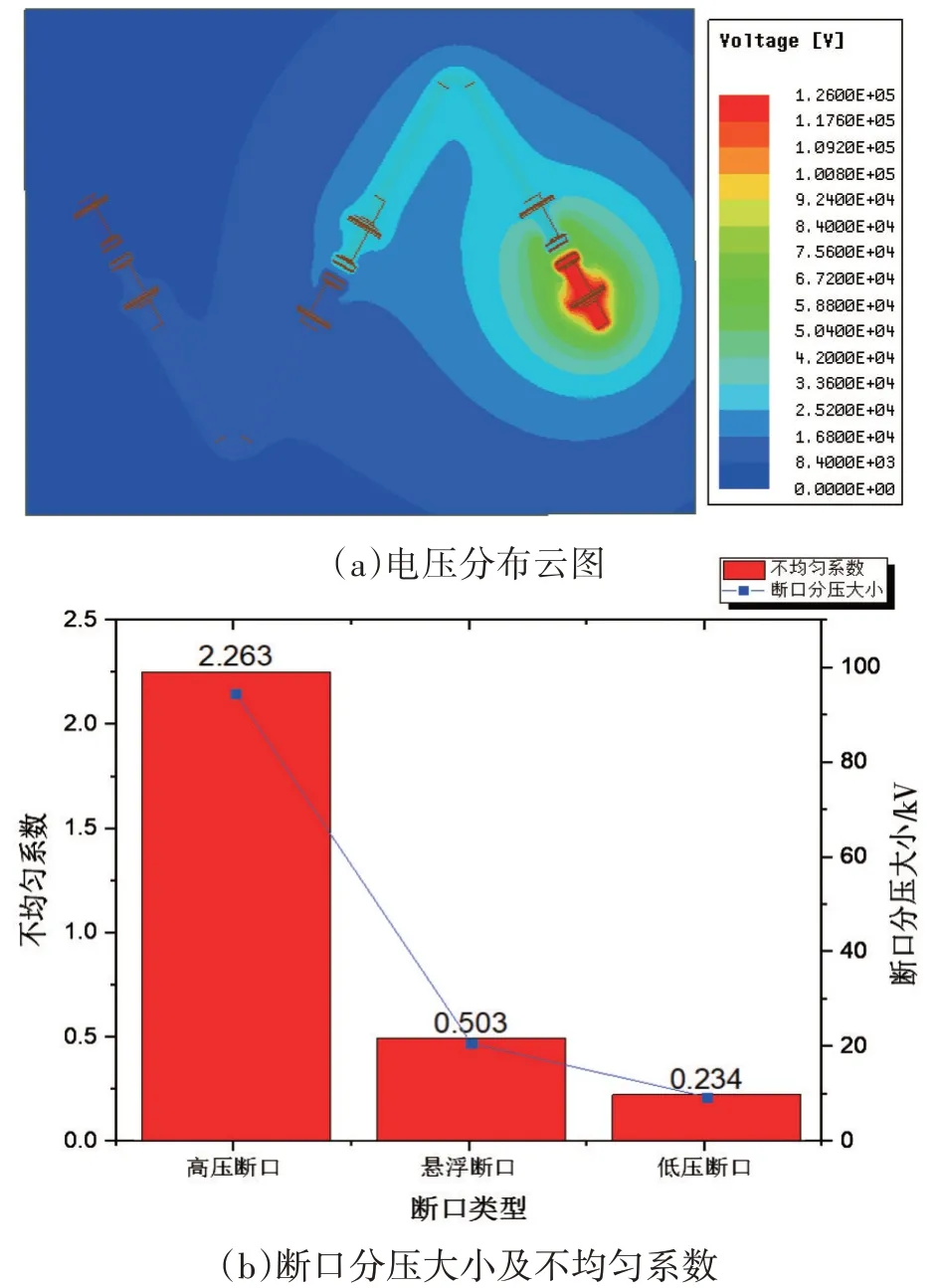
图2 断口电压分布及不均匀系数
图2(b)为计算得到的三个断口分压和断口不均匀系数,高压断口承担了近75.436%的电压,不均匀系数为2.263;悬浮断口承担了16.781%的电压,不均匀系数为0.503;低压断口承担了7.783%的电压,不均匀系数为0.234,由此可见在不并联均压电容的情况下,多断口真空断路器的断口分压是极不均匀的。
2.2 分布电容的分类及计算方法
Q3D 软件通过电容矩阵的方式可以得到导体之间全部的等效分布电容,仿真模型如图3 所示。1号灭弧室为低压断口灭弧室,2号灭弧室为悬浮断口灭弧室,3号灭弧室为高压断口灭弧室。
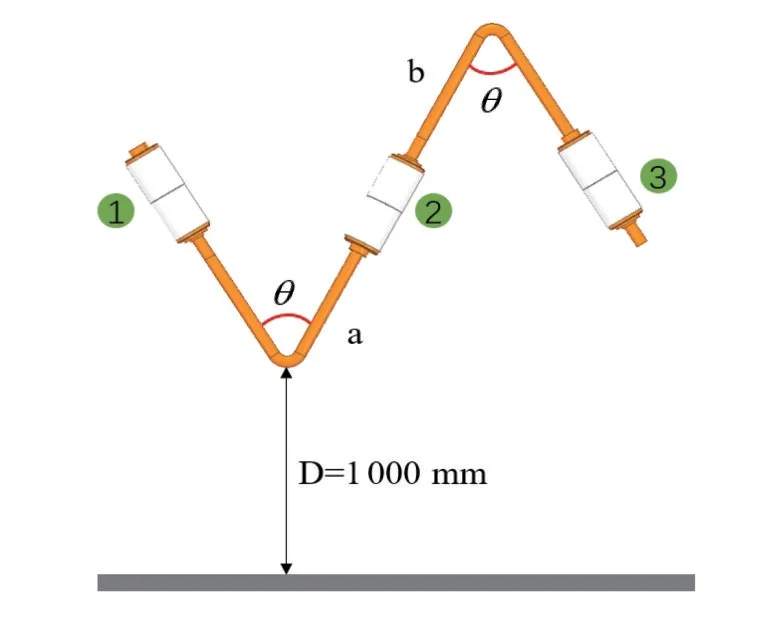
图3 126 kV三断口真空断路器Q3D仿真模型
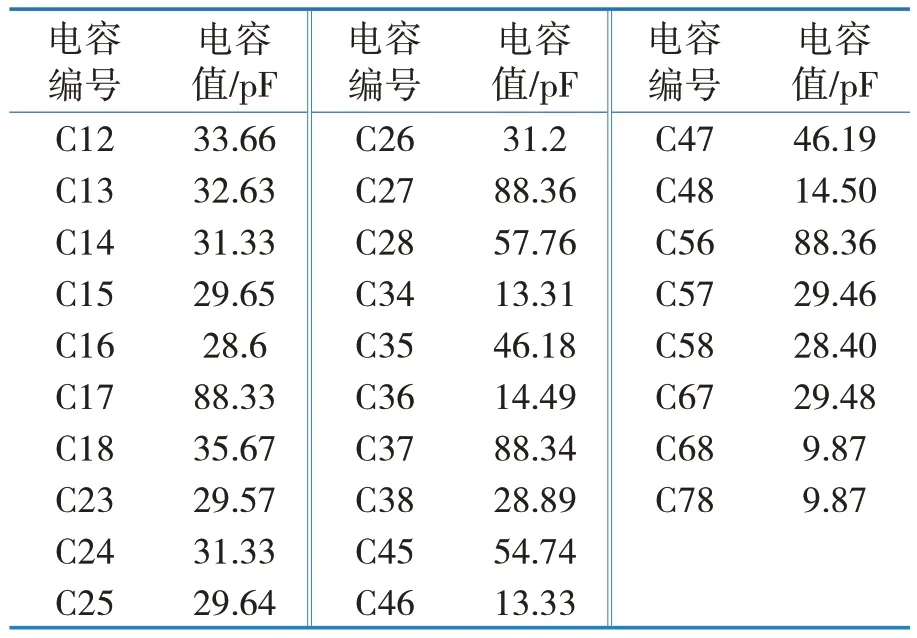
表1 126 kV三断口真空断路器分布电容参数
可以将电容矩阵的分布电容分为三类:第一类是灭弧室自电容,该类电容是由灭弧室本身的结构决定的,改变灭弧室的布置方式不会影响到该类电容的值的大小;第二类电容为对地杂散电容,该类电容是导体与大地之间存在的电容;第三类是结构杂散电容,该电容是由断口与断口间、母线之间存在电容。将电容矩阵中的电容按照三类分布电容进行计算,得到三类电容的数值大小,如图4所示。
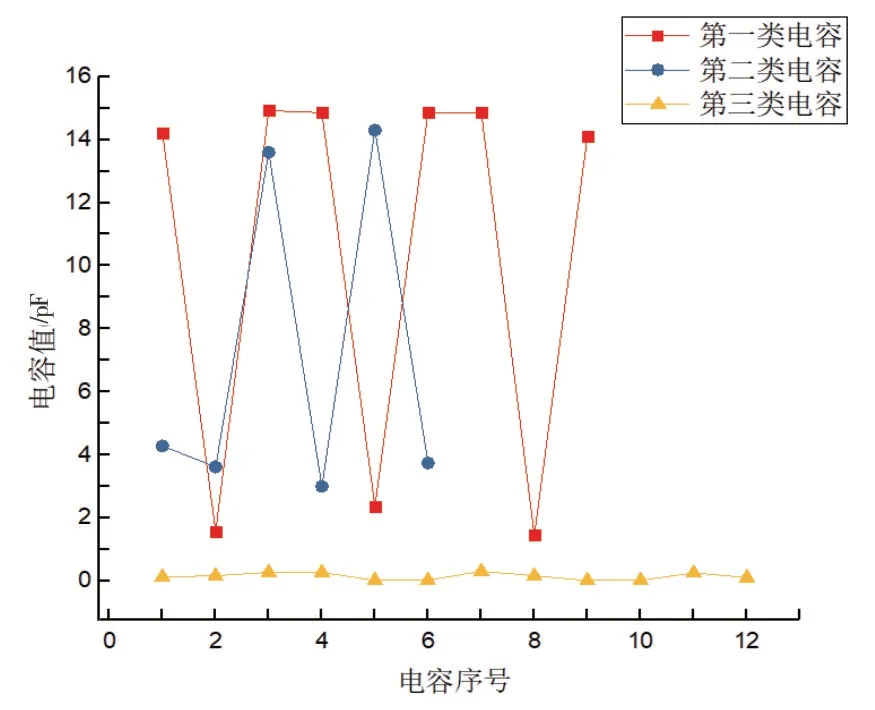
图4 三类分布电容值
由图4可知:第一类电容值集中范围为0~15 pF,第二类电容值集中范围为0~0.5 pF,第三类电容值集中范围为0~15 pF。可以看出第一类和第三类电容值相近,但是第二类电容的电容值相差甚远。
3 不同类型分布电容对断口电压分配的影响
为探究电容类型的不同对静态电压分配的影响,建立了含有不同电容类型的拓扑结构。如图5在Matlab/simulink 里搭建了三断口真空断路器的全电容等效模型,从左至右依次为第一类电容,第二类电容,第三类电容。当施加电源为126 kV时,通过与断口并联的电压表可以得到3个断口的断口电压。

图5 126 kV三断口真空断路器全电容拓扑
为了验证该拓扑的正确性,将第二节仿真计算的断口电压分布与该拓扑进行相互验证,如图6所示。可知两种方式下计算出的断口电压分布差距低于1%,因此可以判断该拓扑的正确性。
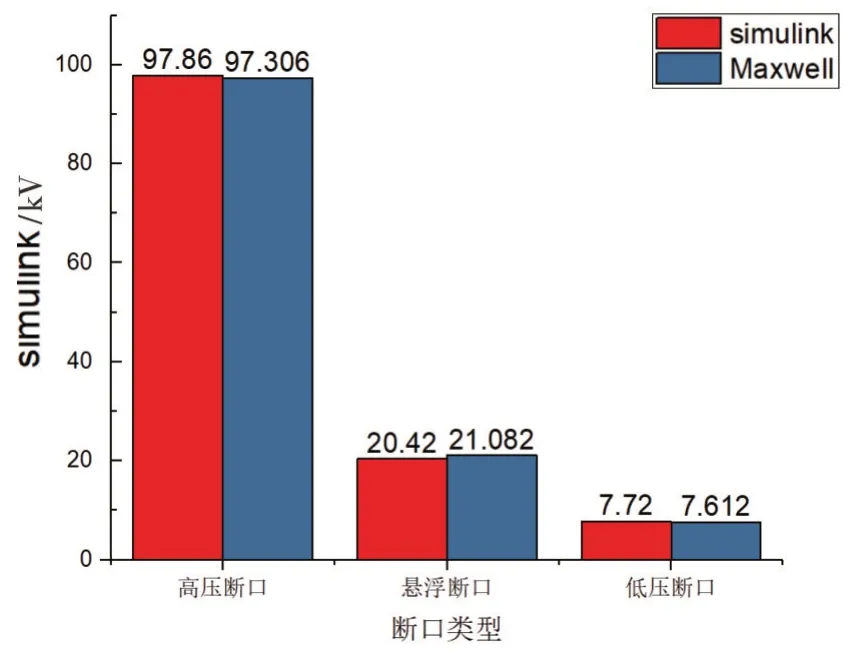
图6 全电容拓扑与有限元仿真相互验证
为研究每种分布电容对断口电压分布影响,考虑四种包含不同分布电容类型的组合,分为组合1(第一类电容)、组合2(第一类电容和第二类电容)、组合3(第一类电容和第三类电容)、组合4(第一类电容、第二类电容和第三类电容)。建立不同分布电容组合的拓扑,将第二节计算得到的分布电容值代入到每一种组合的拓扑中,图7 所示为组合2的拓扑结构。
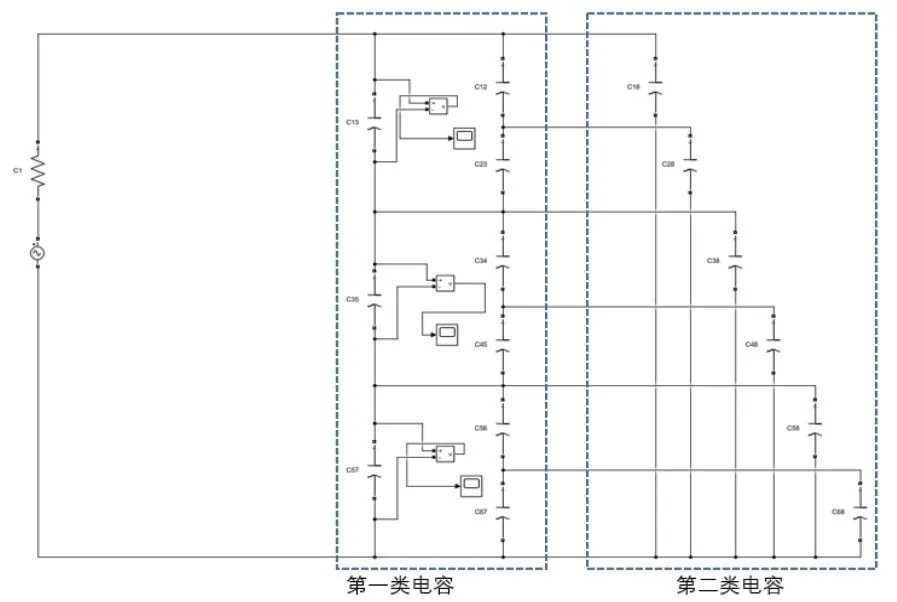
图7 组合2拓扑结构
当施加电源为126 kV 时,通过断口并联的电压表可以得到3个断口的断口电压,如表2所示。
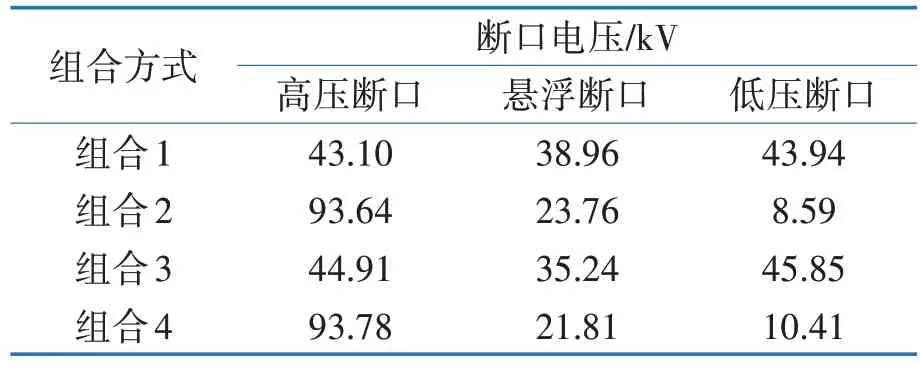
表2 4种组合方式下断口电压分布
为了研究每一种分布电容类型对断口分压产生的影响,采用控制变量法来分析每一类分布电容类型对断口分压产生的影响。
由图8可知,在不引入对地杂散电容之前,三个断口的断口电压不均匀系数在0.9~1.1之间,当引入对地杂散电容后高压断口不均匀系数由1.03变为2.23,高压断口的断口电压不均匀系数变化率为116.5%;悬浮断口不均匀系数由0.93 变为0.57,悬浮断口的断口电压不均匀系数变化率为-38.7%;低压断口不均匀系数由1.05 变为0.2,低压断口的断口电压不均匀系数变化率为-81%。故存在灭弧室自电容时,引入对地杂散电容会使得3个断口的断口分压变的极不均匀。
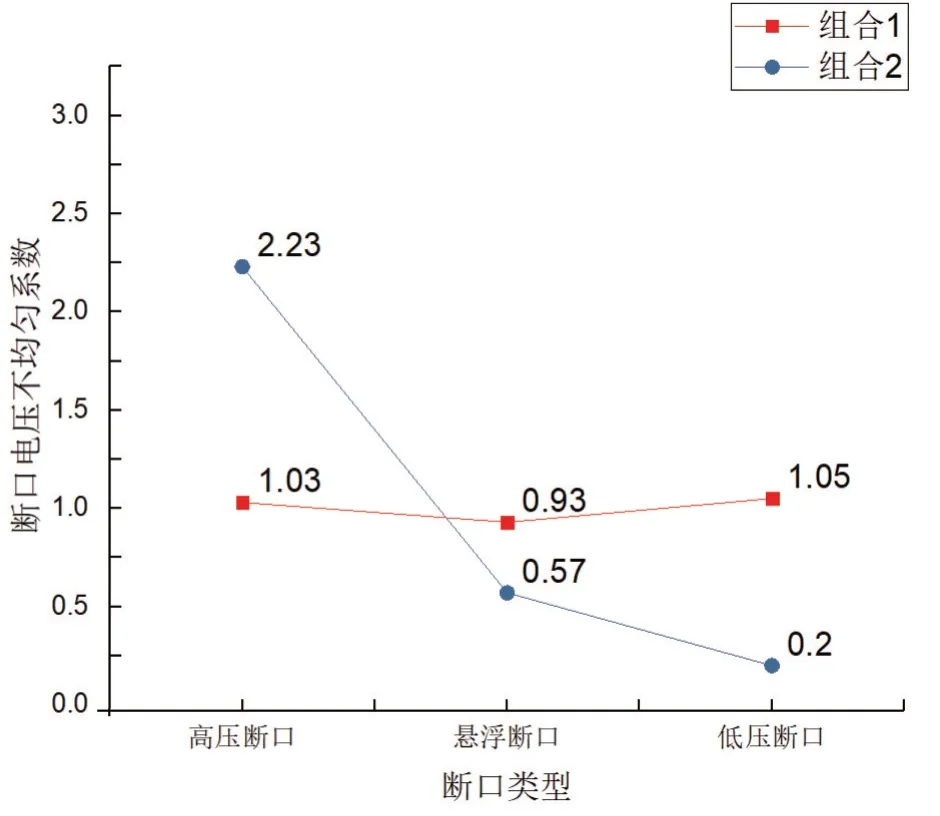
图8 组合1和组合2的断口电压不均匀系数对比
由图9 可知相比于组合1,由于组合3 引入了结构杂散电容,高压断口的不均匀系数由1.03 升高至1.07,高压断口的断口电压不均匀系数变化率为3.88%;悬浮断口的不均匀系数由0.93 降低至0.84,悬浮断口的断口电压不均匀系数变化率为-9.68%;低压断口的不均匀系数由1.05 升高至1.09,低压断口的断口电压不均匀系数变化率为3.81%。可知引入结构杂散电容后,3 个断口的断口电压均匀程度均降低。
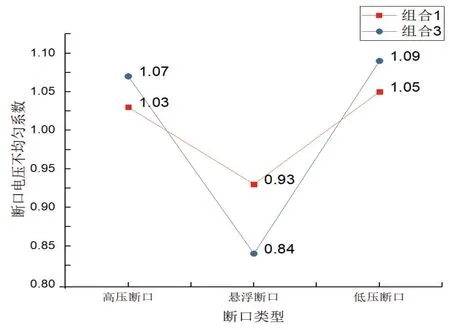
图9 组合1和组合3的断口电压不均匀系数对比
由图10 可知,相比于组合2,组合4 引入了结构杂散电容,结构杂散电容的引入使得高压断口的不均匀系数由2.229 升高至2.233,高压断口的断口电压不均匀系数变化率为0.18%;悬浮断口的不均匀系数由0.57 降低至0.52,悬浮断口的断口电压不均匀系数变化率为-8.77%;低压断口的不均匀系数由0.2 升高至0.25,低压断口的断口电压不均匀系数变化率为25%。当灭弧室自电容和对地杂散电容存在时,引入结构杂散电容会使高压断口和低压断口的电压分布稍微均匀,但会使得悬浮断口的电压分布稍微不均匀。
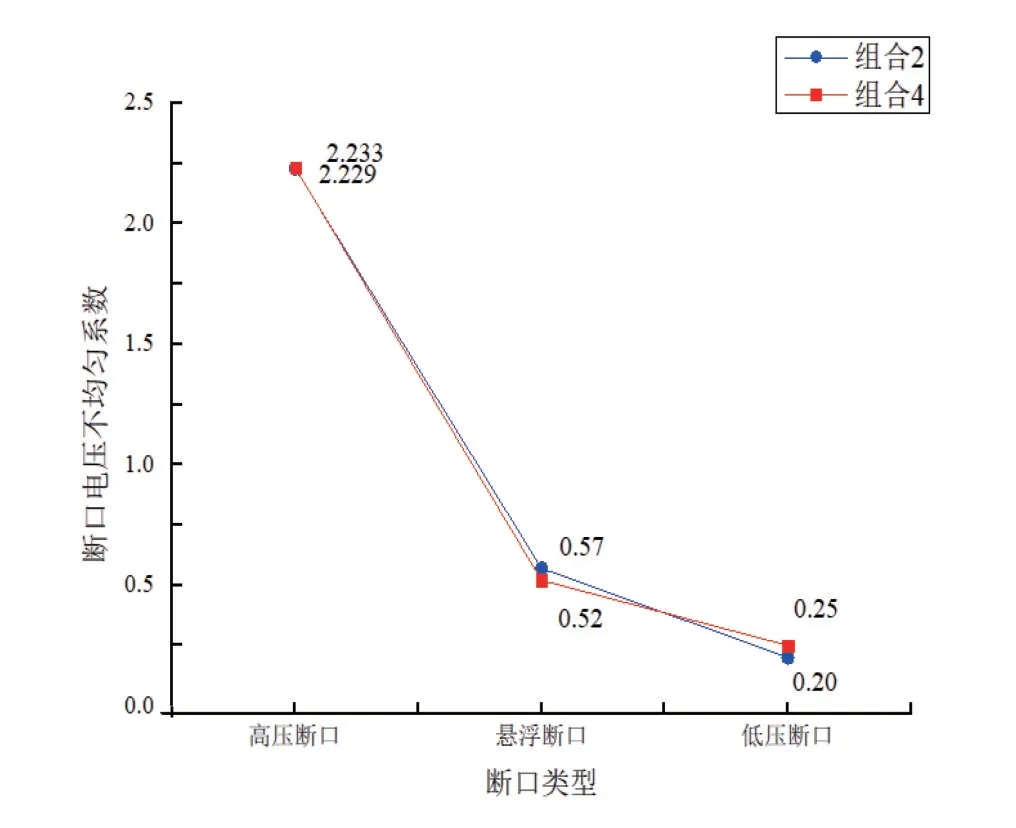
图10 组合2和组合4的断口电压不均匀系数对比
由图11 可知相比于组合3,组合4 引入了对地杂散电容,对地杂散电容的引入使得高压断口的不均匀系数由1.07 升高至2.23,高压断口的断口电压不均匀系数变化率为108.4%;悬浮断口的不均匀系数由0.84 降低至0.52,悬浮断口的断口电压不均匀系数变化率为-38.1%;低压断口的不均匀系数由1.09 降低至0.25,低压断口的断口电压不均匀系数变化率为-77.1%。可知当灭弧室自电容和结构杂散电容存在时,引入对地杂散电容会使得3个断口的断口电压分布变得极不均匀。
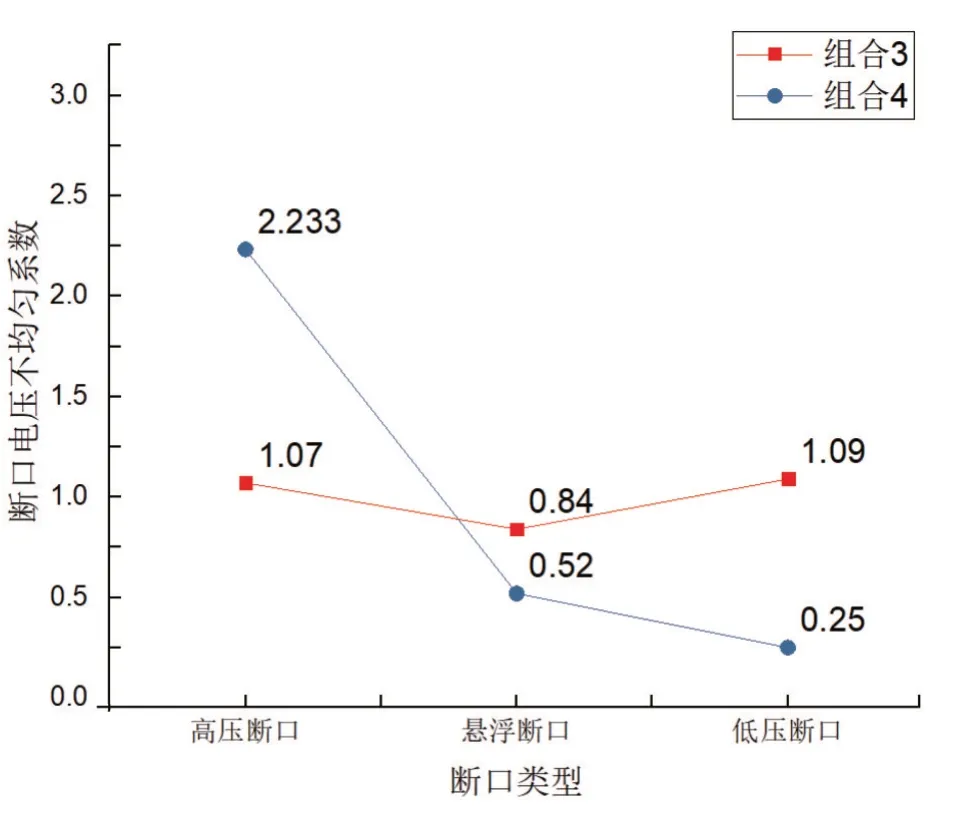
图11 组合3和组合4的断口电压不均匀系数对比
定义分布电容对断口电压不均匀系数改变率:

式中:n2—该类分布电容引入后,断口的不均匀系数;
n1—该类分布电容引入前,断口的不均匀系数。
由图12 可以看出,当存在结构杂散电容时,对地杂散电容的引入对三类断口的断口电压不均匀系数变化率会更低。当仅存在自电容的时候,引入对地杂散电容后高压断口的断口电压不均匀系数变化率为45%,而存在自电容和结构杂散电容时,引入对地杂散电容后高压断口的断口电压不均匀系数变化率仅为16%。
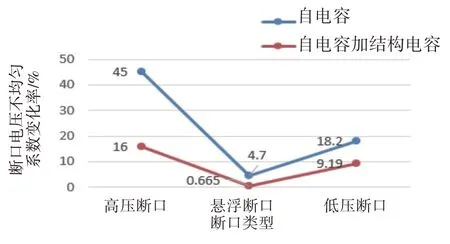
图12 引入对地杂散电容对不均匀系数变化率的影响
由图13 可以看出,当存在对地杂散电容时,结构杂散电容的引入对三类断口的断口电压不均匀系数变化率会更低。仅存在自电容的时候,引入结构杂散电容后高压断口的断口电压不均匀系数变化率为1.625%,而存在自电容和对地杂散电容时,引入结构杂散电容后高压断口的断口电压不均匀系数变化率仅为0.0027%。
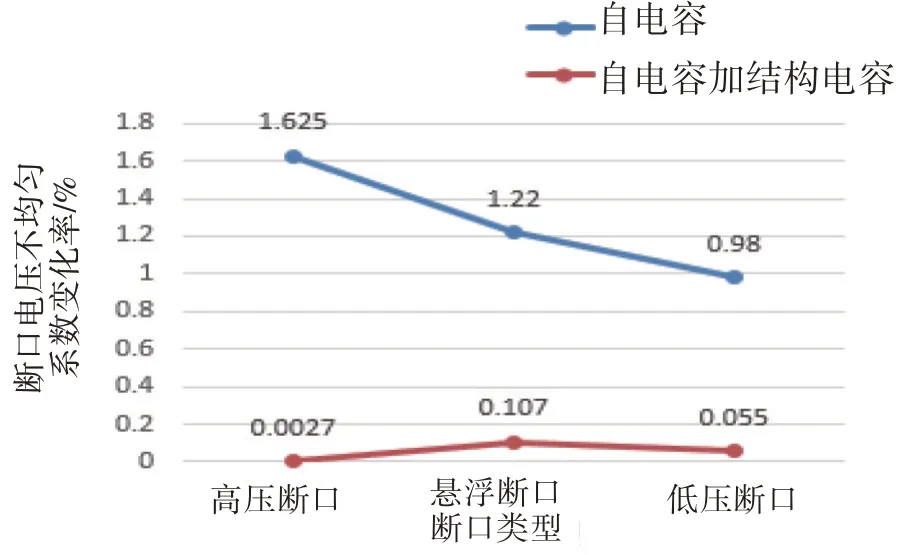
图13 引入结构杂散电容的影响
4 不同排列方式的影响
4.1 不同排列方式下断口电压分布特性
为了研究排列方式对断口电压分配的影响,首先定义相邻断口母线夹角为θ,θ取值为60°,90°和120°。通过ANSYS Maxwell 静电场仿真得到静态电压分布。图14为三种夹角下的断口电压分布。
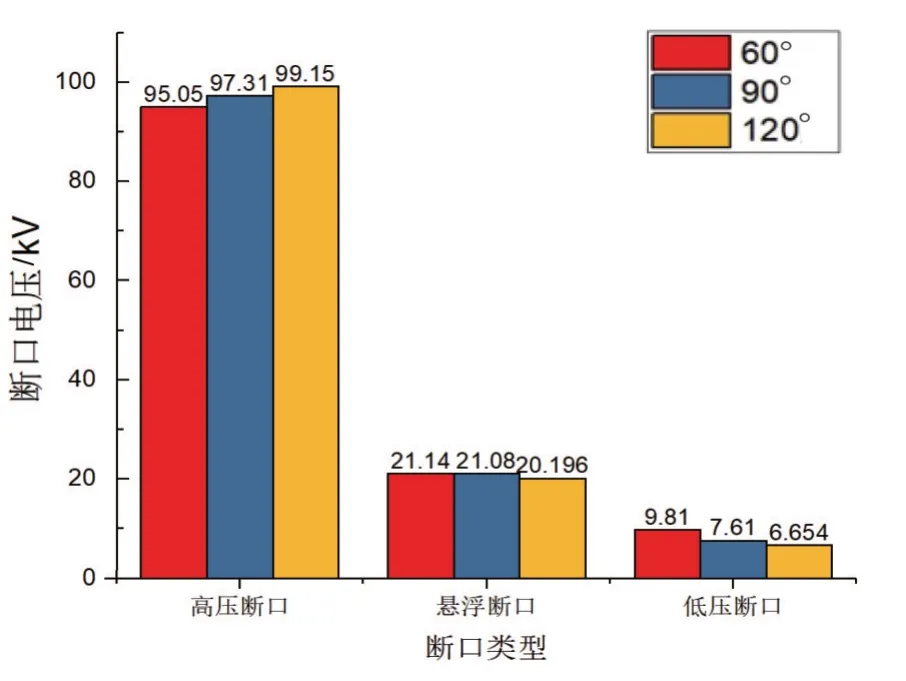
图14 3种夹角下各断口电压分布
由图14可知,随着夹角的增大,高压断口的断口电压逐渐增大,从95.05 kV 增大到99.15 kV,增幅为4.31%;悬浮断口的断口电压逐渐减小,从21.14 kV 减小至20.196 kV,增幅为-4.47%;低压断口的断口电压逐渐减小,从9.81 kV 减小至6.654 kV,增幅为-32.17%。
4.2 不同排列方式对不同类型分布电容的影响
由于每一类分布电容的种类较多,在三类电容中选取具有代表性的电容来说明排列方式对不同类型分布电容的影响。第一类电容中选取C13,C35 和C57。第二类电容中选取C28,C48 和C68。第三类电容中选取C24,C26和C46。
表3 列出了3 种不同的夹角下,选取的9 个典型分布电容的大小。
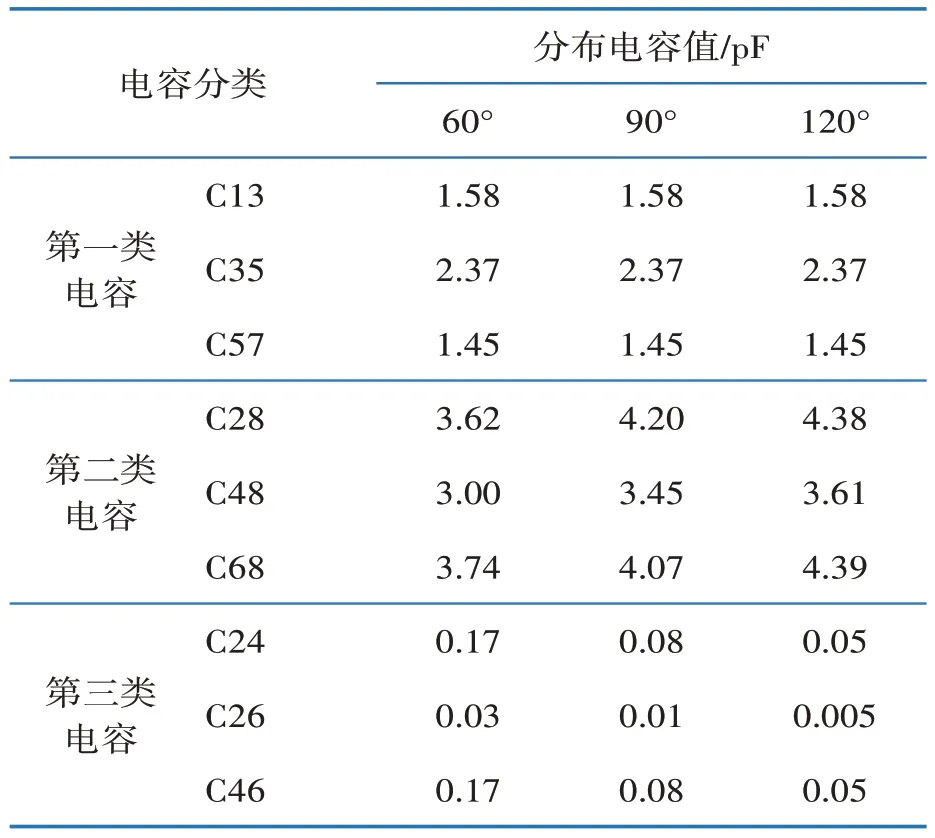
表3 3类分布电容在3种夹角下的典型值
由表3可知,随着夹角的增大,第一类电容的电容值保持不变,第二类电容的电容值逐渐升高,第三类电容的电容值逐渐降低。
4.3 总体影响
不同设计结构的参数均会对真空断路器电容分布及断口电压分布产生影响。因此,在排列方式确定后,结合对电容的影响,可针对性地将三类分布电容进行优化,实现性能的最优解。
5 结论
采用有限元法对V型排列的126 kV三断口真空断路器的电位分布进行计算,并利用表面电荷法对断路器整体的分布电容进行了计算,然后将断路器分布电容分类。通过将不同类型的分布电容进行组合,分析不同类型电容对断口电压分布的影响,最后通过改变V型排列夹角,研究夹角变化对断口电压分布和三类分布电容的大小影响,得出主要结论:
1)126 kV三断口真空断路器在未并联均压电容时,三个断口的分压极不均匀,按照分布电容将三断口真空断路器的分布电容分为三类,即灭弧室等效自电容、对地杂散电容和结构杂散电容。
2)当只考虑灭弧室等效自电容时,高压断口,悬浮断口和低压断口的断口电压不均匀系数分别为1.03,0.93和1.05。
3)当灭弧室等效自电容存在时,对地杂散电容的引入会使得高压断口,悬浮断口和低压断口的断口电压不均匀系数分别由1.03,0.93和1.05变为2.23,0.57和0.2。
4)当灭弧室等效自电容存在时,结构杂散电容的引入会使得高压断口,悬浮断口和低压断口的断口电压不均匀系数分别由1.03,0.93和1.05变为1.07,0.84和1.09。
5)仿真结果表明结构杂散电容和地杂散电容均会对另一类分布电容对断口电压均匀度的破坏起到抑制作用。
6)随着V型排列方式下的夹角的增大,高压断口、悬浮断口和低压断口的断口分压不均匀系数逐渐升高,即断口分压变的更加不均匀,灭弧室等效自电容的电容值保持不变,对地杂散电容的电容值逐渐升高,结构杂散电容的电容值逐渐降低。
