三轴转动惯量的振复摆与扭摆法协同测量比例法

杨洪涛, 卢志辉, 孙浩智, 武艺泳, 刘珉, 来颜博

(郑州机械研究所有限公司, 河南 郑州 450052)

0 引言

三轴转动惯量的测量需要对应3个姿态方位进行圆周摆动,或者以其他体现圆周运动加速度因素的方式运动,3个位姿摆放常常给测量带来一定的困扰。扭摆法和复摆法都属于常用的转动惯量测量方法,这两种方法具有不同的结构和对应的摆动方程以及各自应用特点。扭摆法更为经典,是业界通用的测量方法,是基于直立轴系和扭摆弹性单元实现圆周摆动运动,通过测量扭摆周期并与标准样件的摆动周期进行比对计算各个转动惯量分量。复摆法为水平轴系,基于被测体重力与直立振动单元形成摆动来测量对应方位的惯量值,一般还需要移轴处理得到自身转动惯量值,移轴计算由于质心位置偏离过大,很难精确测定而带来粗大误差。

位姿调整多数直接采用与外形相适应的工装支撑,也有采用多维空间转动框架支撑的。前者结果可靠,但操作繁琐,支撑工装种类多。后者测量过程便捷,但机构复杂、皮重大,运动副存在的间隙对摆动运动造成干扰;某些带翼异形体在翼展方位往往很难实现与测量设备的支撑连接。因此,解决位姿影响需要新的思路与方法。

文献[1]提出了振复摆法与扭摆法相结合的协同测量方法(以下简称协同测量法),利用直立振复摆法建立起两个横向转动惯量分量之间的关系,再利用扭摆方法测量其中一个分量,从而减少一次水平状态下的姿态变化。该文献给出了基于两个横向转动惯量差值的协同测量方法(以下简称协同差值法),包括当量样件惯量法和当量刚度系数法。

协同测量法根据两个横向惯量之间的关系,还存在利用其比例关系测量与计算的方法(以下称协同比例法),为三轴转动惯量提供一种新的测量计算路径,尤其可以有效地回避带翼异形体翼展方位的支撑问题,解决了异形体三轴转动惯量的测量难题。

1 转动惯量协同比例法测量原理

1.1 扭摆法

扭摆法是转动惯量测量中采用的最经典的方法,其原理结构主要包括旋转摆动轴系和弹性单元,被测物体放置在与扭摆弹性单元固连的转台上,在外界的激励下做圆周摆动运动[2-5]。国内对其具体轴系形式结构(机械轴承、气浮转台)、测控系统、误差分析、设备标定及标准件赋值等方面都有一定的研究[3,6-11]。

设J为被测物体+系统对扭摆中心的转动惯量,K为扭摆弹性单元刚度系数,T为摆动周期。实际测量过程中,摆动系统受到的阻尼可以忽略,则有

(1)

即转动惯量J与摆动周期T的平方呈正比。实际测量过程中采用样件比对测量,依次测出转台摆动系统的扭摆周期Tte、标准样件+摆动系统的扭摆周期Tts(标准样件自身转动惯量为Js)、产品+摆动系统的扭摆周期Ttc,就可得出导弹弹头的转动惯量Jc为

(2)

1.2 直立振复摆法

复摆法[12-16]也是测量转动惯量的主要方法之一,由于被测体自身质心距离摆动轴线比较远,且难以精确测定,转动惯量的移轴计算会带来较大误差。文献[13]建立了采用振复摆法直接测量转动惯量的振复摆模型,推导了振复摆的计算公式,

空气阻尼忽略不计的情况下,有

(3)

式中:k为振复摆弹性单元刚度系数;L为弹性单元中心到振复摆中心的距离;m为被测体+摆动系统质量;g为当地重力加速度;h为被测体+摆动系统质心到振复摆中心的距离。

1.3 协同比例法

扭摆法和复摆法测量转动惯量两种方法均具有各自特点[2],扭摆法的测量误差比复摆法小,文献[2]认为测量的高不确定度是由测量装置精度因素造成的,而不是由测量原理造成的。文献[1]指出复摆法中摆动系统和被测物体高度难以精准测量,其造成的移轴误差是测量误差的主要来源。

图1为扭摆法和振复摆协同法机构示意图。图1中,h0为测量设备工装上平面到摆动轴线的距离,hc为被测体质心到复摆中心距离,xc为被测体质心到被测体下端面的距离。

在图1所示质心和转动惯量集成测量设备上,利用扭摆法精度高的优势,结合直立刀口振复摆确定两个分量之间的比例关系,可以在水平姿态下不翻转被测产品完成两个横向转动惯量的测量,被称为直立刀口振复摆和扭摆法协同测量比例法,为三维转动惯量测量提供了新的思路。

1.3.1 原理结构

直立刀口振复摆与扭摆协同测量原理结构示意见图1,图中示意的为直立工装的使用状态,主要包括主轴、主轴圆盘、刀口结构、中心扭杆及其紧固组件、支臂、板簧。被测物体通过直立工装或者水平工装固定在主轴的圆盘上,实现相关直立和水平状态特性参数的测量。主轴悬浮在一组刀口上面,与之垂直方向连接一组支臂,支臂和弹性元件板簧相连,组成直立刀口振复摆系统,该系统早期设计用于导弹弹头质心横偏高精度测量[17]和惯性积测量[18]。

由电机通过直立轴系驱动产品分别位于y轴、z轴方向,再由拨动机构使产品沿刀口摆动,测量复摆周期,以建立两个方位惯量分量之间的关系,同时可以利用结构中的圆周扭摆系统测量弹头轴向转动惯量的Jx。通过水平工装将产品水平放置在转台上,利用扭摆测量横向转动惯量Jy或Jz。

1.3.2 计算方法

对于式(3),令

Kd=2kL2-mgh

(4)

式中:Kd为振复摆系统的特性参数。记Ty和Tz为被测件+摆动系统y轴方向和z轴方向相对于摆动中心的摆动周期,预先将设备两个方向做初始周期平衡处理,则摆动系统在这两个方向上相对振复摆中心的转动惯量J0y等于J0z,统一记为振复摆系统的转动惯量J0,则结合式(3)、式(4)可以得到

(5)

取式(5)中两式做比值,可以推导出:

(6)

对于导弹弹头这类回转体,通常Jy和Jz理论值一样大,实测出非常接近,其比值几乎为1,Ty和Tz也非常接近,因此近似有

(7)

式(7)是式(6)在Jy和Jz非常接近时的简化计算,仅适用于二者数值接近的情况。式(7)和式(6)中的两个表达式是等价的,在产品测量中一般选用容易测出的转动惯量作为自变量。

2 协同比例法相对于扭摆法误差分析

本文测量的基础是基于扭摆法,主要分析与扭摆法精度的差异。

将(6)式代入,有

(8)

式(8)第1项为协同测量比例法带来的附加误差,第2项等同于扭摆法的原始误差。

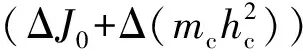
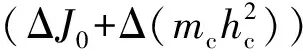
表1 协同比例法引起的附加误差值

表2 4组模拟件基本参数和三轴转动惯量扭摆法测量结果

表3 设备及4组模拟件基础数据

3 实验方法与实验结果

3.1 实验方法

本文测量的基础是基于扭摆法,采用圆周摆动方法测量得到Jx、Jy,再由立式振复摆测量Jy、Jz之间的关系,最后得到三轴分量。最终的测量精度取决于扭摆法,因此以下实验结果就直接以扭摆法结果为比较基准,这样就可以采用没有理论值的工件模拟实际产品进行实验测试了。

如图2所示,设计为锥形哑铃状模拟产品,前后两个锥形圆盘放置在水平工装上测量Jy、Jz,直立状态大圆盘放置在直立工装上测量Jx扭摆法周期、Jy和Jz的直立振复摆周期。同时通过在模拟件上沿z轴方向布置大小不同的两组试块和翼展模拟组件,改变其惯量值,进行多组实验测量。

图2 模拟产品、模拟产品+第1组试块、模拟产品+第2组试块、模拟产品+翼展模拟组件实验状态示意图Fig.2 Schematic diagram of experimental state of simulated product, simulated product+the first group of test blocks, simulated product+the second group of test blocks, simulated product+wing unfolding simulation components

首先在集成测量设备上测量模拟件的质量特性参数,包括质量、轴向质心、横向质心、三轴转动惯量。转动惯量采用扭摆法测量,并作为比较基准。测量3次数据取其均值。

再依次测量摆动系统振复摆周期T0、模拟件+摆动系统y轴方向、z轴方向振复摆周期Ty、Tz,以及模拟件+试块(或翼展组件)+摆动系统y轴、z轴方向振复摆周期T′y、T′z,每组测量周期5次并取均值,利用4组数据进行相关计算与分析。实验设计4组,其中1组为模拟产品原始状态,2组为人为增加不同试块造成两个方向转动惯量具有较小差值,1组为人为增加翼展模拟组件配重造成两个方向转动惯量具稍大差值,以考察Jy/Jz比值分布对该方法精度的影响和协同比例法的可行性。

3.2 实验结果

3.2.1 扭摆法测量结果

测量结果见表2。表2中质量、轴向质心位置用于转动惯量移轴计算,三轴转动惯量数据Jy、Jz作为最终测量结果,Jy用于与协同比例法结果进行比对,考察附加误差情况。其中表2中的轴向质心数值为实验模拟件质心到上端面的距离。

3.2.2 测量设备基础数据确定

测量计算需要用到测量设备相关的基础数据,包括振复摆系统和工装相对于摆动轴线的惯量值J0、被测体质心到摆动轴线的距离hc,hc=xc+h0。

J0由三维建模,按照理论密度进行仿真求得每个工件的值,再由单件实际称重值进行修正。xc由实验设备测出,具体是实验用模拟件高度与轴向质心数值的差值,模拟件高度经实际测量为973.5 mm,h0为实验设备实际测量得出。具体结果见表3。

3.2.3 协同比例法测量结果

分别测量模拟件+摆动系统y轴方向的振复摆周期Ty、模拟件+摆动系统z轴方向的振复摆周期Tz,计算得到转动惯量协同比例法测量值,再与扭摆法测量值比较得到误差值。两组采用模拟件的实验测量数据见表4、表5。

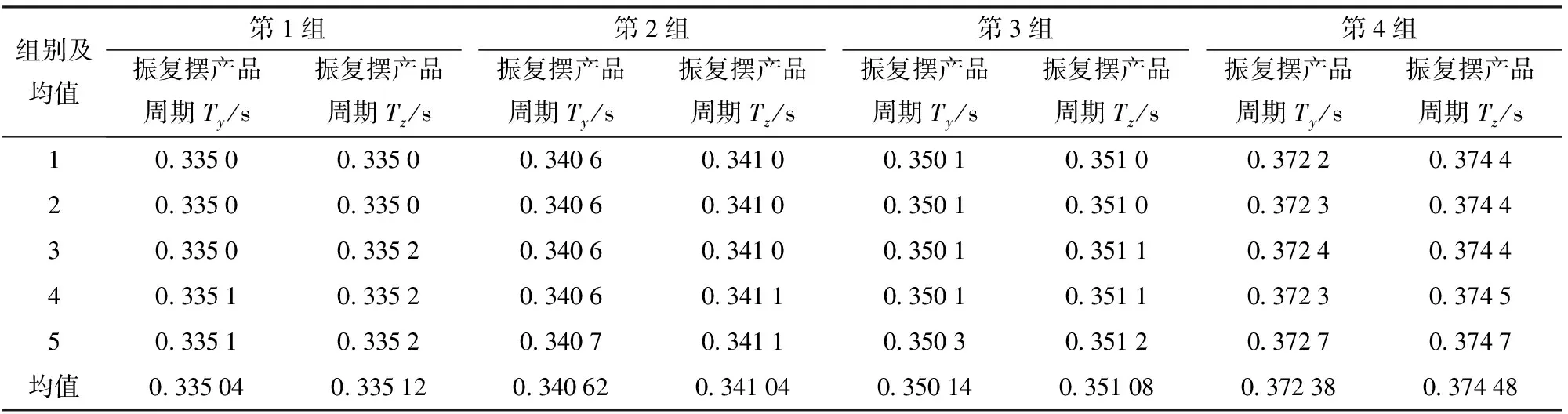
表4 4组模拟件周期协同比例法测量结果

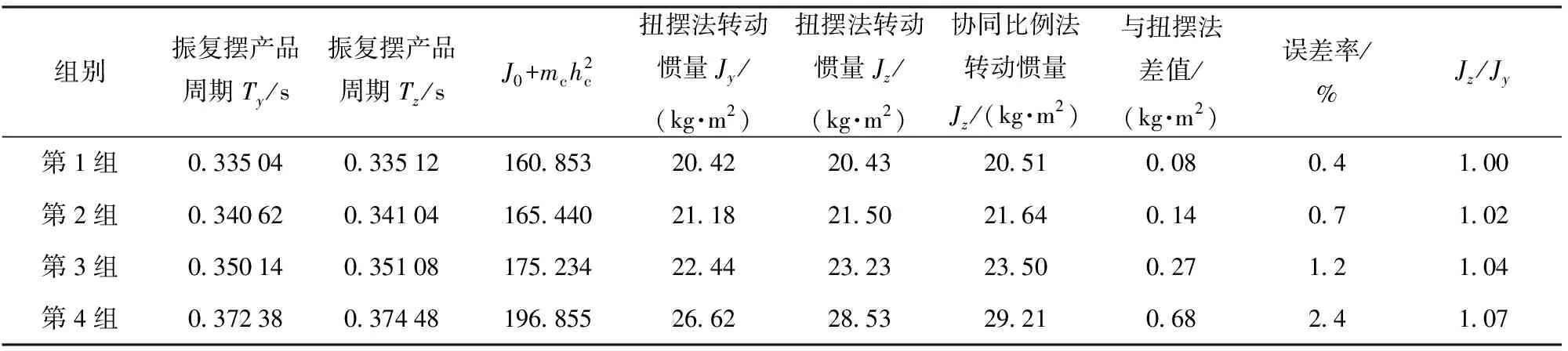
表5 4组模拟件转动惯量Jz协同比例法测量结果

模拟实验件和设备均是利用现有的条件进行的,由于当前条件的约束,实验件Jy/Jz的数据分布范围偏窄,但是与大多数实际异形体分布基本匹配,也达到了对方法进行验证的目的。

从表5中数据可以看出:1～4组数据绝对误差与误差率增加明显,在Jy与Jz接近时,二者测量结果比较接近,Jz/Jy小于1.02时,误差率小于1%,随着比值增加,误差几乎呈线性增加;最大绝对测量误差值为0.68 kg·m2,最大误差率为2.4%,高于机械转台通常采用扭摆法的惯量测量误差率0.5～1%的测量精度。但是对于带翼异形体在翼展方向无法支撑的情况,这个测量精度是可以接受的,而且测量无需新增专用工装,实施便捷。

3.3 近似计算与全因计算对比

比较式(6)和式(7)并进一步考察式(8),对应地可以看出式(6)的第2分项即为类似扭摆法线性关系部分,对应式(8)中的第2项误差等同于扭摆法的原始误差;式(6)的第1分项则为摆动系统本身因Jy与Jz不同引起的固有惯量值,对应式(8)中的第1项无法消除的附加误差。

按照式(7)计算Jz数据及对比结果见表6,从中可见误差率在Jy与Jz基本相等时,二者结果是一致的,此时轴系加工装系统的惯量值对测量精度没有影响;在Jz/Jy小于1.02时,二者误差不大,随着Jz/Jy比值增加,近似计算法误差增速明显更快。

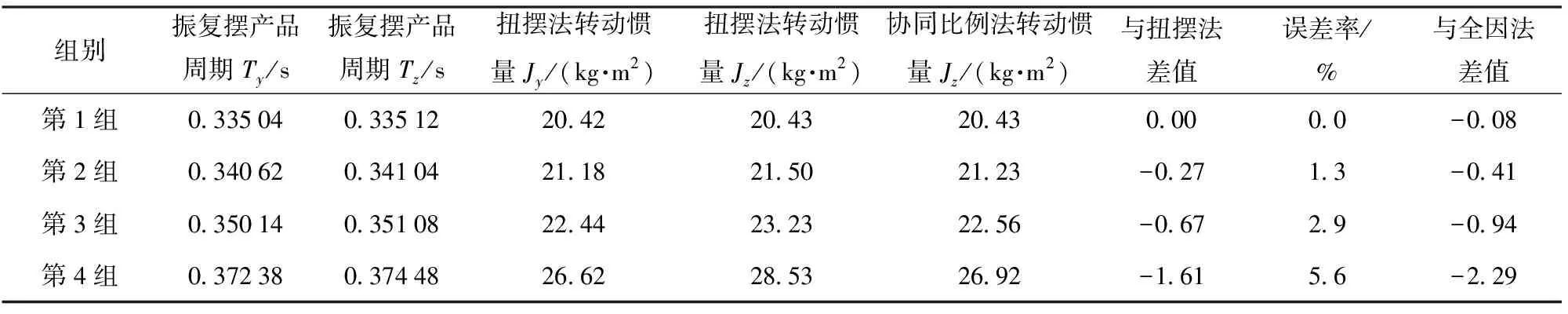
表6 4组模拟件协同比例法近似计算结果

综上可以看出,对于回转体弹头,近似计算法就能满足测量精度要求,对于带翼异形体,协同测量比例法更为适宜,其比值界限定在1.02比较合适。

4 协同测量法应用分析

本文提出的协同比例法,直接采用模拟件作为被测体,测量过程与实际弹头类或带翼飞行体完全相同,其结果可以考核协同比例法的实际应用效果。模拟件因保密与实际飞行体在质量及外形方面均有一定差异,比产品质量更轻导致与测量系统参数匹配性更差,增大了测量误差,实际产品测量精度比模拟件精度更高。

文献[1]提出了协同测量差值法(具体分为当量刚度系数法和当量样件惯量法),本文新提出了协同测量比例法。这两种方法已被实验验证和实际应用证明是有效的、可靠的,但是也存在不同的适用范围。

具体分析,对于定型设备,测量对象稳定单一,采用协同测量差值法精度高、使用便捷,文献[1]显示,9次测量中,最大误差率0.63%,其余误差率多在0.5%及以下,不超过机械结构转台测量误差率0.5%～1%的测量精度,应为首选。当然采用协同比例法也是可行的,其测量误差增大0.5%左右。

在Jy与Jz基本相等的情况下,采用协同比例法中的近似计算法精度比协同差值法略低,但不需要针对性的标定,这样对于被测产品种类较多的情况,首选协同比例法。在Jz/Jy大于1.02的情况下,协同比例法中的全因计算法更适合产品测量。

协同比例法全因计算公式理论上适合任何情况,与协同测量其他方法相比,更适合于Jy与Jz具有一定差异的状态,此时精度略低于扭摆法。随着Jz/Jy增加,其误差相应增大,但是仍在合理范围内,具有较好的精度,对解决带翼异形体三轴转动惯量测量位姿转换问题提供了新的有效技术路线。

采用上述测量方法研制了5种规格共计9套测量设备,根据不同的使用特点分别采用了协同差值法和比例法(包括全因计算和近似计算),对于样件与模拟件检测结果均满足任务书要求,已交付3套投入实际测量。

早期本单位提供给部队、军工院所和相关工厂的同类型设备50余套,具有刀口板簧结构(产品旋转一周,通过测量质心沿刀口的摆动幅度确定质心位置)、圆周扭摆结构(测量转动惯量),具备实施协同测量的结构条件。通过软件更新并增加刀口复摆拨动机构即可升级到不同的协同测量方法。目前已改造部队某基地的质量特性测量设备,其Jy与Jz基本相等,具体采用了协同比例法中的近似法计算,成功避免了水平姿态需要人工辅助转动90°的繁琐操作。改造了一套异形体测量设备,对数据采用协同比例法全因素计算,其Jz/Jy约为1.05,取得了理想结果。

5 结论

本文在前期提出直立振复摆与圆周扭摆协同测量技术(协同差值法)的基础上,进一步提出三轴转动惯量测量的协同比例法,推导出了相应全因计算公式和近似计算公式并进行了误差分析,采用模拟件进行了相关验证实验,对协同测量法的应用场景进行了全面深入的分析。得出以下主要结论:

1)实验结果表明协同比例法测量具有效性和可靠性,Jz/Jy小于1.02时,全因计算公式和近似计算公式精度基本相当;Jz/Jy大于1.02时,采用全因计算公式更为适宜。

2)协同比例法简洁可靠,便于操作,已用于多个型号测量设备研发,成功用于回转体和带翼异形体的三轴转动惯量测量。

3)协同差值法适合于Jy与Jz基本相等的状态,测量精度较高,可媲美扭摆法,非常适用于专用定型设备;协同比例法近似计算公式使用场景与协同差值法一致,精度略低于扭摆法,适用于兼容多产品测量的设备;协同比例法全因计算公式能够满足Jy与Jz具有一定差异的状态,精度亦略低于扭摆法,是目前带翼异形体三轴转动惯量较适宜的测量方法。