基于推理能力发展的数学例题教学研究
2023-05-30尤维明
尤维明


[摘 要] 《义务教育数学课程标准(2011年版)》中,将推理能力作为数学核心素养的六要素之一,由此确定了推理能力的重要地位. 文章以一道关于圆的综合题的教学为例,从解题障碍成因分析出发,具体从以下几方面展开讨论:初步审题,找出有价值的信息;紧扣目标,确定解题的突破口;验证猜想,促进推理能力发展;画图分析,凸显图形依赖关系;及时反思,积累解题经验.
[关键词] 推理能力;例题教学;圆;解题经验
史宁中教授提出:抽象、推理、模型是数学发展所依赖的主要思想,其中,推理能力的培养不能脱离具体的教学活动的支撑[1]. 良好的数学推理能力形成于知识的学习过程,数学思想方法的渗透过程以及数学问题的解决过程中,学生在教师的引导下逐步积累、领悟、内省而形成各种能力. 至于教师“教什么”“怎么教”对学生的个人发展有着直接影响.
例题教学是数学教学的重要组成部分,然而在现实教学中却有部分教师存在“重解题,轻过程”的行为,淡化了对学生数学推理能力的培养意识. 其实,通过对问题的观察、思考、拓展不仅能帮助学生领悟解题的要领,更重要的是能培养学生的数学推理能力.
原题呈现
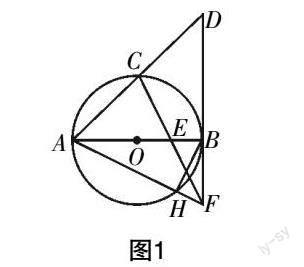
如图1所示,AB为☉O的直径,点C为圆弧AB的中点,BD为☉O的切线,交AC的延长线于点D,点E为OB的中点,CE的延长线与切线BD相交于点F,AF与☉O相交于点H,连结HB.
(1)求证:AC=CD;
(2)如果OB=2,求HB的长.
学生在自主解题过程中,主要存在以下几个问题:①只能根据已知条件提炼出部分简单结论;②思维卡壳,不会求BF的长;③因为不会求BF的长,就凭借直觉猜想∠FAB=30°,并应用该猜想进行推理,形成错误结论;④虽然正确解题,但在添加辅助线(连结OC)上花费了过多时间.
本班学生的认知属于中等偏上的水平,学生在解决本题过程中所暴露出来的问题具有典型性. 结合学生的认识水平与解题状况的分析,可以看出不同层次水平的学生在推理能力上有着显著差异,这也给笔者带来了一个启示,即面对有一定难度的关于圆的综合问题,学生的解题思维需要经历一个复杂且曲折的过程,而非一气呵成那么简单.
本题解题障碍的成因分析
1. 题目本身综合性高
一般情况下,关于圆的综合类问题的设计,常以圆为整个问题的背景,综合考查学生对几何知识的掌握程度,对学生的几何直观能力、推理能力以及运算能力的要求较高,同时还要考查学生解题过程中对数学思想方法的领悟与应用,并对几何模型的建构提出了要求.
观察本题,发现题目不仅涉及与圆相关的各种概念,如直径、弦、弧与切线等,还应用到各种原理,如圆周角定理、切线性质、全等三角形的判定定理、等腰三角形的判定定理与性质以及勾股定理等. 学生只要对其中一个定理理解得不够透彻,就会影响整道题的解决效果. 由此可见,本题的综合程度高、考查范围广.
2. 学生解题思维受限
解题过程中,运算会遵循通用的运算法则,程序化的运算特征使得学生遇到运算类问题时有章可循. 然而,综合性高的几何问题,学生很难从大脑中提取到程序化的通用解题模板,这就需要學生在题目条件与结论之间建构桥梁,不断调整解题思路,找出其中的联系[2].
调整解题思路的过程,并非顺流直下或逆流而上的过程,而是不断观察、分析、推理的过程,这就需要学生在分析法与综合法之间不断地灵活切换. 解决本题时,学生的真实思维经历了一个艰辛的探索历程,若思维缺乏一定的高度与宽度,则很难披荆斩棘,觅到突破口.
3. 教师忽视思维教学
课堂中,有些教师会以标准解题过程来掩盖探索结论的曲折过程. 教师所提供的标准解题过程,往往是基于教师本身认知水平上所呈现的思考与推理. 对于学生而言,因为认知水平的差异,导致思考问题的方式与起点不一样,最终对教师所呈现的标准解题过程只能说出“其然”,却无法理解“其所以然”.
面对教师直接呈现的标准解题过程,不少学生会提出这样的疑惑:“我为什么看不出这个结论?”“老师当时有没有遇到和我一样的障碍,当时他是怎么突破的?”“我的思路与老师不一样,是不是也有可行性?”这些都是需要教师思考面对的问题,只有基于“以生为本”的基础上进行的引导,才具有实际意义.
积极探索,培养推理能力
基于以上对于解题障碍成因的分析,笔者经过精心思考,设计了以下教学活动,与同行共勉!
1. 初步审题,找出有价值的信息
问题设计:根据本题所提供的条件信息,大家能获得哪些结论?解题需要应用到哪些条件?怎样才能充分发挥每个条件的最大作用?
设计意图 让学生带着问题去重新读题、审题,对题目所提供的条件进行全面分析,结合问题要求,提炼出可能需要用到的数学原理,为建构良好的解题思路铺路搭桥,而教师在此环节最重要的任务是关注学生审题后的实际反馈情况.
为了帮助学生理清如何提取有用信息的思路,可作如下引导:
问题1 观察图1,根据AB为☉O的直径这个条件,是否可从圆周角定理着手,推导出半圆所对的圆周角为直角的结论?
问题2 根据“BD为☉O的切线,交AC的延长于点D”这个条件,是否可结合圆的切线性质定理,联想到圆的切线与过切点的半径为互相垂直的关系?
问题3 结合“点C为圆弧AB的中点”,是否能联想到等弧所对的弦也是相等的?
问题4 根据“CE的延长线与切线BD相交于点F”这个条件,是否能联想到全等三角形相关知识?
问题5 根据“AF与☉O相交于点H,连结HB”这个条件,可否联想到直径或半圆所对的圆周角是直角?
问题6 根据“点E为BO的中点”这个条件,是否能找出特殊图形关系?
若学生在思考以上几个问题过程中,表现出对某个原理比较陌生的状态,就需要教师放慢教学节奏,与学生一起回顾相关原理,让学生从本源上理解这些结论的来龙去脉,为解题奠定基础. 同时,教师还要鼓励学生勇敢地表达出自己的所思所想,学生在尝试用数学语言表达的过程中,会不断地提取信息、整理思路、明晰知识结构.
当然,解决以上问题的过程,未必能全面地提取到每个条件所对应的所有价值,特别是根据“点E为BO的中点”这个条件找出相应的解题价值,确实存在一定难度. 因此,教师应从学生的角度去分析问题,从学生思维的卡壳点出发,引导学生通过观察、猜想、尝试、探索与证明等过程,寻找新的突破,学生因亲历整个结论的形成与发展过程,推理能力自然而然地能得到有效提升.
2. 紧扣目标,确定解题的突破口
问题设计:想要求出HB的长度,需要先求出哪些线段的长度?通过刚才的分析,有没有什么条件没有发挥其价值?
设计意图 引导学生根据自己原有的认知结构来探索未知,此问为学生的思维提供了明确的方向,让学生关注到关键图形间的联系.
学生对Rt△ABF中,双垂直的背景并不模式,也明白“知二求三”原理. 问题是题目只提供了AB的长,其他数据并不知晓,因此,如何求出BF的值是解开本题的关键.
有了明确的目标,学生再次回过头来思考“点E为BO的中点”这个条件的实际价值,将此条件与BF建立联系,可分离出一个重要的基本图形(见图2),这为后继辅助线的添加奠定了基础.
3. 验证猜想,促进推理能力发展
问题设计1:对于∠BAF=30°这个猜想是否可以验证?怎么验证?
设计意图 猜想出来的结论并不一定是正确的,验证是确定其是否合理的唯一方法. 此问的设计,目的是为了让学生对自己的猜想进行验证,以确定其是否合理.
学生面对此问,提出了以下两种验证方案:
方案1 直接用量角器测量,发现结论并不正确;
方案2 如图3,作图验证,具体方法为:分别以点A、F为圆心,BF的长度为半径作圆,所获得的两圆并非相切的关系,这与“在直角三角形中,30°角所对的直角边为斜边一半”的定理并不匹配,由此可确定这个猜想是错误的.
问题设计2:有没有办法找出和BF相等的线段?并证明.
设计意图 这为学生提供了观察猜想的目标,鼓励学生通过证明来对猜想进行论证,此时学生会将目光投入到图形中的等线段、对顶角等特殊条件中,为全等三角形的证明提供依据. 学生因经历了“方案制定→否定→新方案”的过程,逐渐深化了对问题的理解.
4. 画图分析,凸显图形依赖关系
问题设计:根据题目所提供的条件顺序,尝试画示意图,思考图中所呈现的线段长度是否确定,为什么?
设计意图 画图能让学生感知图形的确定性,从而思考图形关系对其确定性具有怎样的影响.
第一步:如图4,结合已知条件,设AB=2r,那么AC=BC=r;
第二步:如图5,根据条件“BD为☉O的切线,交AC的延长线于点D”,可知BD=2r;
第三步:如图6,根据点E为OB的中点这个条件求CE的长,可过点C作AB的垂线,连结OC后可以证得它与AB为垂直的关系,由此可得CE=r;
第四步:如图7,结合“CE的延长线与切线BD相交于点F”的条件,因为EB=OE=,tan∠BEF=tan∠CEO=2,所以BF=r,也可以根據△BEF?△OEC获得BF=CO=r.
第五步:如图8,根据“AF与☉O相交于点H,连结HB”的条件再结合以上结论,在Rt△ABF中,可用r表示AF、AH、BH、FH.
学生通过画图,对图形确定性进行定量分析,在作图活动过程中融入推理过程,其实就是逐步解三角形的过程. 尤其是第四步,对CE长进行确定与分析时,辅助线OC就自然生成,此时,全等的几何模型就自然形成了.
以上分析仅局限于对图象的确定性,不需要求出所有未知几何元素,我们只要根据解题需要求出相应的未知量即可. 比如在以上分析中,△COE是确定的,由此可得CE的长度,用三角函数来可得出BF的长度. 在△EBF中,结合∠BEF与BE的确定性,可以求出BF的长度. 这是典型的程序化思维模式,其实从全等的角度出发,可直接获得BF的值,这样就可以省掉一些计算.
5. 及时反思,积累解题经验
问题设计1:能否通过画图,获得解决这一类问题的一般程序?
设计意图 让学生通过画图,感知图形间的联系,对图形确定性形成深刻理解,感知数学转化思想方法在解题中的重要性,如通过对集中条件的思考,将问题转化成解三角形的问题.
几何问题本身就具有一定的开放性特征,若学生的思维随着条件无限发散出去,而不及时聚合,那么探索过程则缺乏明确的目的性,而影响解题效果[3]. 虽然对关于圆的综合题的分析,不像数与式那样具有显著的程序化特征,但也有一定的规律可循.
问题设计2:解题中,你们是如何突破思维的障碍点的?由此获得了什么启示?
设计意图 再还原思维的障碍点,可以让学生反思整个解题过程,从中发现自身思维的优缺点,积累良好的数学解题经验.
每个学生受各种综合因素的影响,知识储备有着较大差异,那么在思维障碍的成因上也各不相同,个性化的反思能让学生充分认识自身的不足. 从而进行有针对性的训练与调整,为掌握良好的解题技巧奠定基础.
总之,从本例题教学中,可以看出学生真实的认知水平与思维过程,这种教学模式使得整个课堂充满了“原生态”的味道,学生因亲历了整个探索与推理的过程,不仅有效地发展了自身的数学思维与推理能力,还促进了数学核心素养的形成与发展.
参考文献:
[1] 史宁中. 试论数学推理过程的逻辑性——兼论什么是有逻辑的推理[J].数学教育学报,2016,25(04):1-16,46.
[2] 中华人民共和国教育部. 义务教育数学课程标准(2011年版)[M]. 北京:北京师范大学出版社,2012.
[3] 拉尔夫·泰勒. 课程与教学的基本原理[M]. 施良方,译. 北京:人民教育出版社,1994.
