基于问题导学法应用的初中数学例题教学分析

徐黄娟

[摘  要] 问题导学法能有效激活学生的数学思维，提升学生的解题能力. 例题教学过程中，教师通过问题的精心设置，能有效启发学生的思维，锻炼学生的学习能力. 文章以一道题的教学为例，具体谈谈如何在初中数学课堂中，巧妙应用问题导学法激活学生的思维，发展学生的数学核心素养.

[关键词] 问题导学;课堂;思维

问题导学法是指在课堂教学过程中，教师结合教学内容提出一些问题供学生思考的一种教学方法. 学生在问题的引导下，通过自主探索、合作交流等方式对问题进行思考与分析，获得解决问题的能力，这对发展学生的数学综合素养具有重要促进作用.

问题导学中的“问题”，是指教师在课前精心设计的问题、课堂中随机产生的问题以及留给学生课后思考的问题等;“导”主要指教师适当的引导，即在“问题”的基础上，引导学生进入积极的思考与学习状态;“学”为学生的学习，包含学生的思维、学习效率与能力等综合因素[1].

问题导学法的优势

随着新课改这股风的刮起，萌生出众多教学方法，问题导学法在众多新兴的方法中脱颖而出，它既存在独有的优势，又能与其他教学方法互通、交融，受到广大教育工作者的青睐.

1. 激发兴趣，启发思维

初中数学与小学数学相比，更显枯燥、乏味，不少学生将精力放在对公式、定理等的记忆上，使得学习积极性不够，课堂活跃度差，长此以往，必然会对学生的学习兴趣产生消极影响. 问题导学以“问题”为起点，引导学生围绕问题进行探索分析，并结合合作学习法的应用，不仅能快速调动学生的积极性，营造出和谐、舒适的课堂氛围，还能有效地启发学生的数学思维，强化学生对知识的理解程度.

2. 以生为本，教学相长

新课标一再强调学生才是课堂的主人. 问题导学法主张学生在课堂中的主体性地位，坚持在“以生为本”的原则下开展教学活动. 虽然这种教学方法与传统“注入式”的教学模式相比，需要教育工作者花费更多的时间与精力去挖掘教材、了解学生、研究问题的设计等，但所取得的教学成效是传统教学模式无法比拟的. 问题导学法不仅可以提升教师的教学能力，激发学生的主人翁意识，还能从很大程度上改善学生课堂活动参与的积极性，从真正意义上实现教学相长.

3. 巩固知识，提升能力

问题导学固然是以提问为教学的主要模式，而问题又是結合学生实际情况而产生的. 教师设计问题时，常会综合考虑学生的知识掌握程度来明确问题方向与难度，设计出的每一个问题都具有明确的针对性与挑战性，以达到帮助学生巩固知识的作用. 学生针对问题进行思考、探索与分析的过程，不仅是解决问题的过程，还是形成良好猜想、推理、归纳总结等能力的过程[2].

问题导学法的应用分析

笔者在一次听课中，偶得一则以问题为主导的例题教学案例，恰与近期所研究的“问题导学法的应用”相契合，故做如下整理，谈一些拙见.

原题：用一根10米长的铁丝围一个长方形.

问题：（1）围成的长方形，宽比长短1.4米，求长方形的长与宽;

（2）围成的长方形，长比宽多0.8米，求长方形的长与宽;

（3）若围成一个正方形，边长为多少？正方形的面积与问题（2）所围成的长方形的面积相比，有什么变化？

1. 教学简录

师：从“将一根10米长的铁丝围成一个长方形”这句话中，我们能不能求出长方形的长与宽？为什么？

生1：从这个条件出发，我们只能得出所围成的长方形具备“长+宽=5（米）”这个条件，无法求出长与宽的具体值.

师：通过简短的一句话，你们能抓住“长+宽=5（米）”这个条件，非常好！除此之外，还能从其他角度进行分析吗？

生2：假设所围成的长方形的长为x米，则宽为（5-x）米，从“长+宽=5（米）”这个条件出发，列式为x+（5-x）=5，经计算发现x消失了.

师：思路看似没问题，但通过一个相等关系设未知数并列方程，固然会出现循环现象，无法达到预期效果.

生3：在已知“长+宽=5（米）”这个条件后，只要知道长或宽任意一个值，就能得到一个与之相对应的结论. 若长为4米，则宽必然为1米;若长为3米，则宽必然为2米.

师：从你的表述中，我看到了从一般到特殊的数学思想. 同时，还提到了“对应”这个词语，非常好！

生4：从以上分析来看，铁丝所围成的长方形存在这样一个规律：长变大，则宽变小;长变小，则宽变大. 不论两者怎么改变，长与宽的和不会发生变化. 由此也能看出，若不指定长与宽，则可围成无数种长方形.

师：很好，这是从运动变化的角度来看待这个问题的，思路非常清晰，值得赞扬！通过以上讨论不难发现，只知道周长，无法确定长方形的形状，想要围成固定的长方形，需要知道什么条件？

生5：必然要知道长或宽其中一个条件，比如长为3.5米，求宽的值.

生6：好直白，感觉像小学生做的题目，毫无挑战性.

师：生5的说法虽然简单，但也有一定的意义. 这种表述其实就是之前我们遇到的“代数式求值问题”，但是探究空间与价值不是很大.

生7：或许在长与宽之间加上另一种数量关系，会有新的收获.

师：哦？这个想法挺有意思，现在请大家发挥自己的想象为长与宽匹配一种恰当的数量关系.

学生针对此问进行分类、探索，获得了以下三种结论：①增减关系，如长比宽多0.5米，宽比长少1.5米等;②倍数关系，如长 ∶ 宽=2 ∶ 1，宽为长的，长为宽的3倍等;③以上两种关系的混合，如长比宽的3倍多0.5米，宽比长的2倍少0.5米等.

根据学生自主获得的三种结论，教师从中挑选出了以下三个具有代表性的问题：①将10米长的铁丝围成一个长比宽多0.8米的长方形，求该长方形的长与宽;②将10米长的铁丝围成一个“长 ∶ 宽为2 ∶ 1”的长方形，求该长方形的长与宽;③将10米长的铁丝围成一个长比宽的2倍少1米的长方形，求该长方形的长与宽.

针对问题①，学生给出了以下两种解法：

解法1：设所围成的长方形的宽是x米，则长为（x+0.8）米，结合题意，列式x+（x+0.8）=10×，解得宽x=2.1（米），则长为2.1+0.8=2.9（米）.

解法2：设所围成的长方形的长为x米，则宽为（5-x）米，结合题意，列式（5-x）+0.8=x，解得长x=2.9（米），则宽为5-2.9=2.1（米）.

针对问题②，学生给出了以下三种解法：

解法1：长=5×=（米），宽=5×=（米）.

解法2：假设所围成的长方形的宽为x米，则长为2x米，结合题意，列式2x+x=10×，解得宽x=（米），则长为2×=（米）.

解法3：假设所围成的长方形的长为x米，则宽为（5-x）米，结合题意，列式2（5-x）=x，解得长x=（米），则宽为5-x=5-=（米）.

针对问题③，学生给出了以下两种解法：

解法1：假设所围成的长方形的宽是x米，则长为（2x-1）米，结合题意，列式x+（2x-1）=10×，解得宽x=2（米），则长为2x-1=3米.

解法2：假设所围成的长方形的长是x米，则宽为（5-x）米，结合题意，列式2（5-x）-1=x，解得长x=3（米），则宽为5-x=2（米）.

师：观察发现，大家的计算过程分别应用了算术法与方程法，在应用中你们有什么体验？

生8：用算术法比较繁杂，方程法更加简便.

师：列方程的关键是什么？

生9：必须准确地找出问题中存在的等量关系.

师：非常好！从以上解题过程来看，大家都能根据问题找到其中所蕴含的等量关系，并用算术法与方程法解决问题. 今后遇到一些复杂的问题，可从方程的角度出发，化繁为简，提高解题效率. 在铁丝的总长不发生变化的情况下，所围成的不同长方形的面积有没有变化？说明理由.

（学生在独立思考的基础上开展合作学习）

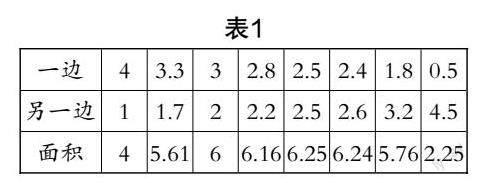
组1：我们组经过探索发现，同一根铁丝所围成的不同长方形的面积不一样，其中存在一定的规律，即当长与宽的数值越接近时，所获得的长方形的面积越大. 其实这个规律大家都知道，咱们组讨论的主题是怎么说明此规律，若提取几组数据进行分析，只能获得猜想，并不能说明问题. 因此，我们选择列表（见表1）的方式，将数据呈现出来，便于观察分析.

师：不错！你们借助表格将数据整理出来，其中的关系一目了然. 这种直观、简洁的思考方式非常可取，值得借鉴.

组2：我们组还有更加简便、直观的方法呢！我们想要知道边长变化时，长方形的面积是怎么变化的，统计图则能直观地反映出其中的變化规律. 如表2，我们先将数据整理在表格中.

如图1所示，将长方形的面积在方格纸上进行标注，找出这些点的分布规律，从点的走势可以直观地看到所围成的长方形的最大面积为6.25，即边长为2.5的正方形，这与我们原有的认知一致.

师：非常好！这种方法所呈现的视觉效果更加明显，从图中我们能一眼看出长方形两边边长变化与面积的关系，其他组还有不同的见解吗？

组3：总感觉数据太多了，而且我们也不可能将每一个数据都取到，那么所得到的结论就含有猜想成分，并不符合数学的严谨性特征，我们组在思考有没有更具说服力的方法.

师：这个想法不错，前两组的结论都是根据“长+宽=5（米）”这个条件提取的特殊值，并借助表格和描点的方法寻找其中所蕴含的规律，此为典型的从一般到特殊的数学思想方法. 现在第三组提出要寻找一种更加合适的方法来表达规律的成立，此为从特殊到一般的方法. 将几个小组的方法综合在一起，则为探索数学事物一般规律的基本策略. 此问确实存在更加方便，且更具一般性的解决方法，这个知识将在后期二次函数的学习中与大家碰面.

至此，教师带领学生回归到原题，学生很快就自主解决了所有问题.

2. 教学分析

观察以上教学实录，主要呈现出以下几个问题：①将一根10米长的铁丝围成一个长方形，是否可以知道它的长与宽？为什么？②有什么办法让所围成的长方形有确定的长与宽？③将10米长的铁丝围出的长方形，宽比长少0.8米，求长与宽分别是多少. ④所围成的长方形，长与宽的比为2 ∶ 1，求长方形的长与宽;⑤所围成的长方形的长比宽的2倍少1米，求长与宽分别是多少. ⑥为什么大部分问题选择方程来解决？⑦用方程解决数学问题的关键是什么？⑧所围成的长方形的面积与长、宽之间有什么联系？说明理由. ⑨寻找一种更具说服力的方法，来探寻长方形的面积与长、宽之间所存在的规律.

纵观这些问题，会发现第一个问题属于原生态问题，它来自生活实际，蕴含着丰富的数学思维. 这个问题的起点低，却有很强的延伸性，初始问题为学生的思维提供了较大的思考空间，也为学生提供了深入探索的机会. 因此，第一个问题可以理解为本节课问题导学的灵魂，是接下来所有问题的引擎.

问题①③⑥⑦⑧均由教师提出，问题②④⑤⑨则由课堂自动生成. 其中，问题①③⑥⑧属于发散性问题，同时只有⑥为一个聚合性问题. 由此可见，本节课的问题导学，主要针对建立方程模型而设计，以渗透数学思想方法为目标，意在培养学生发现问题、提出问题与解决问题的能力.

问题①③的提出，有效地调动了学生的探究热情，让学生将精力投入问题的探究中去，促进分析与推理能力的形成与发展，为其他问题的提出与生成奠定了良好的基础. 前7个问题都是围绕“长+宽=5（米）”这个等量关系提出的，让学生明确用方程解决问题的关键在于寻找等量关系.

问题⑧作为一个探究活动，让学生在独立思考的基础上进行小组合作学习，不仅训练学生计算、观察、推理与总结的能力，还有效地推动学生数据分析、归纳推理等数学核心素养的形成与发展. 因为有了问题⑧的探究性活动作为基础，使得问题⑨应运而生，为后期二次函数的学习做好铺垫.

教师在处理这9个问题的过程中，引导学生独立思考、自主探究与合作学习，不仅仅有效地活跃了学生的思维，更重要的是让学生积累了自主解决问题的经验，获得了良好的学习体验，增进了学习的主人翁意识与团队精神. 问题导学的过程中，师生、生生在积极的互动与交流中，有效地促进了逻辑推理、直观想象、数据分析等能力的发展，为数学核心素养的提升奠定了坚实的基础.

总之，问题导学法是新课改背景下，数学课堂创新理念的体现，是提高教学效率与质量的基本措施. 实际教学过程中，可能会涌现出层出不穷的问题，作为一线的数学教师，应做到与时俱进，结合实际情况设计出新颖、合理的问题.

参考文献：

[1]郑毓信. “问题意识”与数学教师的专业成长[J].数学教育学报，2017，26（05）：1-5，92.

[2]G·波利亚. 数学与猜想数学中的归纳与类比[M]. 李心灿，王日爽，李志尧，译. 北京：科学出版社，2001.