数学问题设计的误区和出路

摘要：数学问题可以分为回忆型、连接型、反省型三类。一味重视练习题（回忆型问题），使得过程思维的发展空间狭窄。开放题（反省型问题）的出现，旨在平衡内容知识与过程思维。但是，开放题在进入日常教学时，遭遇了一些障碍。对此，应该重视连接型问题组的设计，将其作为课程载体，促进从基础知识到高层次思维的连续发展，促进内容与过程的平衡。

关键词：数学问题；练习题；开放题；连接型问题组

近几十年来，美国数学课程中，“问题解决”被调整为数学教育的过程目标之一，而不再像以前一样作为数学教育的“核心”。这与“问题解决”中将问题界定为不熟悉的问题有关：把不熟悉的问题绝对化，违背循序渐进的原则，因为，从熟悉的问题到不熟悉的问题需要过渡和连接；忽视人类学习的一般规律，毕竟，从熟悉的问题到不熟悉的问题的迁移学习扮演着重要的角色。此外，许多研究单单关注问题提出或思维，脱离知识。这样的“问题解决”犹如离开水的鱼，难以长期發展。

一、数学问题的分类和角色

问题在数学课程中扮演非常重要的角色。简单来说，简单问题（通常意义上的练习）和例题类似，扮演记忆例题方法的角色，某种意义上，可以作为“双基”的课程桥梁；难的问题需要思考探索，扮演思维的角色，某种意义上，可以作为高层次思维能力的课程载体。

PISA曾按照一个公民在日常生活中理解数学、作出判断、使用和从事数学的能力评价学习者的数学素养，把用于评价的数学问题更为清晰地分为回忆型（reproduce cluster）问题、连接型（connection cluster）问题、反省型（reflection cluster）问题三类，较为广泛地被公众所接受。

回忆型问题是指涉及回忆练习性的知识，关联标准算法、技巧，标准公式、应用计算，常规性操作、常规问题解决的问题。其特征包括标准表征和定义、常规问题解决。例如：（1）（PISA 2003第7号例子）把69％写成分数。（2）（PISA 2003第6号例子）求7、12、8、14、15、9的平均数。

连接型问题是指在回忆型问题的基础上，在熟悉或半熟悉的背景下，涉及并不简单的常规问题解决，需要把不同的问题表征进行整合，连接不同的课程内容的问题。其特征包括模型化、标准问题解决的转化与整合、多种常规结构方法的整合。例如：（1）（PISA2003第10号例子）马丽距离学校2公里，马丁距离学校5公里，他们距离有多远？（2）（PISA 2003第12号例子）一个比萨公司生产两种同样厚度的比萨，小的直径30cm，卖30zeds，大的直径40cm，卖40 zeds，哪种更值？解释你的推理。

反省型问题是指在连接型问题的基础上，解决过程更有创造性或更加陌生，涉及高级推理、抽象化、概括性、应用新背景模型化能力的问题。其特征包括复杂的问题解决和提出、反省和深度洞察、创造性的方法、多种复杂方法等。例如：（PISA 2003第14号例子）某个国家1980年的国防开支是3千万美元，当年的国民收入总值是50千万美元；1981年的国防开支是3.5千万美元，当年的国民收入总值是60.5千万美元。两年来国民收入总值的通货膨胀率为10％。如果你被邀请为和平爱好者做演说，你打算解释国防开支降低，你如何来做？如果你被邀请为军事学术部门做演说，你打算解释国防开支提高，你如何来做？

这三类问题，搭建起了“容易一中难一最难”的阶梯。其中，回忆型问题可以用来学习内容知识；反省型问题可以用来学习过程思维；连接型问题是对内容知识和过程思维的统整，也可说是对内容知识的消化吸收，在不同的情境下灵活应用，是进一步解决更开放的反省型问题，学习过程思维，形成高层次思维能力的中间过渡载体。

二、开放题的出现，旨在平衡内容与过程

事实上，问题设计常常出现两个极端，或者重视回忆型问题，或者强调反省型问题，而相对地忽视中间过渡的连接型问题。这导致缺乏内容知识与过程思维的平衡。正如黄毅英等人所强调的，各国数学课程改革亟待解决的问题就是内容与过程的平衡：“各国数学课程改革的新趋势表明，于响应社会转型的挑战中，培育下一代之高层次思维能力至为重要。但如何同时保持坚定的基础知识，是当前数学课程发展刻不容缓的任务。如何在提升高层次思维能力和共通能力之余不会丢失坚实的学科基础，以及如何在'过程'与'内容'间找到平衡，变成众多问题的重中之重。”

重视内容的教学问题扮演了知识掌握的角色，主要以一般性的练习题（回忆型问题）为载体，以课堂例题、课堂练习、课后练习等形式呈现，帮助学生巩固和发展概念、法则、定理等。一般性练习题的完整条件，使学生只要回忆学过的知识，选择合适的知识，即可作出回答，即“只要记，不用想”。而这就意味着过程思维（尤其是高层次思维）的发展空间狭窄。

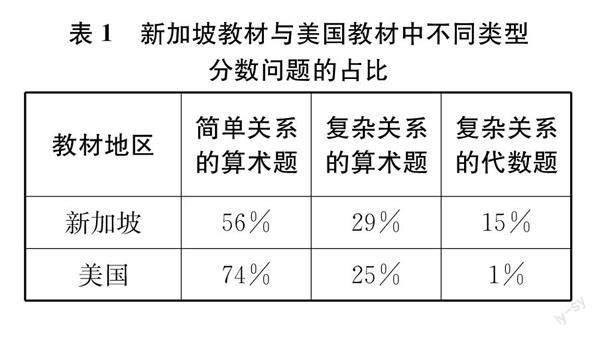
以美国为例。部分美国教材编写者为提升学生学习数学的兴趣，也为使每一个学生都能解决教材提供的问题，让每一单元的问题都倾向解决一般形式的简单模式。[2]有学者统计过一本新加坡教材和一本美国教材中不同类型分数问题的占比，结果如表1所示。显然，美国教材中的问题更浅、更易。

在一定程度上，开放题被视为解决上述问题的对策—这也是开放题受到重视的原因之一。

1971年，岛田茂等人编著的《开放式途径：关于数学教学的一个新建议》出版，正式提出了开放题。后来，各个国家的研究者把它贴上了不同的标签，比如现实主义数学（realistic mathematics）、调查性项目（investigative project）、探索性问题（exploratory problem）、真实的数学调查与问题提出（authentic mathematical investigation and problem posing）、开放式方法（open- ended approach）、结构不良问题（ill-structure problem）、开放式问题（open problem）。尽管不同的标签代表不同的研究倾向、意义趋向，但是它们的基本含义是相同的。开放题在近几十年全世界的数学教育领域备受瞩目，其深层次原因在于：弥补了一般性练习所缺乏的，为发展数学过程思维（尤其高层次思维）提供的自由空间（课程载体），使数学学习相对于一般性的练习具备了更为深层（从任务到结果）的“过程”循环。

简单地说，开放题通过开放研究的任务和目标，开放条件或结论，即控制条件和结论的自由度，扩大题设空间，促使解题者扩大探索试验空间，产生多种策略。也就是说，开放题让解题者有更多情感充分投入，有更多机会建构自己的方法，驱动相对高层次的数学思维，输出相对深层结构的学习结果，对数学的本质和价值有相对深层的体会。

以此为线索，人们进一步发现，若只有回忆型练习，则收窄了学习的任务和目标，容易导致解题者情感与策略的浅层参与，使用机械的、记忆题型的浅层数学学习方式，获得学习结果的浅层结构。而浅层认知结构，传递歪曲的数学态度和观念、浅层的数学本质和价值体会，易使数学学习变为由起点到终点的“浅循环”。

三、开放题在进入日常教学时，遭遇了障碍

重视培养过程思维的课程主要以开放题（反省型问题）为载体。虽然开放题为高层次思维提供了可能，但它在进入日常教學时，遭遇了一些障碍。

首先，开放题对教师教学要求较高。一方面，解决开放题需要高层次思维。换句话说，开放题能为学生的思维发展提供较为广阔的空间。这是开放题受到重视的主要原因。另一方面，既然解决开放题需要高层次思维，那么，学生不会时，教师该如何来教？这对教师提出了较高的要求。开放题教学如何进一步在中小学推广和普及是当务之急，高层次思维不是空中楼阁，也不会自动生成，仍需要教学和课程的支持。[4]

其次，开放题让学生学习信心受挫。黄毅英等人研究发现，大部分学生面对开放题时有失控感、挫败感。几次解不出来，学习数学的成就感、自信心也会降低，并由此不喜欢开放题—甚至能力较强的学生也不喜欢。的确，渴望成功是学生发展的第一需要，成就感是学生学习动机之基础。也有学者提及开放题教学遇到的障碍如下：（1）开放题在单一的技能训练、知识学习上费时费力，效率较低；（2）开放题教学容易受到课时的限制，课堂上常出现学生的思维在低层次上重复、不易进入深度研究的情况；（3）现有适合教学的开放题数量太少，而开发和设计更多的开放题面临较多的困难；（4）对有些开放题很难制定出客观、公正的标准，故用开放题做考试题困难重重。[6]

再次，开放题让师生不习惯。长期以来，师生已经习惯练习题，视开放题为“额外的负担”“多余的任务”。如此，课程的研究者对开放题的推行在不被接受的情况下，就变为“一厢情愿”，面临巨大挑战。

最后，开放题和日常教学脱离。开放题教学一直是“缺米之炊”“缺源之水”。开放题的设计非常困难，主要表现为教师很难准备背景，以及题目很难合适学生的水平，很难结合学生的知识。”例如，关于开放题的代表性著作《开放式途径：关于数学教学的一个新建议》中所提出的，后来被视为典型开放题的棒球游戏和石子问题（baseball games，marble problem）适合任何年级的学生。这便从另一个侧面说明，题目没有结合学生的知识，并和日常教学脱离。当前的开放题教学在一定意义上只是日常数学教学的补充（常被形象地描述为“主食外的甜品”）。例如，戴再平提出的典型的开放题—邮路问题，虽然数学意义深刻，但只能成为日常数学教学的补充，对学生数学学习的影响不大。由此看来，离开传统的数学教学内容，与日常数学教学分家，开放题只能成为短暂的开阔思维、类似“脑筋急转弯”的数学游戏，很难在数学课堂长久扎根，其教育价值很难真正落实。

香港的情况更说明了这一点。2001年，香港教育署为了协助教师在中学一年级推行《中学课程纲要：数学科（中一至中五）》，提供了较为详尽的帮助学生发展高层次思维的题目。例如：“大文正在筹备一个茶会。他买了一些饮品和鸡翅。饮品每包5元，鸡翅每只8元。（1）现有8人（包括大文）参加茶会。每人有1包饮品及2只鸡翅。问大文需为茶会付款多少？（2）现有9人（包括大文）参加茶会。每人有3包饮品和一些鸡翅。大文共付423元。问每人有多少只鸡翅？（3）现有n人（包括大文）参加茶会。每人有x包饮品及2x只鸡翅。大文共付款273元。参加茶会的人数是多少？每人有多少包饮品及多少只鸡翅？”另搞一套教学资源，不言而喻，说明高层次思维培养和日常教学是脱离的。

四、连接型问题组应运而生

从根本上说，开放题遭遇这些障碍，是因为将它与练习题截然分开，而忽视了它们通过连接型问题连接起来的可能性与必要性。因此，克服上述障碍的出路便在于，重视通过连接型问题连接回忆型问题和反省型问题的问题组（可以把这样的问题组称为“连接型问题组”）的设计，从而将其作为课程载体，促进从基础的知识到高层次思维的连续发展，促进内容与过程的平衡。

除了从包含的问题类型看，还可以从变化（变式）的角度看连接型问题组，即与例题相比，存在“小一中一大”的连续变化（“容易一中难一最难”的层次难度）。由此，在广义上，连接型问题组是一种变式题组，也可以只包含回忆型问题与连接型问题。

下面，先来看连接型问题组存在的可能性。理论上，根据上述PISA的问题分类框架，从回忆型问题到反省型问题存在连接的可能性。实际上，在中国内地的数学课程中，有很多连接型问题组，其背后有深层次的文化土壤和根源。[9]这里，我们仅给出一个根据上述PISA 2003第14号例子设计的连接型问题组。

PISA 2003第14号例子是一个评价高层次思维的反省型问题。据此，可以设计如下回忆型问题和连接型问题，组成连接型问题组，从而实现从内容知识到过程思维的逐级提升。

【回忆型问题】

某个国家1980年的国防开支是3千万美元，当年的国民收入总值50千万美元；1981年的国防开支是3.5千万美元，当年的国民收入总值60.5千万美元。两年来国民收入总值的通货膨胀率为10％。1981年比1980年的国防开支多多少千万美元？（或1980年比1981年的国防开支少多少千万美元？）1980年的国防开支占国民收入总值的百分比是多少？1981年的国防开支占国民收入总值的百分比是多少？

【连接型问题】

某个国家1980年的国防开支是3千万美元，当年的国民收入总值50千万美元；1981年的国防开支是3.5千万美元，当年的国民收入总值60.5千万美元。两年来国民收入总值的通货膨胀率为10％。1981年的国防开支比1980年的国防开支多还是少？多多少？少多少？扣除通货膨胀呢？说说你如何得出你的结论。

再来看连接型问题组存在的必要性：相比于单道题，更强调问题之间的关系，更强调深层的数学意义与结构理解，更能够促进学习的循序渐进、螺旋上升。下面简单举几个例子：

【连接型问题组1】

（1）6个饼，2个饼分一碟，共分多少碟？（2）6个饼，共分3碟，每碟有多少个饼？（3）要多少个饼，才可以2个饼分一碟，共分3碟？

这里，第一题，学生记住除法的意义，就可以解答；第二题，学生必须比较其与第一题的异同，理解“包含除”与“等分除”的异同；第三题，学生必须思考除法的本质特征是什么，除法和乘法的联系是什么。因此，这个连接型问题组通过变化的连续性，连接除法的内容知识和过程思维，促进学习的循序渐进。

另外，这个连接型问题组相比于第一题这样的单道题，优势在于更强调除法和乘法的关系（学生不容易区分的元素），更强调“恒等”的数学结构，更强调“方程”的数学思想，而不是除法的简单应用。

【连接型问题组2】

（1）3包巧克力，6个人分，每人分多少包？

（2）6包巧克力，3个人分，每人分多少包？

这个连接型问题组不仅聚焦除法的应用，而且区分了被除数和除数的位置关系—不是由大小决定的，并非被除数总是大于除数。

【连接型问题组3】

（1）妈妈买了6个饼，小明分得2个饼，小明得到几分之几？

（2）妈妈买了6个饼，小明分得，小明得到几个饼？

（3）小明分得2个饼，占总数的，妈妈买了几个饼？

（4）妈妈买了6个饼，小明分得1／3个，还剩几个饼？

这个连接型问题组突出了分数乘法、除法和分数概念之间的联系和区别，区分了分数的比率意义和数量意义（无单位和有单位）。这些都是学生通常难以区分，造成分数意义与运算理解困难的元素。

五、结语

概括而言，使用练习题引领学生开展知识学习，使用开放题指导学生进行问题解决，这种分离带来了极端的问题：学科知识在问题解决中趋于无用；而且，问题解决的发展也不足以支持学科知识的发展。

同时，一些研究指出，问题解决使数学知识学习“碎片化”。有研究认为，情境在问题解决中的作用被过分强调了，而知识（经验）被过分忽视了；情境学习的核心主张，比如行动基于其发生的具体情境，知识不会在任务之间迁移，抽象思维的用处不大，教学必须在复杂的社会环境中进行……则过分夸大了情境教育的意义。”实际上，数学知识有助于解释情境的先决条件，数学知识和思维策略必须同时学习和使用。而从结构良好的问题到结构不良的问题应该是连续的，不是绝对二分的—例如，背诵“九九表”可以改为在“九九表”中查找多重关系。

特别要提的是，通过问题变式形成的连056接型问题组，在数学教学中发挥着重要的作用。然而，很多教师不知道“连接型问题组”这一提法，而较为通俗地称之为分散难点问题、题组或问题串、问题链。这导致相对于其重要性而言，连接型问题组在问题解决领域缺乏系统深入的研究—这实际上是一种“捧着金饭碗要饭”（郑毓信教授语）的现象。笔者希望本文能起到抛砖引玉的作用，引起大家对连接型问题组的进一步重视和研究。参考文献：

[1]黄毅英，林智中，孫旭花．变式教学课程设计原理：数学课程改革的可能出路[M].香港：香港教育研究所，2006：5．

[2]W.Schmidt，R.Houang，L.Cogan.A coherent curriculum[J].American Education， 2002（10）：1-18.

[3]B.H.Yeap，B.J.Ferrucci， J.A. Carter.A comparative study of arithmetic problems in Singapore and American textbooks[C]// F.K.S. Leung，K.Graf，F.Lopez-Real.Study Volume of ICMI 13th Study on Comparative Studies Netherlands：Kluwer Academic publishers，2006：1.

[4][6]龚雷．数学开放题的概念及其分类[M]／／戴再平.开放题：数学教学的新模式.上海：上海教育出版社，2002：50—60，50—60．

[5]N.Y.Wong，M.M. Chiu，K.M. Wong， et al. The lived space of mathematics learning： An attempt for change [J].Research in Mathema-tical Education，2005（1）：25-45. [7]J.Becker，S Shimada. The open-ended approach：A new proposal for teaching mathematics [M].Reston，VA：National Council of teachers of Mathematics，1997：43-57.

[8]香港教育署数学组．开放题教学资源套[M]．香港：政府印务处，2001：13．

[9]X.H.Sun，N.Y.Wong，C.C.Lam. Bianshi problem as the bridge from “entering the way” to “transcendng the way"：the cultural characteristic of Bianshi problem in Chinese math education [J].Journal of the Korean Society Mathematical Education Series： Research in Mathematical Education，2005（2）：153-172. [10] J. R. Anderson，L. M. Reder，H.A. Simon. Situated learning and education [J]. Educational researcher，1996（4）：5-11.

（孙旭花，澳门大学教育学院，助理教授。在广州、香港、澳门等地负责中小学数学教师培训30多年。曾担任国际数学教育委员会“整数的数学教与学”专题国际统筹研究委员会协同主席、数学史与数学教育的关系国际研究小组协同主席，并于第13界国际数学教育大会做邀请报告。在中外期刊发表论文100余篇，主编斯普林格英文畅销书《打好基础：整数教学》，著有《螺旋变式—解读中国内地数学课程与教学之逻辑》。）