例说全概率公式与贝叶斯公式的运用

广东省惠州市第一中学 (516007) 方志平

全概率公式在新版高中数学教材中具备“承上启下”的过渡作用,是条件概率概念的延伸,应用的关键是对样本空间做好划分,在表现形式上拓展了条件概率,同时也作为贝叶斯公式成立的理论基础．贝叶斯公式是概率论中极为重要的公式,它以其灵活的特性与简洁的表达方式,受到了广泛重视.贝叶斯公式的意义在于,根据事件的结果可以探寻引起该事件发生的原因,即“执果求因”.下面举例说明全概率公式与贝叶斯公式的实际运用,供教与学参考.

1．全概率公式与贝叶斯公式的介绍

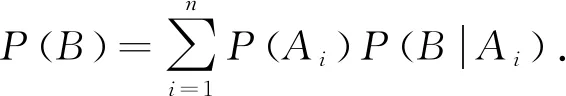
注意：①在对样本空间Ω的划分时,一定要把导致事件B(称为目标事件)发生的所有可能性A1,A2,…,An全找出来,并保证A1,A2,…,An为两两互不相容的事件,做到“不重不漏”.在此基础上,全概率公式的实质就是通过样本空间的一个合适的划分,将一个复杂事件的概率转化为若干个简单事件的概率之和,使复杂问题简单化.这正是数学中常用的“化整为零”的思想.

②如果把A1,A2,…,An看作是引起事件B发生的所有可能“原因”,那么全概率公式表明,目标事件B发生的概率实际上就是该事件在这些“原因”下的条件概率的加权平均,其中权重分别为P(Ai).因此,全概率公式也称为“由因导果”公式.

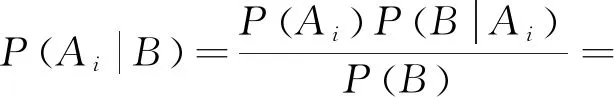
注意：贝叶斯公式不同于全概率公式的是两个的侧重点不同.贝叶斯公式主要作用是在事故产生后,对于事故责任的划分,体现出的是一种“问责”,即“执果求因”.

2．全概率公式与贝叶斯公式的运用

概率是反映随机事件出现的可能性大小的度量,而条件概率则是在给定某事件A的条件下,另一事件B发生的概率,事件A与事件B的关系会影响条件概率.全概率公式则是利用条件概率,将复杂的事件B分割为若干简单事件概率的求和问题,而贝叶斯公式则是利用条件概率和全概率公式计算后验概率.

例1 有两只箱子,每只都有6个白球4个红球,现从第一只箱中任取一球放入第二只箱,再从第二只箱中任取一球,求取到红球的概率.

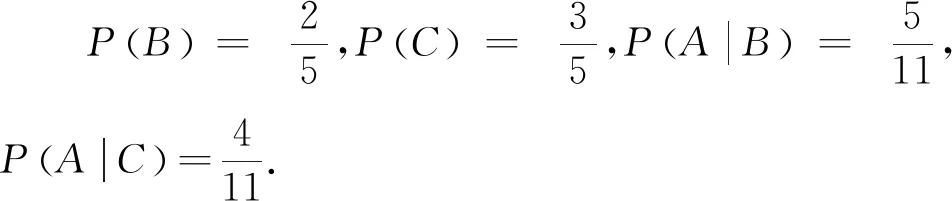
评注：由上述解法可以看出,应用的关键就是“执果索因”,即先找到事件A发生的原因,在寻找原因的时候,要把原因拆分成为互斥的事件B与C,掌握了这个原理,对全概率公式的理解就会有更深一步的认识,而不是仅仅停留在记忆公式的层面.

例2 两箱产品,第一个箱子里面装有10个合格品和40个次品,第二个箱子里面装有18个合格品和12个次品,随机挑中两个箱子中的一个并随机拿出两个产品,如果第一次拿出的是合格产品,问抽到的是第一箱的概率为多少?

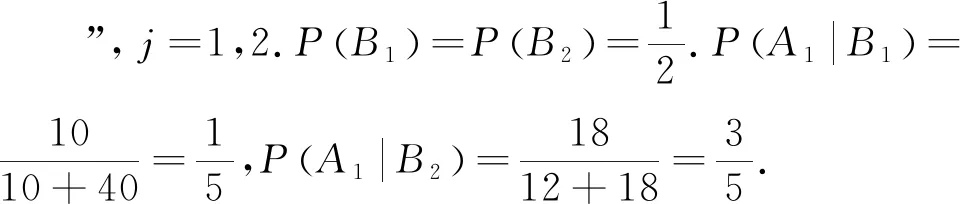
评注：本题的难点是将实际问题转化为数学模型,需要我们读懂题意,合理设出事件,用数学符号准确表示事件.要弄清第一次拿到的东西是合格品,可能是来自第一箱,也可能是来自第二箱,利用全概率公式求出P(A1).再用贝叶斯公式求出第一次拿出的是合格产品,是来自第一箱的概率P(B1|A1).

例3 某玩具制造厂所用的遥控飞机零件,是由5家不同的玩具零件制造厂提供的,我们根据以往的数据分析得以下数据:一厂的零件次品率为0.01,二厂的零件次品率为0.02,三厂的零件次品率为0.02,四厂的零件次品率为0.01,五厂的零件次品率为0.03.而它们所提供的零件份额:一厂的份额是0.2,二厂的份额是0.2,三厂的份额是0.3,四厂的份额是0.2,五厂的份额是0.1.已知在玩具厂的零件储藏室里,由这四家玩具零件制造厂提供的飞机零件的离合器,是均匀的混在一起放置的,而且在外观上看没有任何区别.

(1)随机在储藏室里取一个离合器,求此离合器为次品的概率;

(2)随机在储藏室里取一个离合器,若取到的离合器是一件次品,请分析此次品出自何厂的几率最大?

解：(1)设事件A=“取到的是次品”,事件B=“取到的产品是第i家玩具零件制造厂提供的”(i=1,2,3,4,5),则P(B1)=0.2,P(B,2)=0.2,P(B3)=0.3,P(B4)=0.2,P(B5)=0.1.P(A|B1)

=0.01,P(A|B2)=0.02,P(A|B3)=0.02,P(A|B4)=0.01,P(A|B5)=0.03.

(2)由贝叶斯公式得

故(1)随机在储藏室里取一个离合器,此离合器为次品的概率为0.017;(2)这个次品出自三厂的可能性最大.

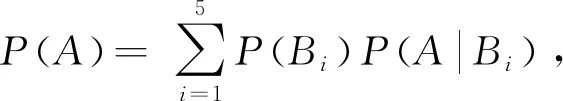
例4 假定小明去参加数学夏令营,选择乘火车、轮船、汽车、飞机的概率分别为0.3,0.2,0.1,0.4,若他乘火车、轮船、汽车迟到的概率分别为0.2,0.3和0.5,而乘飞机则不会迟到.结果他迟到了,那么他是乘火车去参加数学夏令营的概率是多少?

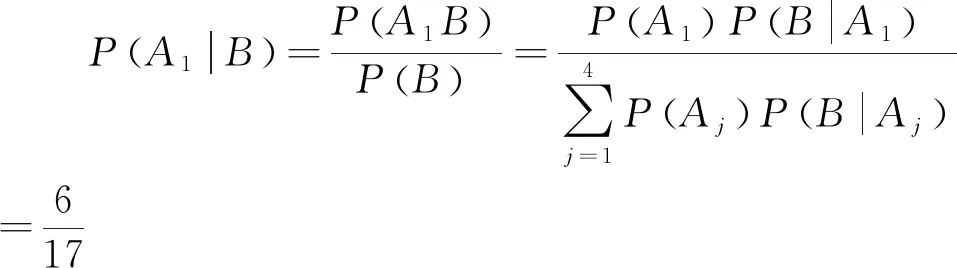
评注：本题实质上是利用全概率公式,先求小明迟到的概率P(B),在迟到的前提下由贝叶斯公式求小明因迟到而乘火车参加夏令营的概率P(A1|B).

例5 某厂有一、二、三共三个车间,生产同种产品,总产量中三个车间所占的比例分别是60%、25%及15%,三个车间所生产产品的次品率分别为6%、8%及12%,从该厂产品中任意抽取一件产品,取到的恰好是次品,视次品来自一或二或三车间,能被修复成正品的概率分别为0.8,0.5,0.3,求此次品能被修复成正品的概率是多少?

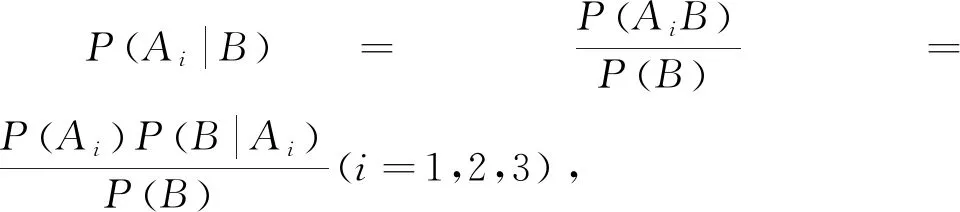
评注：首先要理解来自第i车间的次品被修复成正品的概率是P(C|AiB)(i=1,2,3),其次要结合贝叶斯公式及概率的加权平均,方可求出结果.

综上,全概率公式包含了事件的并与互不相容的概念,还包括着加法、乘法公式,条件概率公式,而贝叶斯公式则是根据全概率公式推导演化而来的．全概率公式与贝叶斯公式是两个相辅相成的互逆的运算公式,它对解决实际生活中的概率问题起着很重要的作用,在我们生活中的应用也相当广泛,灵活掌握全概率公式与贝叶斯公式,可以帮助中学生拓宽视野,提高数学思维能力和探究未知世界的兴趣.