关注抽象函数 提升核心素养——透视高考卷中的抽象函数问题

北京师范大学盐城附属学校 (224007) 郝文华

抽象函数问题是考查学生数学抽象素养的有效载体,近年来,高考数学试卷中频繁出现抽象函数问题,题目常涉及到函数的基本性质(奇偶性、周期性、对称性、单调性等)、函数图像、不等式、复合函数、导函数等基本内容,同时还蕴含着数形结合、函数与方程、化归等数学思想.由于抽象函数仅仅给出函数某种性质或满足某种关系,学生在解决此类问题时,常常感到束手无策、不知所措.要解决此类问题,需要把握数学本质,整合题目条件,注重解题的整体性和融合性.本文以近年高考中出现的相关试题为例,分析抽象函数问题常见类型及解题思路,供参考.

类型一 常规赋值法与图像法

例1 (2017新课标Ⅰ理)函数f(x)在(-∞,+∞)单调递减,且为奇函数．若f(1)=-1,则满足-1≤f(x-2)≤1的x的取值范围是( ).

A．[-2,2] B．[-1,1] C．[0,4] D．[1,3]

思路简析：根据条件画出草图即可得出-1≤x-2≤1,继而得到满足-1≤f(x-2)≤1成立的x的取值范围为[1,3].或作为非解答题,不需要展示解题过程,可根据条件找一个符合要求的函数,用以实现抽象与具体之间的相互转换.例如,f(x)=-x满足题设条件,则由-1≤f(x-2)≤1得,-1≤-(x-2)≤1,故满足-1≤f(x-2)≤1成立的x的取值范围为[1,3].

例2 (2020新高考卷)若定义在 R 上的奇函数f(x)在(-∞,0)单调递减,且f(2)=0,则满足xf(x-1)≥0的x的取值范围是( ) .

A. [-1,1]∪[3,+∞) B. [-3,-1]∪[0,1]

C.[-1,0]∪[1,+∞) D. [-1,0]∪[1,3]

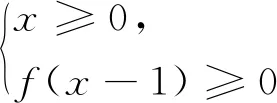
评注：此题也可利用例1中的解题思路进行解答.抽象函数问题尽管没有具体的函数解析式,但往往会给出一个非常开放的赋值条件,而赋值对象的选取是灵活多变的,具有强烈的指向性,所赋数值的选取通常也决定着解题的成败.

A. -3 B. -2 C. 0 D. 1

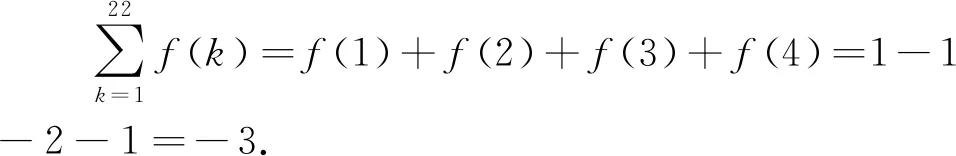
评注：在进行四次赋值的过程中,不仅实现了一些特殊函数值的求解,而且得出了函数的奇偶性和周期性,对于抽象函数基本性质的相互转化与应用,是近年高考常考的基本内容.

类型二 函数的基本性质相互转化

1.奇偶性与周期性问题

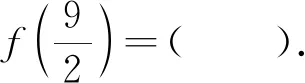
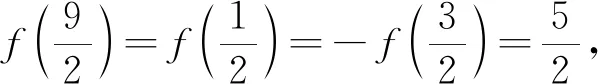
评注：如何理解f(x+1)、f(x+2)等复合函数的奇偶性呢?一般可从两个角度分析:一是从“形”的角度来看,函数y=f(x+1)的图象是由函数y=f(x)图象左移1个单位而得到,左移1个单位后是奇函数(即关于原点(0,0)成中心对称),因此,很容易得出函数y=f(x)的图象关于点(1,0)成中心对称.同理可得,由函数f(x+2)为偶函数(即关于y轴成轴对称)可以得出函数y=f(x)的图象关于直线x=2成轴对称.二是从“量”的角度来看,函数h(x)=f(x+1)为奇函数,则有h(-x)=-h(x),即f(-x+1)=-f(x+1);同理,对偶函数g(x)=f(x+2),有f(-x+2)=f(x+2).本例还可以从条件入手,直接由等式的实质进行推导.因为一般有以下关系:

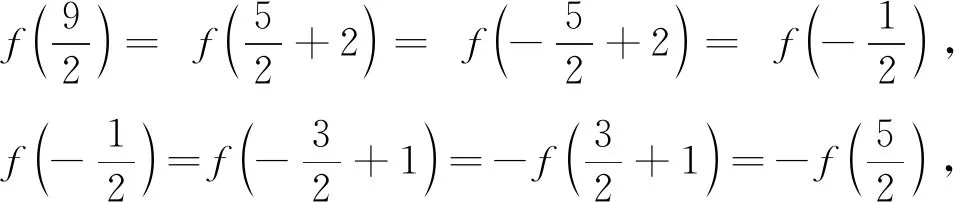
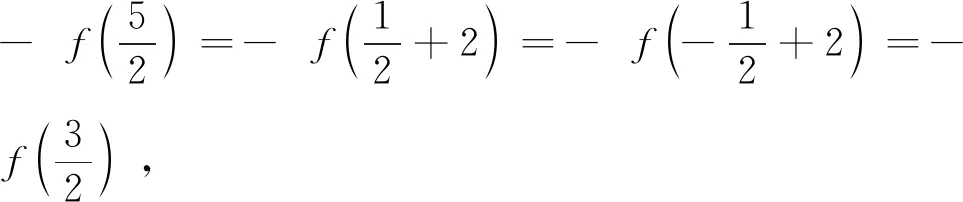
例5 (2021新高考Ⅱ卷)已知函数f(x)的定义域为R,f(x+2)为偶函数,f(2x+1)为奇函数,则( ).

C.f(2)=0 D.f(4)=0

思路简析：因为函数f(x+2)为偶函数,则f(2+x)=f(2-x),可得f(x+3)=f(1-x),因为函数f(2x+1)为奇函数,则f(1-2x)=-f(2x+1),所以f(1-x)=-f(x+1),f(x+3)=-f(x+1)=f(x-1),即f(x)=f(x+4),故函数f(x)是以4为周期的周期函数,因为函数F(x)=f(2x+1)为奇函数,则F(0)=f(1)=0,f(-1)=-f(1)=0,其它三个选项未知.故选B.

2.奇偶性与对称性问题

A. -21 B. -22 C. -23 D. -24

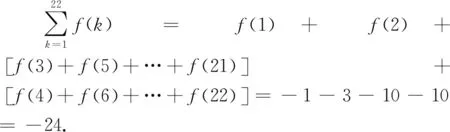
评注：一般情况下,含有对称轴或对称中心的问题往往条件比较隐蔽,求解时需要根据已知条件进行恰当的转化,然后再获得所需的一些数值或关系式.

3.奇偶性、对称性与周期性的综合问题

例7 (2018全国Ⅱ理)已知f(x)是定义域为(-∞,+∞)的奇函数,满足f(1-x)=f(1+x)．若f(1)=2,则f(1)+f(2)+f(3)+…+f(50)=( ).

A． B．0 C．2 D．50

思路简析：因为f(x)是奇函数,且f(1-x)=f(1+x),所以f(1+x)=-f(x-1).∴f(3+x)=-f(x+1)=f(x-1),∴T=4,因此f(1)+f(2)+f(3)+…+f(50)=12[f(1)+f(2)+f(3)+f(4)]+f(1)+f(2),因为f(3)=-f(1),f(4)=-f(2),所以f(1)+f(2)+f(3)+f(4)=0,∵f(2)=f(-2)=-f(2)∴f(2)=0,从而f(1)+f(2)+f(3)+…+f(50)=f(1)=2.故选C.

评注：函数的奇偶性与周期性相结合的问题多考查求值问题,常利用奇偶性及周期性进行变换,将所求函数值的自变量转化到已知解析式的函数定义域内求解.

类型三 抽象函数与导数、不等式的综合性问题

C.f(-1)=f(4) D.g(-1)=g(2)

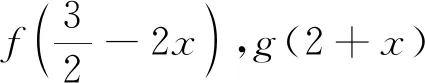
评注：解决本题的关键是转化题干条件为抽象函数的性质,准确把握原函数与导函数图象间的关系,结合函数的性质(必要时结合图象)即可得解.

函数是中学数学学习中最为重要的内容之一,教学中应注重知识的整体性、融合性及互通性,避免知识的碎片化、独立化;引导学生从不同视角深入探究,找规律,充分挖掘问题背后隐性的价值和内涵,把握数学内容的本质.同时,还要研究新高考试题的考查方向和角度,为实施精准教学创设条件.