新高考所引发的数学复习教学的焦虑及对策
2023-05-10江苏省盐城市第一中学224000孙蓉蓉
江苏省盐城市第一中学 (224000) 孙蓉蓉
近年,全国不少省份实施新高考模式,很多省份的高考命题都采用全国Ⅰ卷,高考命题也不再提供考试说明等参考材料,而是“依据高中课程标准,参考高考评价体系”进行命题,这些改变让很多一线教师一时无所适从,从而引发了对数学解题教学的各种焦虑.
1 引发焦虑的原因
1.1 高考评价体系发生改变
2020年1月,教育部考试中心发布了《中国高考评价体系》(下称体系).“体系”由“一核”“四层”“四翼”组成, “一核”回答了“为什么考”的问题,即为了服务“立德树人、服务选材、引导教学”核心功能;“四层”回答“考什么”的问题,即考查“基础知识、关键能力、学科素养、核心价值”;“四翼”回答了“怎么考”的问题,即要在考查中体现“基础性、综合性、应用型、创新性”. 显然,新高考的命题已经由“知识立意、能力立意评价”向“价值引领、素养导向、能力为重、知识为基”的综合评价转变,对学生的考查做到“知识点全覆盖”,这就意味着教师较难预测到什么是重点考查内容、什么内容不考,从根本上杜绝了猜题、押题的可能性.
1.2 高考命题方向发生改变
从试题结构上看,全国Ⅰ卷由“8道单项选择题、4道多项选择题、4道单空填空题及6道解答题”组成.从近年来试卷难度分析,全国Ⅰ卷中的中档题居多,基本没有送分题,而且“层层设卡,步步有难”,学生不容易拿到分数,再加上多项选择题和结构不良试题的引入,更是增加了学生的思维量与运算量.从考查的重点来看,全国Ⅰ卷遵循的命题原则是“重点必考,主干多考,次点轮考,补点选考”,也就说“每个知识点都是潜在的压轴题”.从解答题的分布情况分析,全国Ⅰ卷不仅增加了考查“概率统计”的解答题,而且解答题的先后顺序不固定,这就意味着任何一类题都有可能充当压轴题的“角色”,这就导致复习的重心很难把握.不仅如此,全国Ⅰ卷增加了应用问题的考查力度,增加了以数学文化为背景问题的考查,试卷的阅读量大幅度增加,从而导致考生很难适应.
2 解题教学中的各种“焦虑”
“数学学习意味着要善于解题”,而解题教学是恰恰提升学生解题能力的主要途径和必要手段.新高考不可避免的给广大教师带来各种焦虑,而这种情绪也直接反映在解题教学上.
2.1 担心命题方向拿不准,“拿来主义”来应对
新高考命题不再提供考试说明与考试大纲,完全以课程标准为依据,命题的方向不如以前那么明确,充满着各种变数与可能性,出于这样的焦虑,“拿来主义”开始在数学解题教学中盛行.具体表现为,教师搜罗各种网站、微信公众号等试题资源,把各地的模考或联考的试题奉为“至宝”,以为这些试题就代表着高考命题的方向,因此不加选择的把这些试题作为解题教学的素材、研究的重点.教师往往忽视分辨与选择这一深加工过程.
2.2 担心方法不够有效,“二级结论”来充数
新高考总体运算量加大,基础题、中档题、难题的分布由原先的6:3:1变化为现在的3:6:1.由于担心学生做不完,很多老师开始怀疑“通性通法”是不是够用,于是就把教学的重心放在传授“二级结论”上,例如,“极线方程”“三余弦定理”“泰勒展开”“切比雪夫不等式”等,还有各种数列放缩公式、圆锥曲线中重要性质等一并抛给学生.尽管“二级结论”的应用在某些时候可以让学生更快的获得正确答案,表面上看似提升了解题效率,但实际上对学生解题水平的提升帮助有限,“二级结论”补充的越多,学生越不堪重负.
2.3 担心接触题型不够多,“偏题、怪题”齐上阵
在新高考中,考查数学建模能力、阅读理解能力、数学探究能力的题型会大量出现,这些题型看上去往往比较新,由于担心学生没有接触过而不会做,很多教师把大量的精力放在对这类题的研究上.而忽视真正领悟这类题型的命题思想,特别是随意编造问题情境,人为地增加学生理解的难度,或者篡改数据,故意增加运算繁琐程度,更甚者把原本属于解答题的题型直接变成填空题或者多选题,于是创造出一系列的“偏题、怪题”. 在实际教学中,这些“偏题、怪题”并不能被学生掌握,反而也会增加学习的“焦虑”.
3 新高考下数学复习教学应然策略
3.1 重视关键能力的培养
高考数学主要考查的关键能力有:阅读理解能力、信息整理能力、语言表达能力、逻辑思维能力、批判性思维能力、应用实践能力和创新能力等.关键能力是构成数学素养的核心要素,是高考重要的考查目标,是测试和评价的核心指标.其关系可表述为:
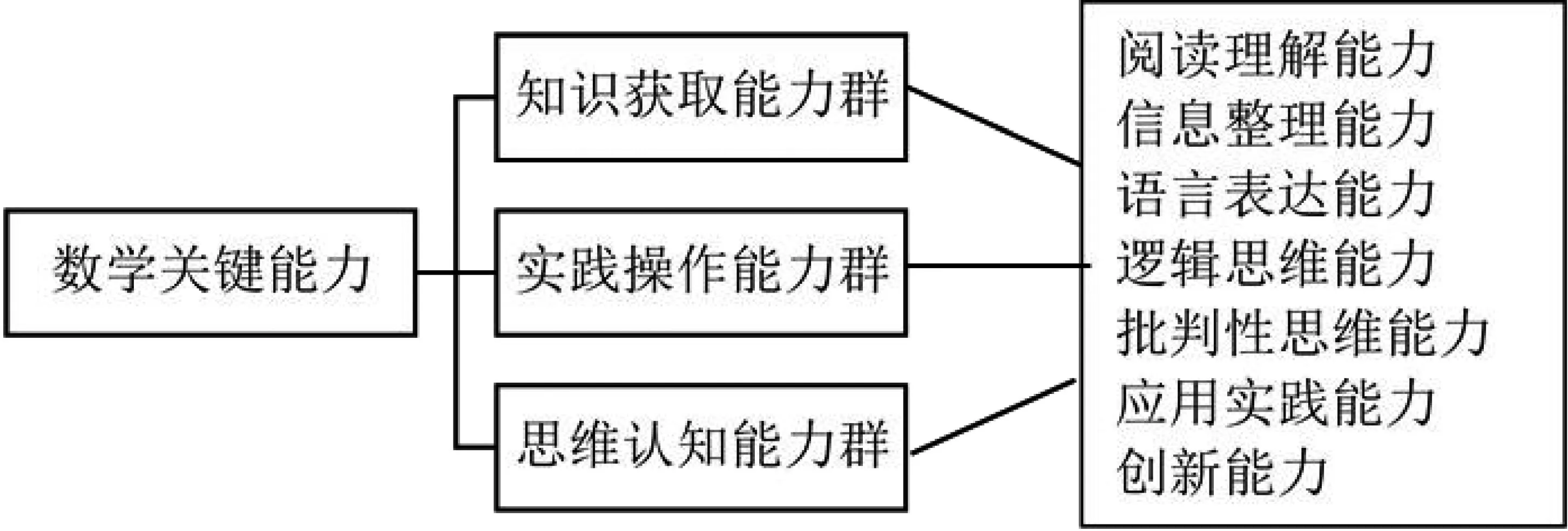
图1
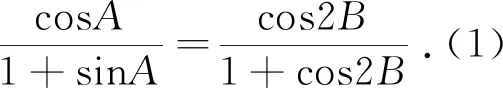
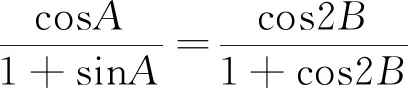
3.2 重视对概念的再认知
在传统的解题教学中,广大师生热衷于“刷题”,这种“以题为中心”的教学观很容易使解题教学陷入“题海”不能自拔.要知道,概念才是数学的核心,解题充其量只是概念的衍生与应用,若没有概念作为基础,解题与解题教学也就无从谈起.
例2 (2022年新高考Ⅰ卷第2题)若i(1-z)
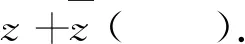
A.-2 B.-1 C.1 D.2
评析:此题的通法是设z=x+yi(x,y∈R),再通过解方程的思想求出x,y的值.但如果认识到i2=-1这个基本事实,就很容易知道1-z=-i,根本不需要怎么运算.为什么很多学生认为高考计算量大?其中的一个主要原因就是没有把数学问题与数学概念联系起来,没有把问题的本质搞清楚.
3.3 重视问题解决教学
在问题解决教学中,应培养学生自己提出问题、建立假设、设计研究过程来验证假设和解决问题能力,让学生以自主学习的方式进行问题的探索与解答.
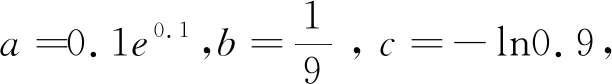
A.a 高考作为教育评价的关键环节,其选拔性是基本功能之一,而育人才是其核心功能.因此,教师应深入研究教学,深入研究命题,以帮助学生形成和完善认知结构、发展核心素养为根本任务.