找准复习着力点 促进思维进阶*

福建省福州市闽清县第一中学 (350800) 卢秋丹

高考命题已经从能力立意转到素养导向,素养导向的高三复习课教学要求数学教师激发学生的主观能动性,引领学生对所学的知识与方法进行梳理、归纳,使数学知识系统化;引领学生站在学科思想的高度深层次的认识数学本质,培养学生深度学习的良好习惯.然而,不少高三复习课往往只重视“题海”训练,学生机械模仿,大量“刷题”,这种“低思维”的复习模式,不仅师生双方觉得疲惫不堪,而且不利于学生独立思考,不利于学生学科核心素养的提升.要让学生适应新高考的要求,教师应充分利用课堂的黄金时间,引领学生对高中数学知识、思想方法再认识、再提高, 追求更深层次的理解;引领学生通过对典型问题的主动探究,完善学生的认知系统和思维系统,提升学生自觉运用所学的知识和方法分析问题与解决问题,使体现学科本质、具有深度思维价值的课堂活动真正发生,从而提升学生关键能力,促进数学核心素养落地.

1 打通知识与问题的联结点,提升认知高度

高三一轮复习教学,不是简单罗列高一、高二所学知识、梳理方法、唤醒学生对所学知识的记忆,更要站在系统的高度,引导学生以主干知识为主线,以教材为依据,对所学知识“联珠编网”,整合内容板块,促进知识的系统化、网络化;引导学生站在整体的高度与教材对话,弄清知识之间的逻辑关系,完善数学认知结构;帮助学生打通知识与问题之间的联结点,使他们由问题能联系到所学的知识,由知识会联想到问题,提升认知高度.

案例1 课本对“数列”知识是以线串式顺序呈现的,在复习教学中,教师可以将“数列”内容进行重组, 用思维导图的形式展示这一章节内容的内在结构(如图1),使学生对该单元内容的逻辑链条有一个直观的、整体的、清晰的认识,从而实现结构化思维的培养.

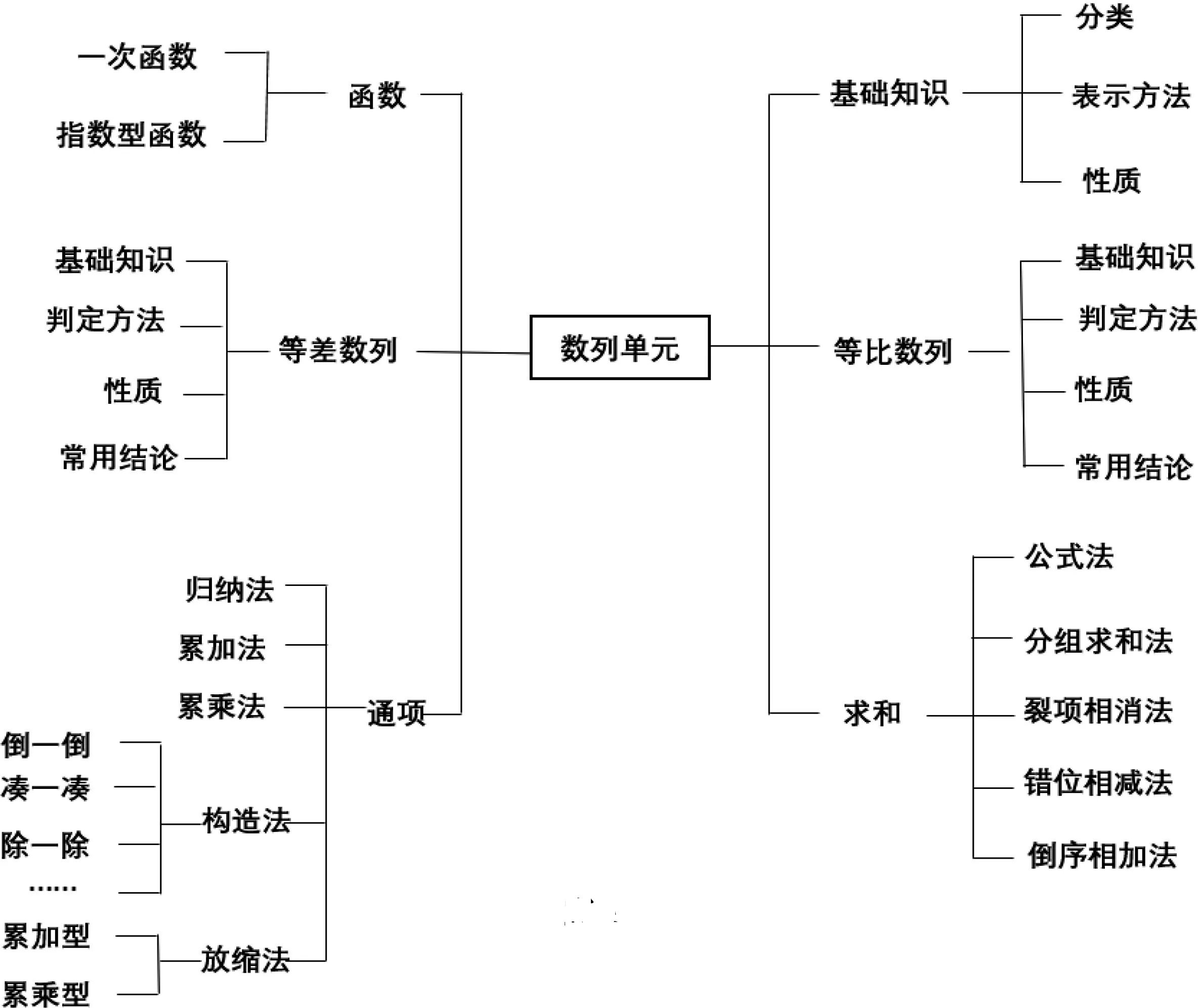
图1

不少教师在复习各章节知识时,对公式、定理的推导过程一带而过,只强调需熟记公式,然后就进行大量的训练.学生不了解知识的来龙去脉,就无法完整地建构知识体系,更无法体会定理、公式等规律在推导过程中所揭示的数学思想方法.因此,在一轮复习教学中,教师应精心设计恰当的问题串,引导学生重温公式、定理的推导过程,并重视其思维过程的呈现,让学生在数学思想方法的体悟中,发展思维,提升关键能力.笔者以“等比数列的前n项和公式”为例,设置以下问题串:

问题1 请回顾“等比数列的前n项和公式”(强调需分q=1和q≠1两种情况.)

问题2 课本是怎样推导公式的,推导过程蕴涵着哪些数学思想方法?(强调“减元”思想.)

问题4 还有其他推导的方法吗?

问题5 请类比“等差数列前n项和公式”的推导方法“倒序相加法”,它们有何相同之处?(本质一样, 目的都是“消项”,使无限化归为有限.)

在公式、定理等规律的生成过程中,体现了数学先哲们的思维方式、解决问题的方法,回归课本,重温公式、定理的推导过程,把握知识的来龙去脉,有利于学生深刻领悟蕴涵其中的数学思想方法,优化思维品质,提升思维深度.

2 以“暴露问题”为重点,促进思维进阶

在高三数学复习中,“错题”是教学的一个顽症.学生做错题的原因多种多样,一些是由于对概念、公式、定理产生理解上的偏差造成的,另一些则是审题不当、运算出错等原因.因此,教师应不失时机地为学生搭建“纠错”的平台,把典型的“错题”作为蓝本,经过变式,设计成带有变化性与延展性的问题,有针对性引导学生纠正偏差,突破思维障碍.改编“错题”的方式有转换问题的条件与结论、变化问题的情境、改变问题的设问方式等等.这样的改编题在形式上与“错题”有区别,能使学生带着新鲜感做题,具有潜移默化的纠偏功效,可提高学生对错误的“免疫力”.具体做法是“错题——交流——归因——变式——反馈——小结.其中交流就是通过与做错题目的学生交流,寻找隐藏在错误背后的知识缺漏与思维缺陷.“错题”改编后的反馈环节是检查学生是否达到了纠错的目的,小结环节具有一定的延展性,例如进行方法总结、获得一般性结论等,最终实现“识错、纠错、防错”的目标,促进学生思维进阶.

案例2 已知数列{an}的前n项和为Sn,an≠0,a1=1,anan+1=2Sn-3(n∈N*),求数列{an}的通项公式.

多媒体展示典型错解:由于anan+1=2Sn-3(n∈N*)⑴,因此an+1an+2=2Sn+1-3 ⑵,由⑵-⑴得an+1(an+2-an)=2an+1,因为an+1≠0,所以an+2-an=2,因此数列{an}的奇数项和偶数项分别是公差为2的等差数列,故数列{an}是公差为1的等差数列,又a1=1,因此an=n.

师:以上解法对吗?

学生讨论、交流后发现,上述解法对等差数列定义的理解出现偏差,没有运用等差数列的定义进行推理,误以为数列的奇数项和偶数项都为等差数列且公差相等时,数列就是等差数列.通过探究,学生得到了正确解法.

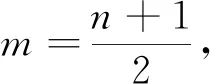
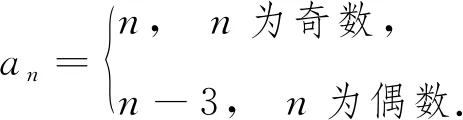
案例2中,教师有效利用“错误资源”,充分发挥学生的主体地位,引导其相互交流,在问题分析中暴露思维,在识错与纠错中修正错误,在智慧变题中发散思维,让学生对问题有了深度理解,为了强化学生对知识的理解,让学生真正地纠正偏差,教师给出如下变式:

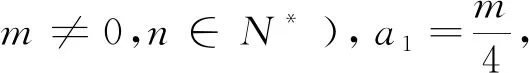
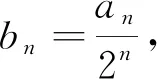
变式3 数列{an}满足an+1+(-1)nan=2n-1,则{an}的前12项和为.

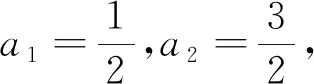
师:从以上例题与变式可得到什么启示?

学生交流、归纳:⑴定义是证明数列为等差数列(或等比数列)的最基本方法;⑵如果某数列的奇数项与偶数项分别是公差相同的等差数列,且这个数列的前三项成等差数列则该数列一定是等差数列.

3 以解题反思为生长点,促进深度正迁移

许多教师在讲完一个问题后,往往没有给学生反思的时间,而是根据自己的教学经验,直接指出该题的题眼、陷阱以及运用的思想方法等等.学生虽然听懂了,但并没有内化为自己的知识,无法留下深刻的印象.因此教师应给予学生自主反思、“顿悟”的时空,引导学生对解题的思维过程再思考、再认识,在深度反思中不断探询再生性知识的“生长点”,并形成具有个性化的经验,让高三复习收到事半功倍的效果.

案例3 过抛物线C:y2=2px焦点F的直线l与C交于A、B两点,且A、B两点的纵坐标分别为y1,y2,求证:y1y2=-p2.

经过探究,学生得到了该题的不同解法,教师多媒体展示以下三种方法.

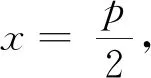
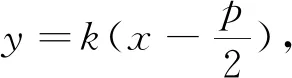
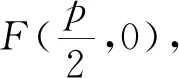
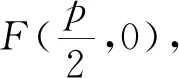
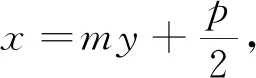
接着,教师让学生进一步反思:

反思1 该题的逆命题能否成立?即:直线l与抛物线C:y2=2px(p>0)交于两点,且两交点的纵坐标为y1,y2,如果y1y2=-p2,则直线l是否过C的焦点?

反思2 若改变例题的条件,是否可以获得相似的推论?即:设直线l过定点(t,0)且与抛物线C:y2=2px(p>0)有两个交点P、Q,P、Q两点的纵坐标分别为y1,y2,则y1y2是否为定值?

反思3 设直线l与抛物线C:y2=2px(p>0)有两个交点P、Q,P、Q两点的纵坐标分别为y1,y2,且y1y2=m(m为常数),则该直线l能否过定点?

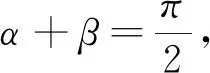
反思5 设直线l与抛物线C:y2=2px(p>0)有两个交点P、Q,直线OP与OQ的倾斜角分别为α、β,若α+β=θ(θ为定值且θ∈(0,π)),则直线l能否过定点?

通过层层递进式的反思,学生的思维激流涌动,产生了学习数学的“好胃口”,促进其主动对解题过程进行深层次分析,对解题过程中所用到的数学思想方法进行归纳、提炼,进而产生新的想法,展开新的探索,“生长”出新的问题.

在问题解决后,教师应有意识地引导学生进行如下反思:⑴本题的背景是什么?解题的难点在何处?是如何化归的?今后应怎样思考这一类题目?⑵解题过程中哪几个步骤容易出错?怎样预防与克服?⑶该题还有其他方法吗?其中哪一种方法比较基本?哪一种方法比较巧妙?哪一种更简便?分别有哪些可取之处?⑷命题能否进行变式、延展?⑸解决问题的过程中运用了哪几种思想方法?运用这些方法应该注意哪些问题?

引导学生对自身的思维过程进行再思考、再认识,养成多归纳、勤总结的良好习惯,有利于实现知识结构的内化,在解决问题的过程中建构知识树、生成知识林,逐步形成“无论研究对象如何变化,研究方法与研究套路不变”的切身体会,有效促进学生知识和能力的高效正迁移.

总之,高三数学复习是一个不断夯实必备知识、落实数学核心素养、提升关键能力的过程,教师应全力打造“重学生参与、重知识建构、重思维活动”的魅力课堂[3],让知识问题化,问题序列化,为学生数学行为的健康、有序发展提供潜在的“加速度”,从而促进学生高阶思维能力的“生长”,最终形成数学关键能力.