让数学课堂更多一些理性
——加强学生理性思维培养的几点设想
2023-05-10江苏省南通市通州区平潮初级中学226361陆春霞
江苏省南通市通州区平潮初级中学 (226361) 陆春霞
理性思维是指以概念、判断和推理为基本形式的思维,是建立在证据和逻辑推理基础上的一种思维方式.初中阶段数学课程从算术转向代数、从常量走向变量、从直观实验过渡到严密抽象的逻辑推理,是培养学生思维从感性认知走向理性发展的关键时期.2022年版《义务教育数学课程标准》指出“数学在形成人的理性思维、科学精神和促进人的智力发展中发挥着不可替代的作用”,并从“用数学的思维方式思考现实世界”的层面对初中学生理性思维的培养提出了具体要求.作为学生核心素养的重要组成部分,广大一线初中数学教师必须对理性思维的培养引起足够的重视.那么,落实到操作层面,如何在数学课堂教学中加强初中学生理性思维培养呢?笔者认为可以从以下几个方面着手:
一、引导学生探究自然现象或现实情境所蕴含的数学规律,经历“再发现”的思维过程
数学是对客观世界(自然现象或现实情境)的抽象反映.抽象的过程是一个去伪存真、去粗存精的提炼过程,数学规律的发现本身就蕴含着理性的思考.因此,在教学中引导学生探究自然现象或现实情境所蕴含的数学规律,经历“再发现”的思维过程是培养学生理性思维的极佳载体.
比如,在讲授人教版《数学 七年级上》§1.3.2中“有理数的减法法则”时,可以先借助具体情境:北京某天的气温是4°C~10°C,这一天北京的温差是多少?接着追问:若北京某天的气温是-2°C~4°C,这一天北京的温差又是多少?学生潜意识中会很快地给出答案:温差是6°C.再追问:为什么也是6°C?你是怎么得到的?学生会在数轴上画出对应的点给“数”出来.这时,话锋一转,温差就是最高气温减最低气温,即4-(-2),也就是正数与负数的减法问题,你能从运算的角度加以解释吗?引导学生发现:根据减法是加法的逆运算,计算4-(-2),就是要求出一个数x,使得x与-2相加得4,因为6与-2相加得4,所以x应该是6,即4-(-2)=6;另一方面,我们知道4+(+2)=6,所以就得出4-(-2)=4+(+2),即减-2相当于加2.然后教师和学生共同探究:①把4换成0,-1,-5,用上面的方法进一步考虑这些数减-2的结果与它们加+2的结果相同吗?②计算9-8,9+(-8);15-7,15+(-7).从中又有什么发现?通过以上探究,让学生进一步发现,有理数的减法可以转化为加法来进行,从而得出有理数的减法法则:减去一个数,等于加这个数的相反数.
二、引导学生理解数学新旧知识的内在本质与联系,养成“刨根究底”的思维习惯
数学是由基本数学概念和法则架构而成的一个知识网络系统.这些知识(概念、法则)间往往有着千丝万缕的内在必然联系.教学中,应通过引导学生理解新授概念(法则)与其认知结构中原有的数学概念(法则)内在本质与联系,通过追问引导学生“刨根究底”,大胆质疑问难,进而把新授概念(法则)同化到已有的认知结构当中(或者改组扩大原有的认知结构,将新授概念(法则)纳入进去),从而厘清新授概念的内涵与外延、明确法则的条件结论与来龙去脉,逐步领悟到新授概念(法则)的本质和规律.
比如,人教版教材《数学 九年级上》§21.1一元二次方程的教学.前面学生已经学习了一元一次方程的解法,对利用运算律和等式的基本性质通过去括号、移项、合并同类项求解已经得心应手;另外,学生业已掌握二元一次方程组和三元一次方程组的解法,知道可以通过“消元”转化为一元一次方程.从数学知识内部发展来看,二元、三元一次方程组可以视为一元一次方程在“元”上的推广.引导学生思考:一元二次方程可以视为一元一次方程在“次数”上的推广.那么,可否将一元二次方程转化为一元一次方程?学生自然想到“降次”,将“二次”降为“一次”.如何降次?通过具体实例引导学生从最简单的二次方程x2=p(p>0)的情形入手,再拓展为(x+n)2=p(p>0)的情形,最后推广为一般形式ax2+bx+c=0,让学生从简单的、特殊的入手,通过逐步推广而获得一般性问题的求解方法.引导学生将未知问题转化化归为熟悉的问题,在尝试解决的过程中思维不断地发生碰撞,并从中感悟二元一次方程与一元一次方程、平方根之间的内在联系.学生在刨根究底中蓦然发现二元一次方程求解实质上就是解决如何开平方!
三、引导学生合乎逻辑地解释或论证数学的基本方法与结论,铸成“推理有据”的思维品质
陈建功先生说过:“推理之成为说理的体系者,限于数学一科”,“忽视数学教育论理性的原则,无异于数学教育的自杀”.可以说,推理是数学的命根子.合乎逻辑的推理是得到数学结论、构建数学体系的重要方式,是数学严谨性的基本保证,也是人们在数学活动中进行交流的基本思维品质,在形成人类的理性思维方面起着核心的作用.因此,在解释或论证数学的基本方法与结论时,要尽可能地引导学生经历问题求解的逻辑思路探索过程,通过归纳和概括方法引导学生经历合情推理转向逻辑推理,并在分析的基础上通过演绎的方式,使解释与论证思路具体化和规范化;使学生养成合乎逻辑地解释与论证数学基本方法与结论的思维习惯,铸成“推理有据”的思维品质.
比如,在讲授人教版教材《数学 八年级上》§11.2.1中三角形内角和定理时,引导学生回忆:小学里通过度量或剪拼的方法可以验证“三角形的内角和等于180°”.但是,由于测量常常有误差,这种“验证”不是“数学证明”,这样得出的结论缺乏说服力,不能完全让人信服;更何况形状不同的三角形有无数个,我们不可能用度量或剪拼的方法一一加以验证.因此,要确认“三角形的内角和等于180°”,就不能只依赖度量或剪拼的手段和观察、试验、验证的方法,让学生从心底里认同推理论证的必要性.那么,如何论证“任意一个三角形的内角和都等于180°”呢.我们的依据是前面学习过的概念、基本事实与定理.引导学生审视剪拼的过程(由图1到图2),发现只需过点A作边BC的平行线EF(如图3)即可.
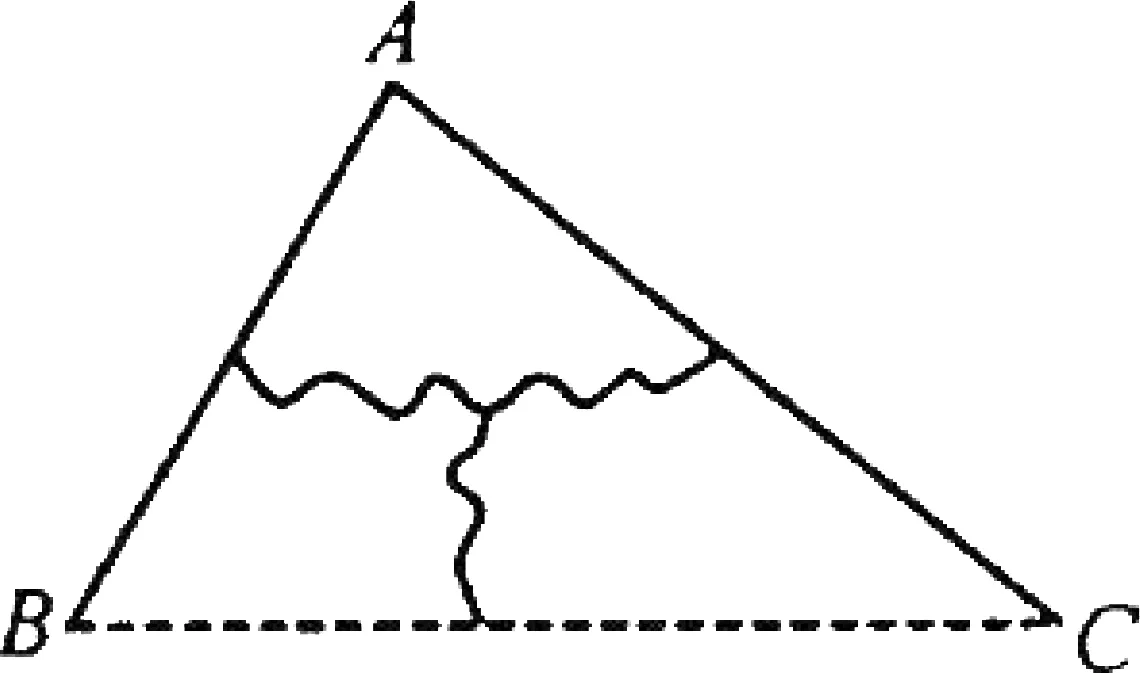
图1
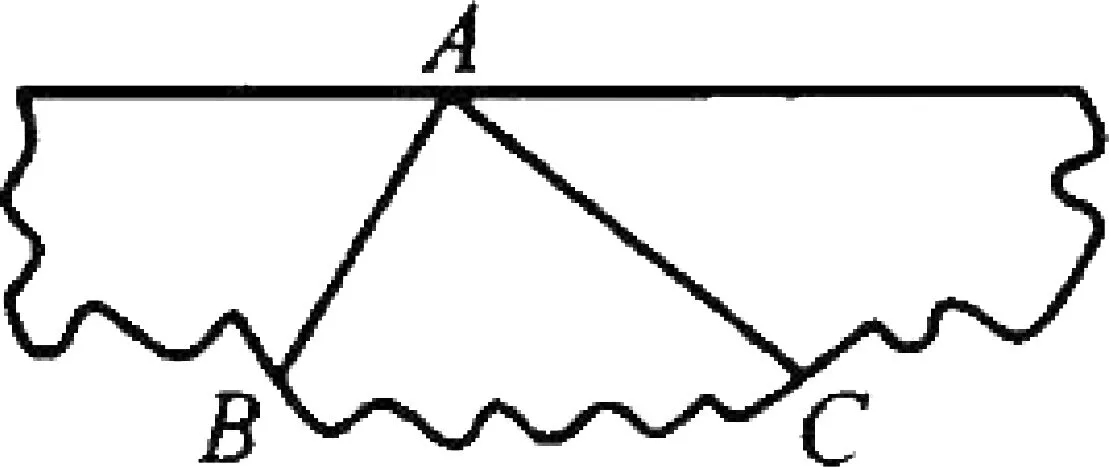
图2
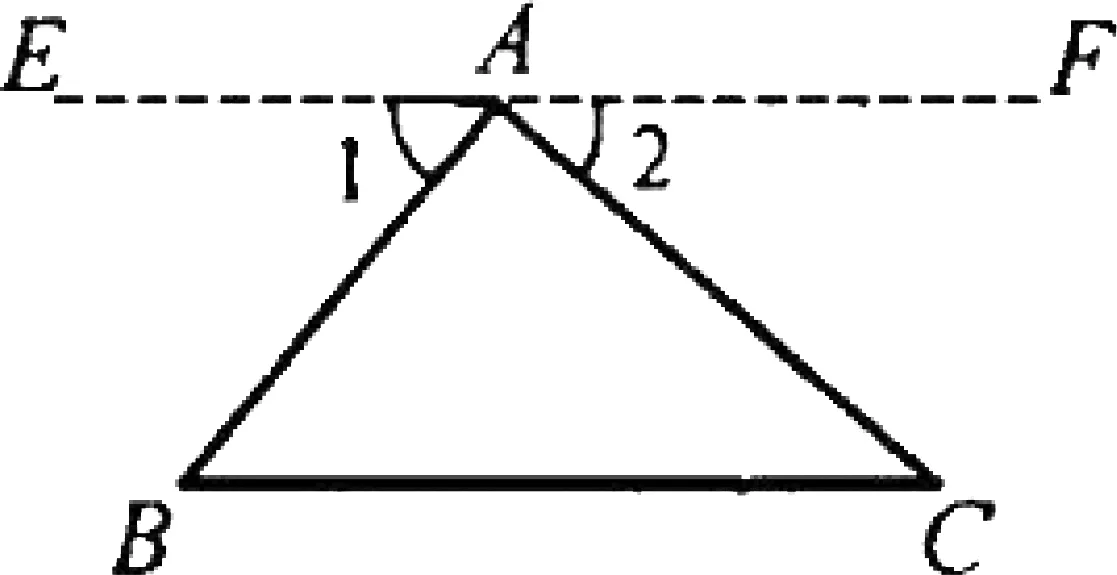
图3
师生共同完成证明过程的书写.
已知△ABC,求证:∠A+∠B+∠C=180°.
证明:如图3,过点A作直线EF,使EF//BC.
∵EF//BC,∴∠1=∠B(两直线平行,内错角相等).同理∠2=∠C.∵∠1,∠BAC,∠2组成平角,∴∠1+∠BAC+∠2=180°(平角定义).∴∠B+∠BAC+∠C=180°(等量代换).即∠A+∠B+∠C=180°.
上述推理采用的是三段论的演绎方式,这也是演绎推理的一般模式,包含大前提(概念、基本事实或定理等一般原理)、小前提(所研究的特殊情形)和根据一般原理对特殊情形作出判断所得的结论.大前提是显然的可以省略,这样每组“因为……,所以……”就构成了一个基本的推理单元.让学生体悟到通过这样的方式实现推理过程步步有据,因而结论是可信的.
总之,让数学课堂更多一些理性,通过引导学生探究自然现象或现实情境所蕴含的数学规律,经历“再发现”的思维过程;通过引导学生理解数学新旧知识内在本质与联系,养成“刨根究底”的思维习惯;通过引导学生合乎逻辑地解释或论证数学的基本方法与结论,铸成“推理有据”的思维品质;培养学生崇尚真知,尊重事实和证据,形成严谨清晰的理性思维,从而运用理性思维方式去认识事物、解决问题、指导行为,形成严谨求是的科学态度与理性精神.这是培育学生数学核心素养的重要落脚点,也是落实数学学科育人的价值所在.
