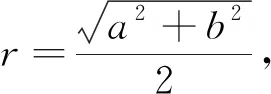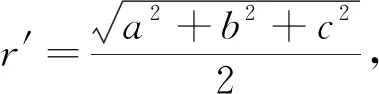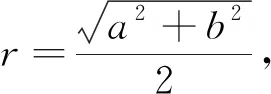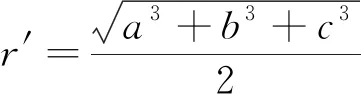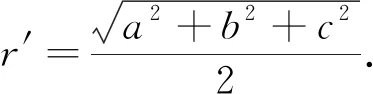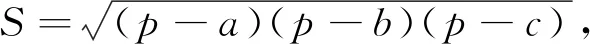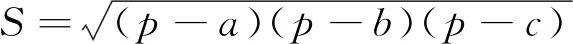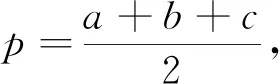减少失分的有效策略
——检验*
2023-05-10江苏省扬州中学225009徐孝慧
江苏省扬州中学 (225009) 徐孝慧
江西省扬州市教育科学研究院 (225007) 戚有建
*本文是江苏省教育厅跟进式改革重大研究项目《区域高中生数学学业质量检测支持系统的实证研究》(编号:2019jyktzd-12)的阶段性研究成果.
在平时的学习过程中,很多学生的解题习惯是一遍做完、从不检验.实际上根据波利亚的解题表,解题过程包括四个步骤:弄清题意、拟定计划、实现计划、回顾反思,其中的回顾反思指的就是解题后的检验.所谓百密一疏,解题过程中有时错误是难免的,此时如果有检验的习惯和方法,可以及时发现一些错误,减少失分.下面介绍四种常见的检验方法.
1.逆代检验
当问题的答案是有限个具体的数据时,可逐一代回进行检验,从而及时发现错误、避免失误、减少失分.
例1 已知集合A={a+1,a2+a},若2∈A,则实数a=.
分析:作为填空题,本题很容易错,结果容易出现多解.
错解:当a+1=2时,a=1;当a2+a=2时,a=1或a=-2,综上得:a=1或a=-2.
点评:结果出现两解,可能会引起我们的关注,此时如果有检验的意识和习惯,可以及时发现错误,减少失分.逐一代回检验后发现:当a=1时,a+1=2,a2+a=2,与集合元素的互异性矛盾,此时不符合要求;当a=-2时,a+1=-1,a2+a=2,此时符合要求.
错因:忽视了集合元素的互异性
例2 若函数f(x)=x3+(a-1)x2-x+a2-1是奇函数,则实数a=.
分析:很多学生喜欢用f(0)=0处理,导致结果出现多解.
错解:因为函数f(x)是奇函数,所以f(0)=0,即a=±1.
点评:结果出现两解a=±1,此时如果有检验的意识和习惯,可以及时发现错误,减少失分.逐一代回检验后发现:当a=1时,f(x)=x3-x,是奇函数,符合要求;当a=-1时,f(x)=x3-2x2-x,不是奇函数,此时不符合要求.
错因:“f(0)=0”不是“f(x)=x3+(a-1)x2-x+a2-1是奇函数”的充要条件,实际上仅仅是必要不充分条件.
2.特殊化检验
当问题是全称命题或者恒等式时,可取特殊值代入检验,从而及时发现错误,减少失分.
例3 求和Sn=1×21+2×22+…+n×2n.
分析:多数学生知道用错位相减法处理,但是很多学生算不到正确结果.
错解:由于运算过程中的失误,学生会出现各种错误结果,例如学生1:Sn=1×21+2×22+…+n×2n=(n-1)2n+1;学生2:Sn=1×21+2×22+…+n×2n=(n-1)2n+2;……
点评:此时如果有检验的意识和习惯,可以及时发现错误,减少失分.特殊化检验后发现:当n=1时,学生1的S1=0,显然错误;当n=2时,学生2的S2=6,显然错误.
正解:Sn=1×21+2×22+…+n×2n=(n-1)2n+1+2.
拓展:本题为什么可以特殊化检验?因为数列求和是关于n的恒等式,即等式1×21+2×22+…+n×2n=(n-1)2n+1+2对任意的n都成立.
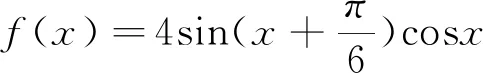
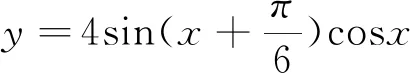

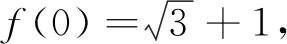
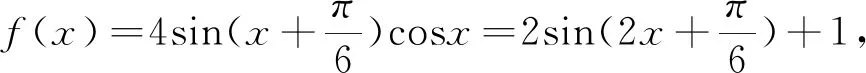
3.极端化检验
当常规情况难以确定时,可考虑极端情况、极限情况进行检验,从而及时发现错误,减少失分.
例5 若a,a+1,a+2是钝角ΔABC的三边长,则实数a的取值范围是________.
分析:容易想到从钝角出发构建不等式,却容易忽视三角形中隐含的不等式.
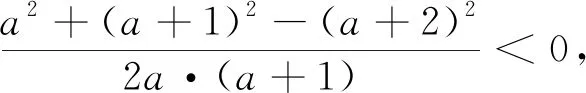
点评:此时如果有检验的意识和习惯,可以及时发现错误,减少失分.极端化检验后发现:当a→0时,a,a+1,a+2→0,1,2,此时不能构成三角形.
错因:忽视了三角形中的不等式a+a+1>a+2,即a>1.
正解:1 分析:很多学生会从形式入手,猜想结果,有的猜2,有的猜3,盲目性很大. 对于有明显几何意义和物理意义的解题结果,量纲检验是非常有效的一种方法. 例8 在△ABC中,已知三边长为5,6,7,则此三角形的面积S=_________. 分析:很多学生喜欢用海伦公式处理,但由于海伦公式不作统一要求,所以学生对公式掌握不准确. 错解:由于对公式掌握不准确,学生会出现各种错误结果,例如 小结:解题过程中由于实施了非等价变形或者由于我们自身的失误,有时错误是难免的,如果有检验的习惯和方法,就能及时发现一些错误,不仅可以减少失分,而且可以养成及时反思和严谨的思维品质.
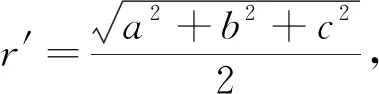
4.量纲检验(单位检验)