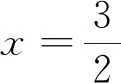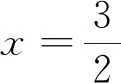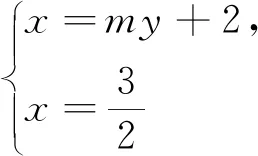识破伪装,看透本质——两道高考题的几何背景研究

浙江省杭州市富阳区江南中学 (311400) 林荣锋

1.试题展示

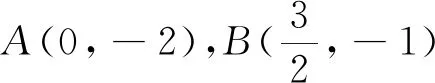
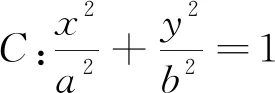
2.试题解答

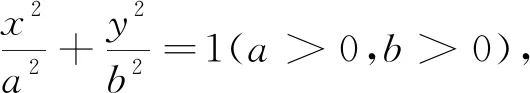
(2)由于题目没有交代M,N的位置关系,那么也就是说无论是N在上方还是M在上方,结论都是成立的,我们以点N在点M上方为例(如图1).

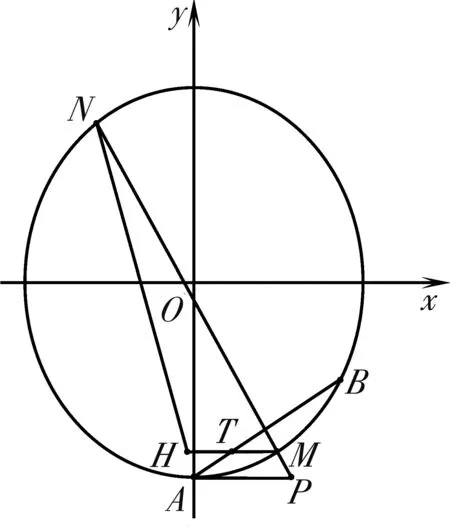
图1

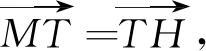
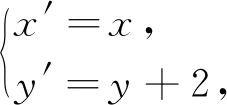
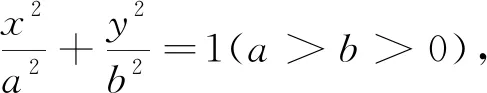
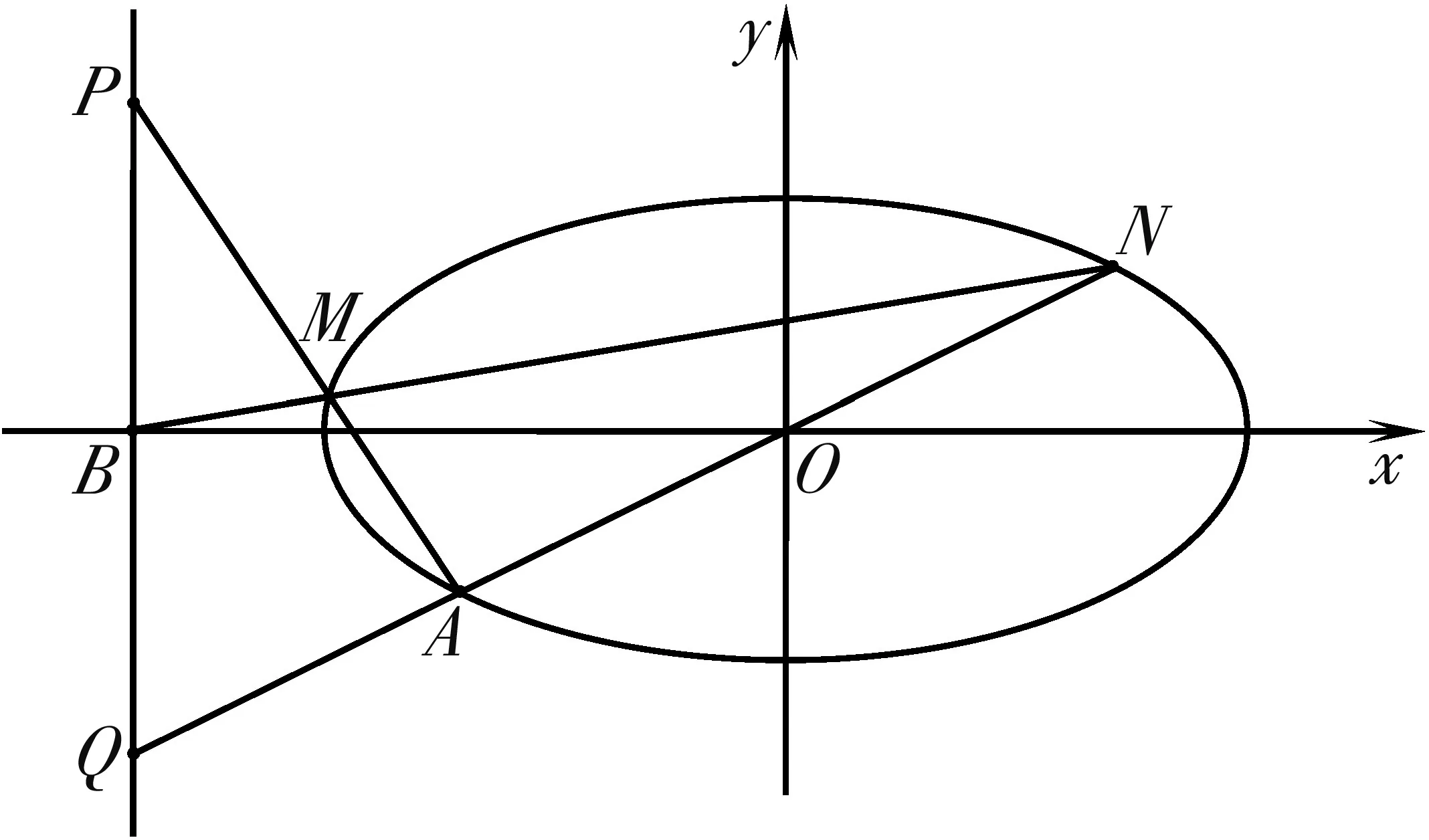
图2

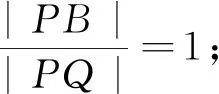
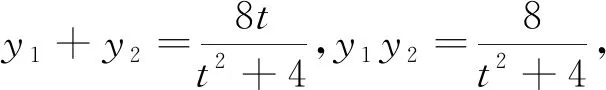
3.试题背景探究

两道试题均是以极点、极线、调和点列、调和线束为背景的问题.题1中,直线AB为P点对应的极线.题2中点B对应的极线为x=-2.下面给出相关的概念.

3.1 极点、极线的几何定义

如图3,设P是不在圆锥曲线上的一点,过P点引两条割线依次交圆锥曲线于四点E,F,G,H,连接EH,FG交于点N,连接EG,FH交于点M,则直线MN为点P对应的极线.若点P为圆锥曲线上的点,则过点P的切线即为极线.

图3

3.2 调和点列

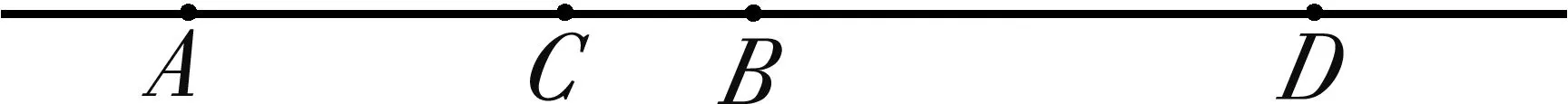
图4

A

B

C

D

C

D

A

B

A

B

C

D

3.3 调和线束及性质

如图5,从调和点列A,B,C,D所在直线外一点P,引射线PA,PB,PC,PD,则称线束PA,PB,PC,PD为调和线束.

图5

性质如图6,已知PA,PB,PC,PD为调和线束,若有一条直线l平行于其中的一条,且与剩余三条交于三点,那么这三点中的内点平分该线段.

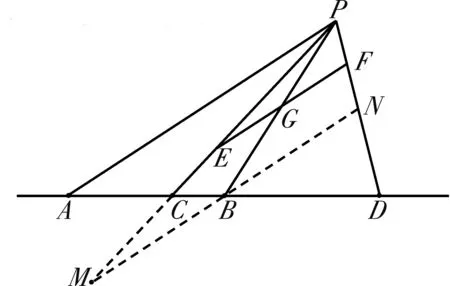
图6

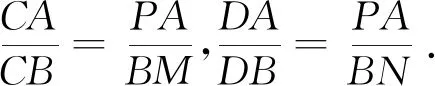
3.4 圆锥曲线中的调和点列

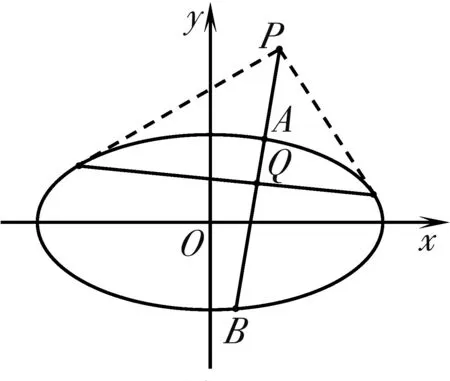
图7

4 试题拓展

我们来分析题1,2的命题背景.

题1背景如图8,设MN∩AB=Q,MT∩AN=V.首先注意到直线PA,PB均与椭圆相切,则直线AB为点P对应的极线,于是P,Q调和分割M,N,因此P,Q,M,N为调和点列,直线束AP,AQ,AM,AN为调和线束,由HV//AP可得,T为MV的中点,所以V和H重合,即NH过点A.

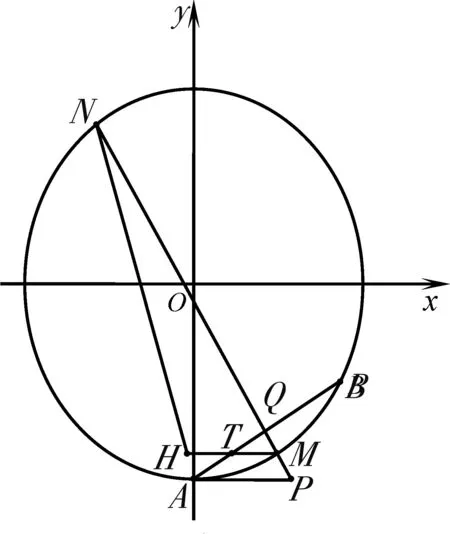
图8

题2背景如图9,点B对应的极线即为x=-2,设其与BN交于点H,可知B,H,M,N构成调和点列,因此AB,AH,AM,AN为调和线束,又PQ//AH,所以BP=BQ.

图9

由此可以命制以下试题:

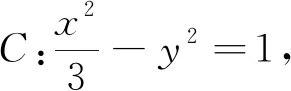
(1)求直线l倾斜角θ的取值范围;