浅谈函数中如何寻找同构解决“指对”问题
——2022年新高考Ⅰ卷第22题带来的思考
2023-04-15刘明明
刘明明
⦿江苏省南通市如东高级中学
全国高考数学卷中经常出现构造同构函数解决与函数有关的问题,尤其在处理“指对”问题时,通过同构函数往往能更好更快捷地解决问题.下面从2022年新高考Ⅰ卷第22题第(2)问出发,探索同构函数在解决“指对”问题中的应用.
1 原题呈现及分析
证明:存在直线y=b,其与两条曲线f(x)=ex-x,g(x)=x-lnx共有三个不同的交点,并且从左到右的三个交点的横坐标成等差数列.
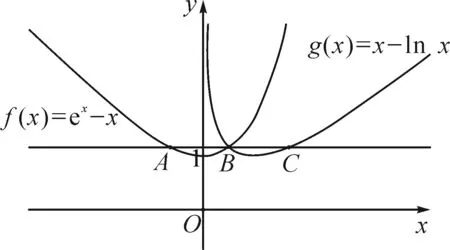
图1
分析:给出直线y=b,及两条曲线f(x)=ex-x,g(x)=x-lnx的图象,如图1所示.
不妨设三个交点的横坐标从左到右依次为x1,x2,x3,则有x1<0 由ex1-x1=eln x2-lnx2,知f(x1)=f(lnx2),又x1<0,lnx2<0,f(x)=ex-x在(-∞,0)上单调递减,故x1=lnx2;由ex2-x2=eln x3-lnx3,知f(x2)=f(lnx3),又x2>0,lnx3>0,f(x)=ex-x在(0,+∞)上单调递增,故x2=lnx3. 所以x1+x3=ex1+lnx3=eln x2+x2=2x2,原命题得证. 从上述分析可以看到,通过公式alogaN=N(N>0),logaaN=N(a>0,且a≠1),寻找方程中的相同结构,并利用函数f(x)=ex-x在(-∞,0),(0,+∞)的单调性,将复杂的“指对”等量关系式转化为简单的关于自变量的等量关系式.同时,我们不禁有这样一些思考:我们平时遇到的“指对”问题,是否同样可以通过同构函数加以解决?若能,则在“指对”问题中怎样才能找到同构函数呢?笔者通过以下几个方面来揭示运用“同构”思想处理“指对”问题的思维过程. 例1(2020年新课标Ⅱ卷第12题)若2x-2y<3-x-3-y,则( ). A.ln(y-x+1)>0 B.ln(y-x+1)<0 C.ln|x-y|>0 D.ln|x-y|<0 解:由2x-2y<3-x-3-y移项变形为2x-3-x<2y-3-y.令f(x)=2x-3-x,则原不等式即为f(x) 例1主要揭示了同构函数法不仅能应用于方程问题中,在不等式问题中也有广泛的运用,通过移项变形在等号(或不等号)两边分别构造同构形式,从而帮助我们更快捷地解决方程或不等式问题.如果遇到较复杂的含参恒成立问题呢?如例2. 例2(2020年新课标山东卷)已知函数f(x)=aex-1-lnx+lna.若f(x)≥1,求a的取值范围. 解法1:利用指数对数的运算可将f(x)=aex-1-lnx+lna=eln a+x-1-lnx+lna≥1等价转化为 eln a+x-1+lna+x-1≥lnx+x=eln x+lnx. ① 令g(x)=ex+x,则不等式①可等价转化为g(lna+x-1)≥g(lnx).显然g(x)为单调增函数,则不等式①进一步等价转化为lna≥lnx-x+1. 令h(x)=lnx-x+1,利用导数求得h(x)max=h(1)=0,则lna≥0,即a≥1. 所以a的取值范围为[1,+∞). 在例2的同构转化过程中,恒成立问题中的参数尽量放在同一函数的不同位置或不同函数的相同位置.当然例2的转化并不唯一,还可以如下处理. 所以a的取值范围为[1,+∞). 通过解法1与解法2可以看到为解决问题构造的同构函数并不唯一,而且例2还可以构造y=xlnx,y=x+lnx等同构函数来解决问题.但对比这些不同的同构函数,我们发现利用g(x)=ex+x处理问题更简洁方便,主要原因是相对于其他同构函数,g(x)的单调区间(-∞,+∞)最长,这样就不必对自变量是否在单调区间内加以讨论,故构造同构函数解决问题时,我们应尽量选择单调区间较长的函数. 例3(2020年新课标Ⅰ卷第12题)若2a+log2a=4b+2log4b,则( ). A.a>2bB.a<2b C.a>b2D.a 解:因为4b+2log4b=22b+log2(2b)-1,所以2a+log2a=22b+log2(2b)-1. 于是2a+log2a<22b+log2(2b). 设f(x)=2x+log2x,则有f(a) 对于例3,主要是利用放缩法将方程转化为两边可以构造同构函数的不等式形式,再由同构函数的单调性判断自变量的大小.类似的方法在证明含参不等式中也有着广泛的应用,如以下例4. ② 故当ln(ex)≤0时,②式显然成立.当ln(ex)≥0时,令g(x)=xex.由g′(x)=ex(x+1),知g(x)在(0,+∞)上增函数,又易证x≥ln(ex)=lnx+1,所以g(x)≥g(ln(ex)),即xex≥eln(ex)ln(ex)成立,亦即②式成立. 上述例3与例4都采用了放缩法寻找不等式两边的同构形式.有些问题中还可以利用一些常见不等式(如ex≥x+1)进行放缩,比如例5. 例5已知函数f(x)=x(e2x-a),若x>0时,f(x)≥1+x+lnx恒成立,求实数a的取值范围. 例5通过e2x+ln x≥2x+lnx+1的放缩,达成了分式的分子分母同构,巧妙得到不等式右边的最小值,极大地优化了本题的解题步骤. 这些类同构问题的解决过程也告诉我们:在平时的解题中,不能思维僵化,要多从范围、常见不等式等角度思考可否化为同构问题解决. 易知g(t)≥g(e2)=e2-2e2+e2=0.又0 所以0 例7(2013年新课标Ⅱ卷)已知函数f(x)=ex-ln(x+m),当m≤2时,证明f(x)>0. 证明:令g(x)=ex-x-1,则要证f(x)>0成立,即证g(x)+g(ln(x+m))+2-m>0成立. 又g(x)≥0,g(ln(x+m))≥0,当且仅当x=0且m=1时,上述两个不等式的等号同时成立.又m≤2,所以2-m≥0,当m=2时,等号成立.即上述3个等号不能同时取到.于是f(x)>0. 故原命题得证. 例7中的局部同构与例6有所不同,它寻找的不是自变量的局部同构,而是通过常用母函数f(x)=ex-x-1寻找整个函数的局部同构(形如f(x1)+f(x2)+m).这里如果先对例7的参数进行放缩,会更容易寻找到例7的局部同构.如以下另一角度. 另一角度:令g(x)=ex-x-1,要证m≤2时,f(x)>0,只需证ex-ln(x+2)>0,即证g(x)+g(ln(x+2))>0.又由g(x)≥0,g(ln(x+2))≥0,当且仅当x=0且x=-1时,两个等号同时成立.又等号取不到,故原命题得证. 从以上的思考角度我们可以看到,这三种类型同构问题并不是孤立的,而是相互联系的,在解决“指对”问题时需要灵活加以运用. 最后,大数据显示“指对”问题在全国卷中的出现非常频繁,而构造同构函数的思想在解决“指对”问题时也越来越重要,因此在平时的教学中要向学生多渗透,让他们在解决“指对”问题时更加游刃有余.2 “同构”思想处理“指对”问题的思维过程
2.1 在等号(或不等号)两边分别构造同构函数
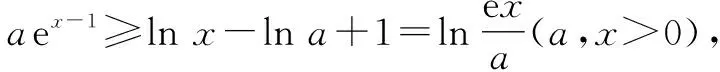
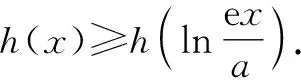
2.2 利用放缩构造不等式中的同构函数


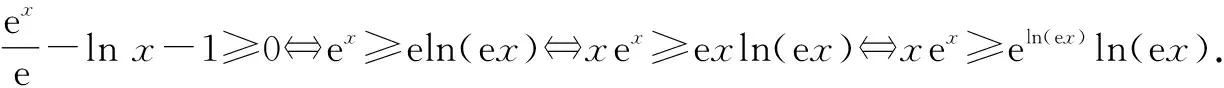

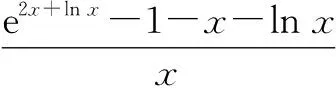
2.3寻找方程、不等式中的局部同构