一道向量题的探究

王惠清

⦿江苏省南通市通州区教师发展中心

平面向量问题一直是每年模拟、高考、竞赛等考试中的热点与重点问题之一，其借助平面几何的背景，创新性、新颖性皆很强，且变化多端，常考常新，同时也是数学知识交汇与融合的理想场所之一，是考试中能力齐全、思维各异、方法多样的一个主战场.破解平面向量问题，主要是抓住平面向量与平面几何的图形特征，借助基底思维、坐标思维、解三角形思维等方式切入，结合平面向量的相关运算，得以研究相关的几何元素之间的关系问题.

1 问题呈现

问题(2020届湖北省武汉市武昌区高三年级4月调研测试数学理科试卷·10)如图1所示，在由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形中，设DF=3FA，则( ).

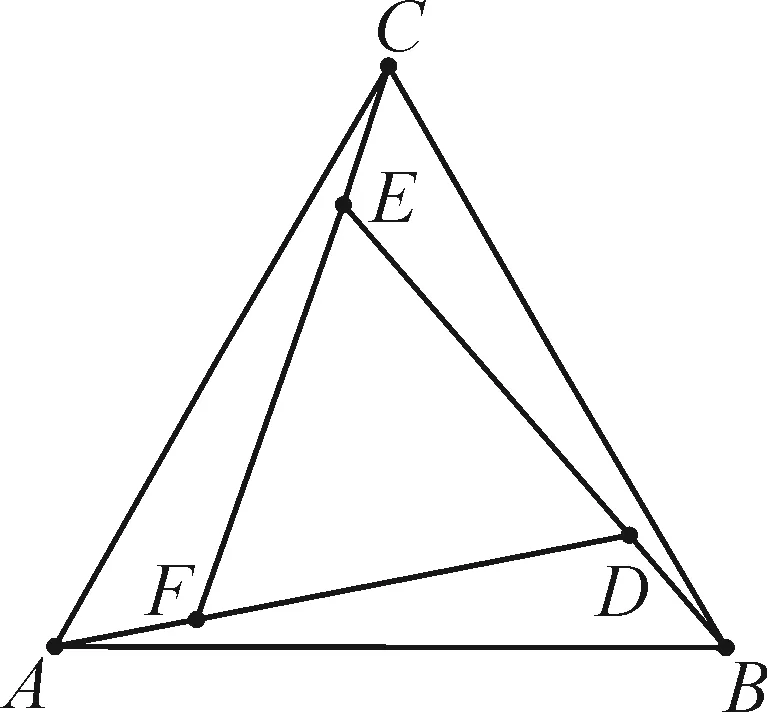
图1

此题设计新颖别致，题意简洁明了，目标明确，立意深刻，通过平面几何图形的拼接与组合，以两个具有特殊关系的等边三角形为问题背景，结合其中线段之间的比例关系来确定平面向量的线性关系式.问题以平面几何图形为背景，使得命题条件独具特色，并增加了思维难度，充分体现了新课标高考的“多考思维，少考计算”的命题新理念，意在考查学生的观察、归纳、猜想和逻辑推理以及数学运算能力.

2 问题破解

思维视角一：基底思维

方法1：基底法——线性运算法.

解析：根据题目条件可知△ABD≌△BCE≌△CAF.

由DF=3FA，可得ED=3DB，FE=3EC.

点评：根据平面图形的形象直观性，数形结合，利用三角形法则，结合平面向量的线性运算加以转化，“一条路到底”，再结合基底法的应用来确定平面向量的线性关系式，从而正确求解.

方法2：基底法——待定系数法.

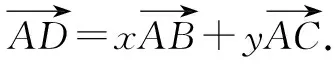
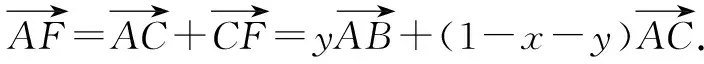
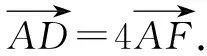
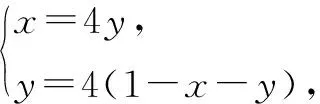
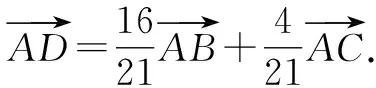
思维视角二：坐标思维

方法3：坐标法.

解析：以A为坐标原点，AB所在直线为x轴建立平面直角坐标系，如图2所示.

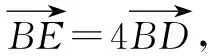
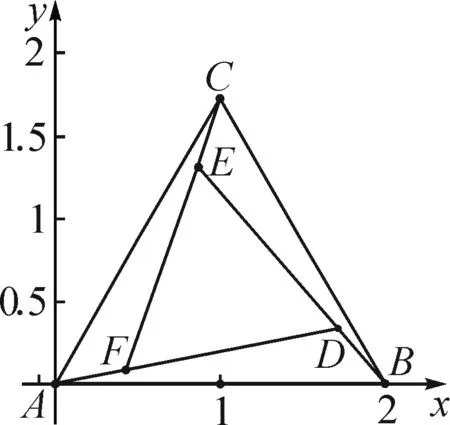
图2

E(16x-6，16y).

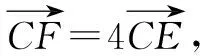
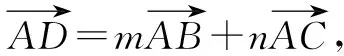
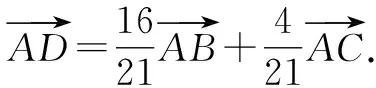
点评：根据条件建立平面直角坐标系，设出点B的坐标，从而确定点C的坐标.设F(x，y)，利用条件中线段长度的关系分别表示出点D，E的坐标.结合CF=4CE建立相关参数的方程组，进而确定点D的坐标.利用平面向量的基本原理及其坐标运算建立关系式，结合待定系数法来求解相应的参数值，从而正确求解.

思维视角三：解三角形思维

方法4：余弦定理法.

图3

解析：如图3所示，延长AD交BC于点M，延长BE交CA于点N.

结合DF=3FA，根据对称性，可设AF=BD=CE=1，DF=ED=FE=3，BM=CN=x，DM=EN=y.

在△BCE中，由余弦定理，得

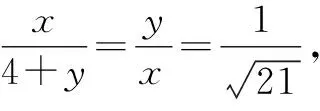
点评：根据条件构造相应的辅助线，通过设出相应的线段长度，并结合余弦定理的应用确定BC的长度.通过相似三角形的判定与性质建立相应的关系式，得以确定相应的参数值，再结合平面向量的平行关系、共线性质以及线性运算进行分解，从而正确求解.

方法5：正弦定理法.

解析：如图4所示，延长AD交BC于点M.

图4

结合DF=3FA，根据对称性，可设AF=BD=CE=1，DF=ED=FE=3.记∠DAB=α，∠DBA=β.

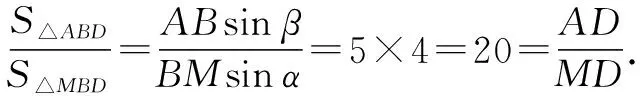
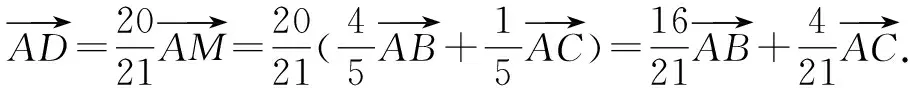
点评：根据条件构造相应的辅助线，通过设出相应的线段长度，并结合正弦定理的应用确定线段之间的关系，再结合三角形面积之间的关系加以转化与应用，进而确定线段之间的比例关系，最后结合平面向量的平行关系、共线性质以及线性运算进行分解，从而正确求解.

3 变式拓展

探究1：保留题目条件，根据大、小等边三角形之间的比例关系，通过面积关系来设置几何概型问题，利用概率的求解来进行合理变式.

变式1如图1所示，在由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形中，设DF=3FA，若在大等边三角形中随机取一点，则该点取自小等边三角形内的概率是.

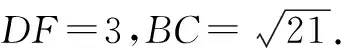
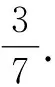
探究2：保留原问题的部分条件，把具体的线段比例关系进行一般化处理，将原问题变式拓展，从而得到相应的一般性结论.

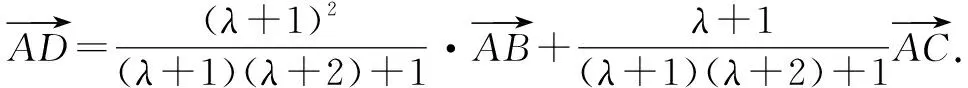
该结论的具体证明过程可参照原问题中方法4的求解过程.利用该结论，可以确定小等边三角形与大等边三角形边长的关系、面积的关系以及与之相关的其他问题，包括变式1中的几何概型问题等.

4 解后反思

破解平面向量问题最常见的“三思维”：基底思维、坐标思维、解三角形思维.在实际解答过程中，利用平面向量的线性运算或坐标运算来分析与处理，具体破解与切入方式又有不同的形式.其实，在解决平面向量问题时，要充分利用平面向量的特征，提高识“图”与用“图”能力，提升用“数”与解“数”思维，进而从“形”的角度或“数”的角度切入，结合不同的思维方式来分析，达到多角度思维，多方法处理，多层面拓展.