多题一解，培养运算素养——齐次化在2022年高考圆锥曲线题中的应用

崔 征

⦿湖北省宜昌市葛洲坝中学

夏咏芳

⦿湖北省宜昌市夷陵中学

圆锥曲线的相关问题是高考数学考查的一个热点，这类问题的特点是计算量较大，平时的复习备考不仅要掌握常规方法和基本技能技巧，还要注意归纳总结，对于特定的问题，还要学习一些特定的方法.如果题目中出现两直线斜率之和或者之积的条件时，常常可以利用齐次化的方法大大降低计算量.接下来我们一起看看2022年的几道高考题是如何用齐次化的方法简化计算的.

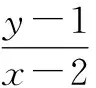
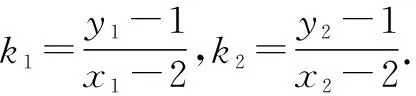
[(x-2)+2]2-2[(y-1)+1]2=2.

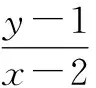
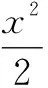
整理双曲线方程，得

[(x-2)+2]2-2[(y-1)+1]2=2，

即(x-2)2+4(x-2)-2(y-1)2-4(y-1)=0.

将双曲线与直线方程联立，构造齐次式得

(x-2)2+4(x-2)[m(x-2)+n(y-1)]-2×(y-1)2-4(y-1)[m(x-2)+n(y-1)]=0，

两边同时除以(x-2)2，可得

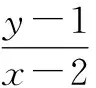
(-2-4n)k2+(4n-4m)k+1+4m=0.

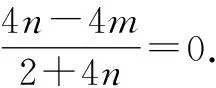
解得n=m，代入直线l，可得l的斜率为-1.

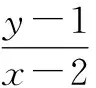
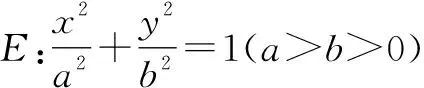
(1)求椭圆E的方程；

(2)过点P(-2,1)作斜率为k的直线与椭圆E交于不同的两点B,C，直线AB,AC分别与x轴交于M,N，当|MN|=2时，求k的值.

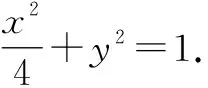
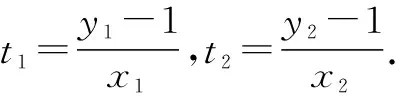
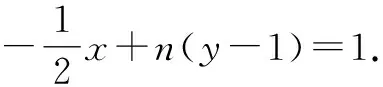
椭圆方程可变形为x2+4[(y-1)+1]2=4，展开得x2+4(y-1)2+8(y-1)=0，齐次化，可得

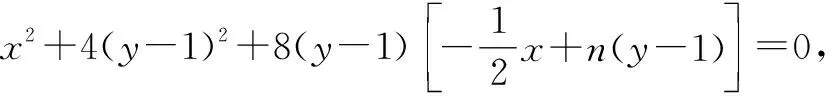
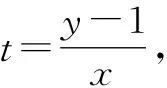
由Δ=-32n>0，得n<0.

直线lAB方程为y=t1x+1，直线lAC方程为y=t2x+1，则两直线与x轴的交点分别为

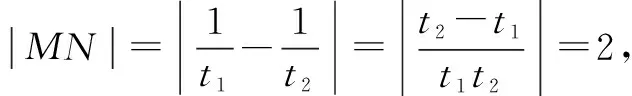
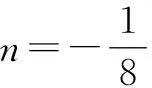
点评：该题第(2)问的主要线索是|MN|=2，我们可以把|MN|的长度用AB,AC的斜率表示出来，但凡碰到有斜率之和或者斜率之积，或者斜率之差，都可以用这种齐次化的方式来简化计算.

图1

(1)求点P到椭圆上点的距离的最大值；

(2)求|CD|的最小值.

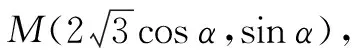
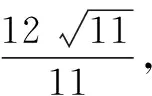
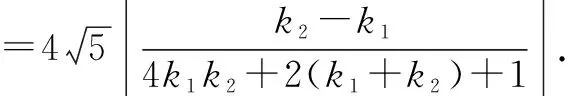
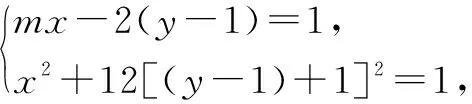
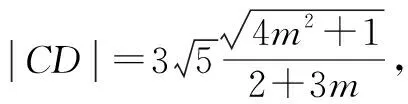
其实不仅在2022年的高考中，齐次化能发挥重大作用，在往年的高考中不少圆锥曲线问题都可以用齐次化大大地简化运算，比如2020年山东卷中解析几何大题也可以用齐次化法简化计算，读者朋友不妨尝试一下.关于齐次化，大家还需要注意一下几点：

(1)如果圆锥曲线的题目里出现斜率之和或者斜率之积，或者斜率之差等条件，那么就可以尝试用齐次化来解决.

(2)如果直线经过的点在曲线外，曲线与直线联立后往往不仅会剩下一次项，还会剩下常数项，这个时候也可以秉承齐次化的思想加以处理，将1平方就可以构造出二次项了.

(3)齐次化的方法不仅可以解决与椭圆有关的定点定值问题，同样也适用于双曲线和抛物线，在这里就不做过多的赘述了.