目标意识在数学解题教学中的培养策略*

刘远来 李红梅

⦿西华师范大学

目标意识是指一种由主体依据解题目标，分析条件和作用、结论和等价关系，有目的地将条件和结论相关联的思维活动.其中解题目标可分为中间目标和最终目标.目标意识的培养有助于学生明确解题方向，探寻解题切入点，构建解题系统.

著名数学家波利亚在《怎样解题》中说：我们喜欢朝着目标直接走，对于绕着走、反着走、或者脱离目标有一种心理上的反感.由此可见目标意识的重要性，目标意识对于解题起着导向性作用.而现在中学生由于思维水平、认知结构的局限性，在难题的处理上缺乏目标意识，找不到破题口.基于在解题教学中如何引导学生解题，培养学生核心素养，避免学生在解题过程中的盲目性，笔者从目标意识入手，从以下三个方面浅谈目标意识的培养策略.

1 活用化归思想，明确解题方向

化归思想是指复杂问题通过某种变换转化为简单问题，未知问题转化为己知问题的过程，达到化生为熟，化难为易，化繁为简，化迂为直的目的.运用化归思想，对题目的解题目标进行变换，明确解题的方向，增强学生解题的目标意识，在化归中培养学生创新性思维.

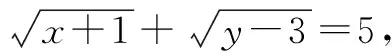
分析：这是一道根据等式限制条件求取值范围的题目，如果运用常规思路用一个变元表示另一个变元，计算过程较为复杂，也不易求解.下面利用化归思想架构知识之间的联系，变换解题目标，明确解题方向.

根据化高维为低维的划归思想，采用换元法进行化归：

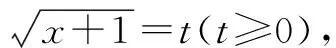
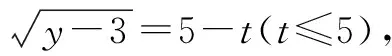
所以2x+y=2(t2-1)+(5-t)2+3

=3t2-10t+26(0≤t≤5).

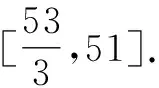
2 借助逆向思维，探寻解题切入点

逆向思维是一种思想(概念、原理、观念)反过来思考的思维方式.具体而言，是把题目中的结论当作条件，并结合题设部分条件，通过转化、推理，得到一个显而易见的结论.通过这种思维方式得到的结论就是探寻解题切入点的关键.逆向思维不仅在利用定义、运算法则、定理进行解题时经常使用，而且对于几何、不等式和导数的相关证明也有妙用.

例2若a,b,c是不全相等的正数，求证：

分析：该题是一道证明不等式恒成立的问题，但是利用显性题设条件很难证明结论，不易探寻解题的目标切入点.下面通过逆向思维来分析试题，并展现目标意识的思维过程.

3 巧用概念图，构建解题系统

概念图是组织知识和表征知识的工具，包括概念或命题间的相互关系，概念通常置于圆圈或方框中，用连线及其连接语表明两概念间的联系.

对于一个初始条件复杂、结论较为抽象的问题，我们往往难以入手，目标迷茫，想不到破题的关键.我们不妨引入概念图厘清条件和结论之间的关系，构建解题的层级目标，形成解题的目标系统.绘制数学概念图，有利于提高学生发现问题、提出问题、分析问题、解决问题的能力，有利于培养学生逻辑推理和直观想象核心素养，有利于提高学生思维的系统性、广阔性、深刻性，为数学解题目标意识的培养提供了一种思维工具.

构建概念图的流程如下.首先，将解题的结论作为最终目标；其次，分析题目中每个条件的作用及其相互关联关系；然后内化条件，相互转化，推理出所需的中间目标，并用箭头进行有意义连接，标注好两个目标之间的关系；再次，厘清各个过渡目标的内外层级、因果关系，形成一个完整、逻辑清晰的概念图；最后，对所构建的概念图反思每个过渡目标的确定是否合理、正确，每个目标之间的意义连接是否有用.

例3已知函数f′(x)是奇函数f(x)(x∈R)的导函数，当x<0时,xf′(x)+f(x)>0,且满足f(-2)=0,则使f(x)>0成立的x取值范围是( ).

A.(-∞,-2)∪(0,2) B.(-2,0)∪(2,+∞)

C.(-∞,-2)∪(2,+∞) D.(-2,2)

根据例3题设条件，绘制概念图需要确定以下几个中间目标.

目标一：这是一道结合导数知识的不等式抽象函数问题，这类问题的解题策略是什么？

在数学解题中注重通性通法.这类问题的解题策略往往是利用函数单调性脱去“f”的方法，将抽象函数不等式转化为具体函数不等式，进而利用不等式性质求出未知数的取值范围.因此，这是我们解题的总体目标，为解题确定了方向.

目标二：根据条件x<0,xf′(x)+f(x)>0,我们可以关联到哪些知识点，对解题有何作用？

可以联想到函数F(x)=xf(x)的导函数为F′(x)=xf′(x)+f(x),利用逆向思维构造函数F(x)=xf(x)，那么导函数的单调性迎刃而解.在此过程中xf′(x)+f(x)>0,决定了导函数的正负性，进而确定了F(x)的单调性，是解题的关键之处.

目标三：根据条件“函数f′(x)是奇函数f(x)(x∈R)的导函数”，从函数的奇偶性考虑，F(x)与f(x)有什么关系？在探寻解题目标的过程中有何作用？

f(x)的奇偶性决定了F(x)的奇偶性，F(-x)=-xf(-x)=xf(x)=F(x),因而F(x)是偶函数.而目标二只能确定(-∞,0)上函数图象的变化趋势，当确定了F(x)是偶函数，(0,+∞)上的函数图象变化趋势便一目了然.

目标四：条件f(-2)=0的作用是什么？

作用有三：其一是确定了构造的函数的零点，分割清楚函数值的正负范围；其二是得到了f(2)=0；其三是为了将f(x)>0等价变形为f(x)>f(-2)，或f(x)>f(2).

目标五：如何由F(x)>0来确定f(x)>0的取值范围？

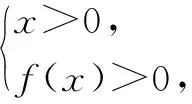
由上述确定的五个中间目标绘制如图1所示的概念图.

图1

问题是数学的心脏，数学问题的解决是培养学生数学核心素养的重要成分.由上述分析可知目标意识在解题中发挥着举足轻重的作用.加强学生解题的目标意识，从多角度、多途径进行培养，并考虑学生自身情况，因材施教.这样,学生在解题时才能做到积极思考和主动探究，提高数学解题能力，抓住数学本质,引导学生会用数学的思维思考现实世界.