一道高考多选题的深度教学与思考*

刘 娟

⦿合肥市第一中学合肥市刘娟教育名师工作室

自2020年起，全国高考数学新课标Ⅰ卷以《普通高中数学课程标准(2017年版)》和《中国高考评价体系》为依据，试卷不分文理科，由八道单项选择题、四道多项选择题、四道填空题和六道必做解答题组成.其中，多项选择题是新的类型，每小题5分，部分选对得2分，有选错得0分，即见错归零，减少单选题中通过盲选也可得满分的可能性，有效提高了满分的思维价值.多选题的构成要素较复杂，破解难度大，需要的能力点多，依托数学模型，强调对数学思想方法的考查，要求学生具有完备、细致、全面的思维品质[1].多选题四题中前两题较为基础，后两题难度较大.

笔者以2021年新课标Ⅰ卷第12题为例，分析问题并从深度学习的不同角度给出教学建议.

1 问题呈现

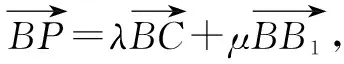
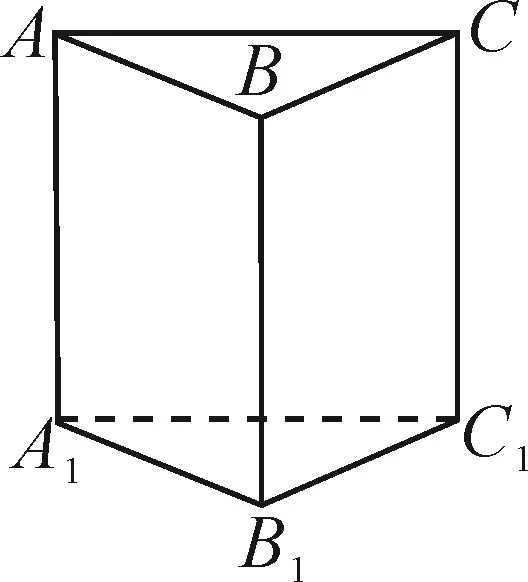
图1

A.当λ=1时，△AB1P的周长为定值

B.当μ=1时，三棱锥P-A1BC的体积为定值

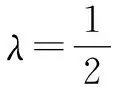
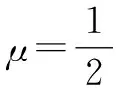
2 问题破解

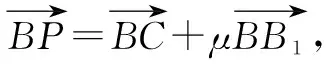
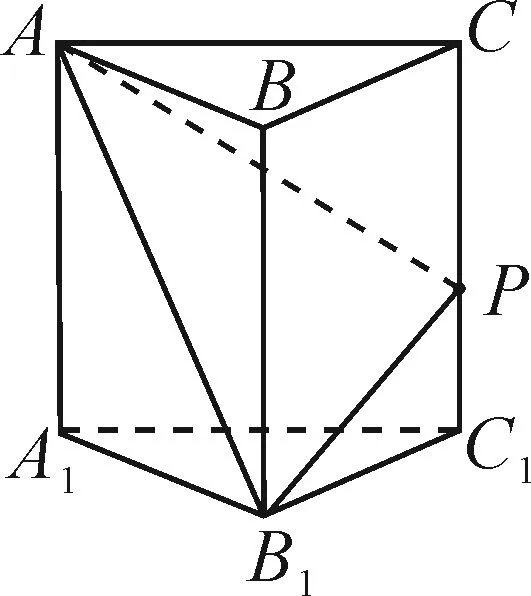
图2

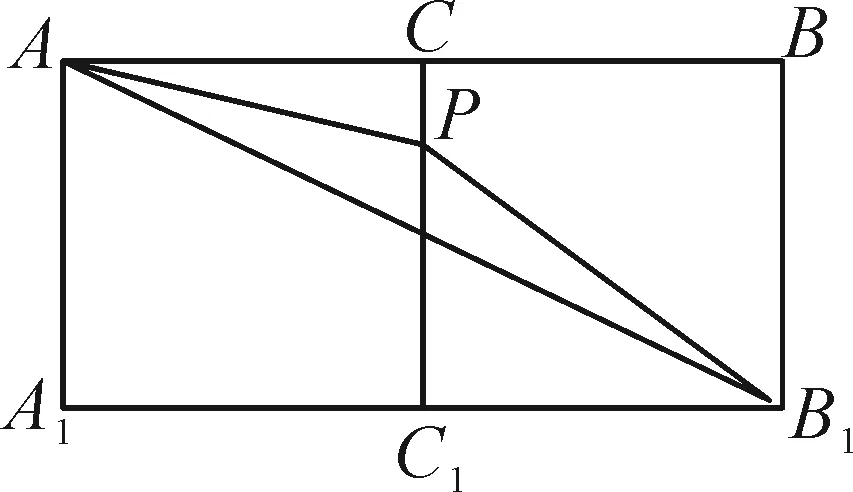
图3

法1：计算点P分别在线段CC1的端点C，C1及在线段CC1中点处时△AB1P的周长，对应的△AB1P的周长不相等，从而△AB1P的周长不是定值，故排除A选项.

法2：如图3，将面AA1C1C与面BCC1B1展开成长方形AA1B1B，连结AB1，由于点P在线段CC1上运动，显然△AB1P的周长不是定值.

法3：要判断△AB1P的周长是否为定值，只需判断|B1P|+|PA|是否为定值.

设|PC1|=x，x∈[0，1]，则

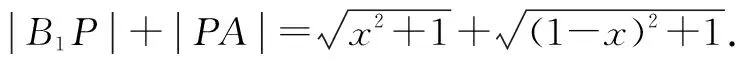
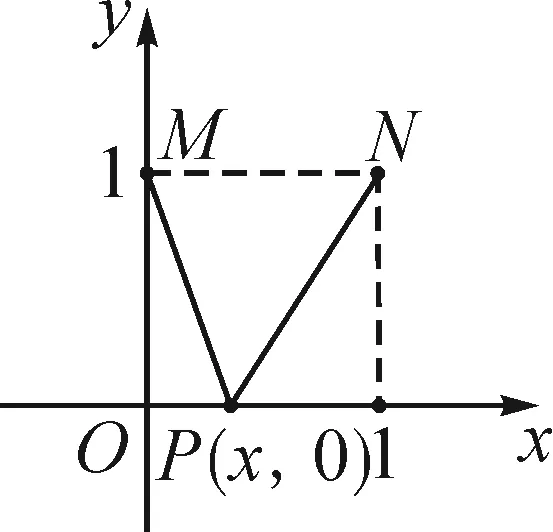
图4

图5

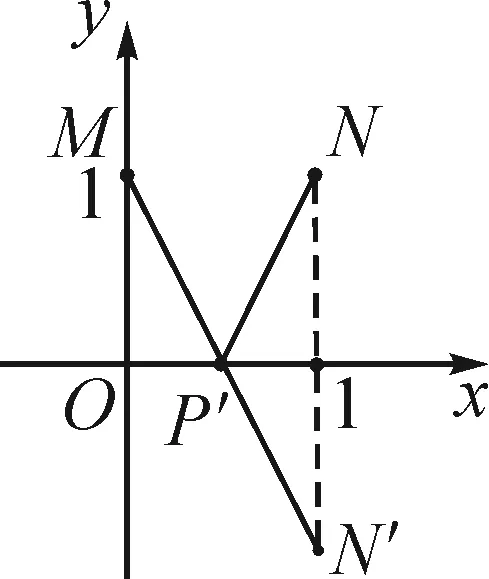
图6

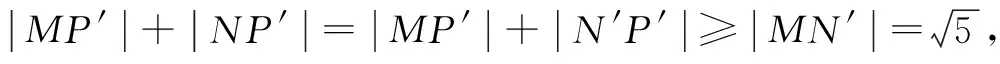
图7

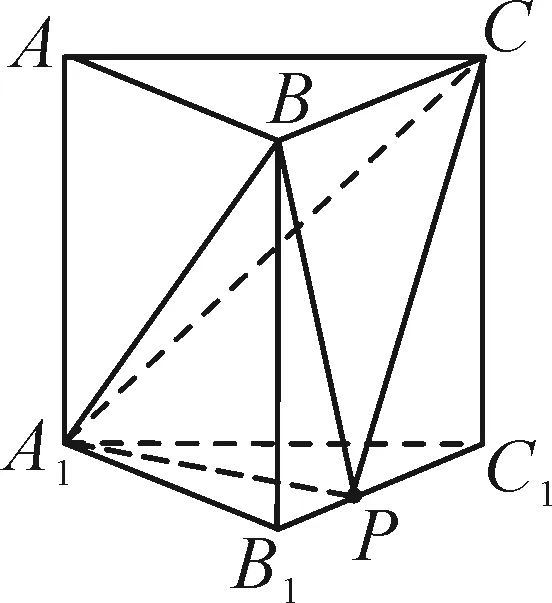
图8

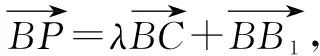
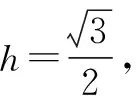
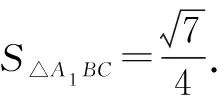
图9

图10

图11

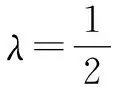
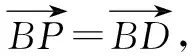
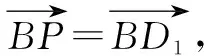
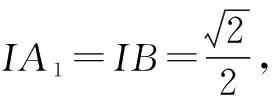
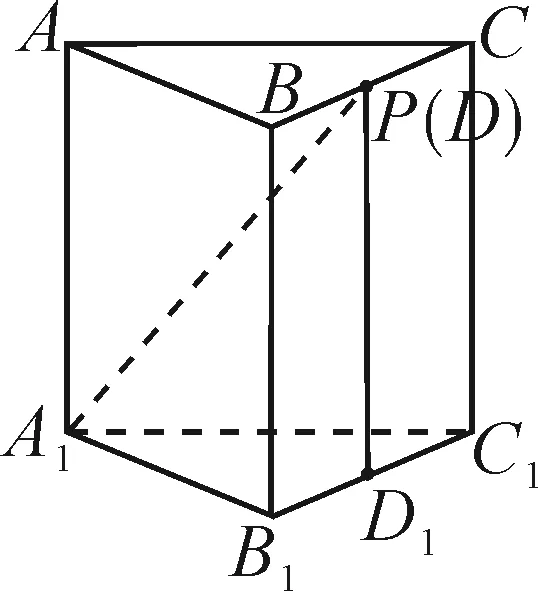
图12

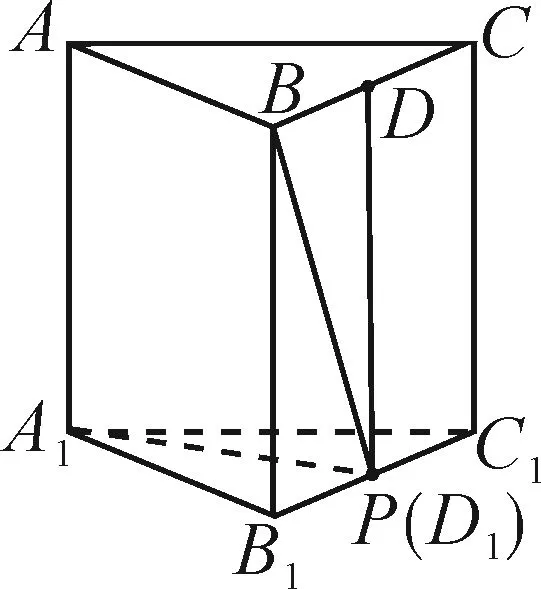
图13

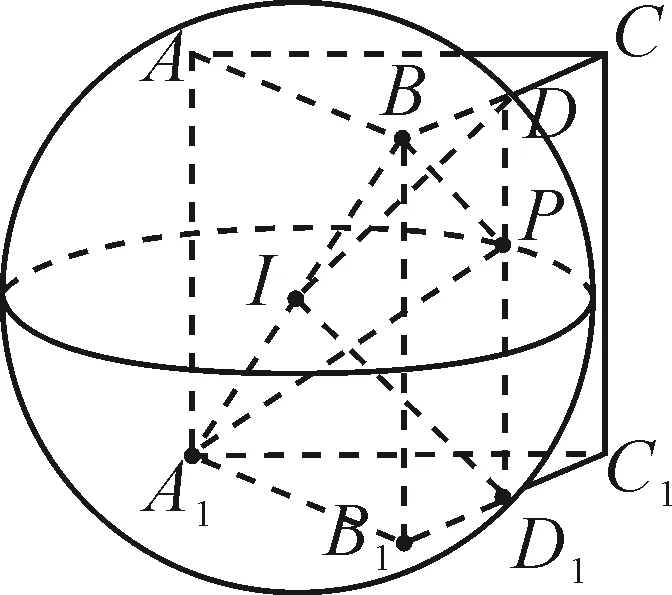
图14

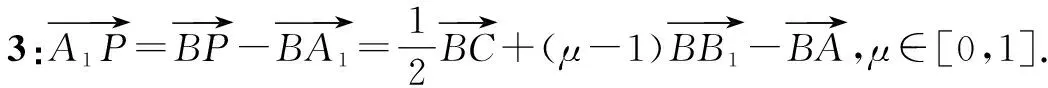
所以μ=0或μ=1.故点P不唯一.

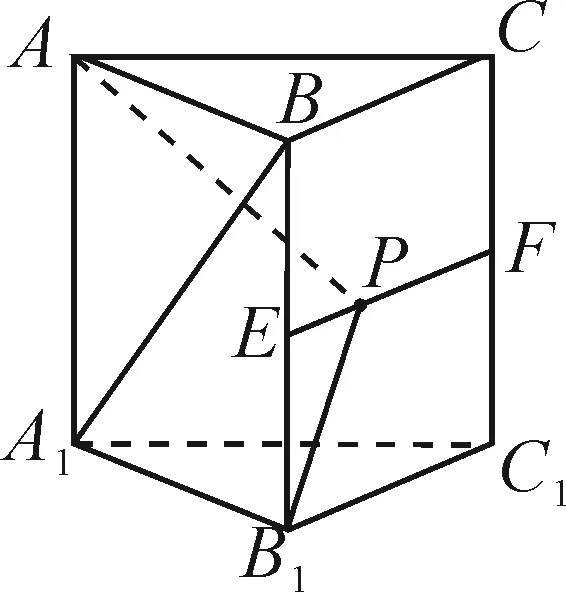
图15

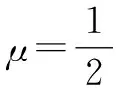
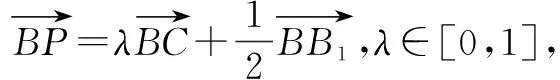
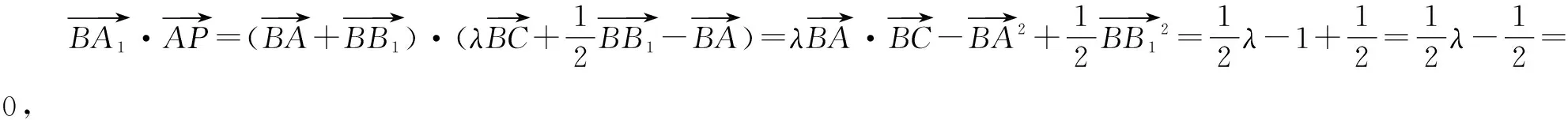
故有且只有一个点P满足条件.

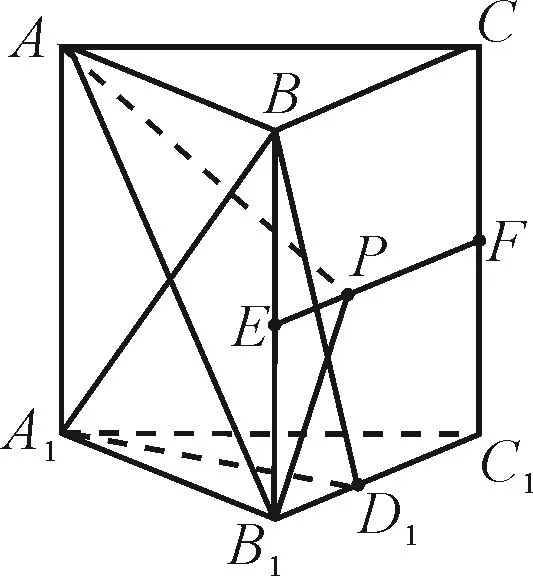
图16

法2：要证A1B⊥平面AB1P，只需证明A1B垂直于平面AB1P内的两条相交直线.由于ABC-A1B1C1是正三棱柱，显然A1B⊥AB1.问题转化为“判断满足A1B⊥B1P的点P是否唯一”.点A1在平面BCC1B1内的投影为B1C1的中点D1(如图16)，要想得出A1B⊥B1P，只需证BD1⊥B1P成立即可.显然只有当点P运动到点F时，△BB1D1≌△B1C1F，易得BD1⊥B1P，从而A1B⊥B1P.因此有且仅有一个点P，使得A1B⊥平面AB1P.故选项D正确.

研究图形的基本思想方法有综合几何法、解析几何法、向量几何法和分析法.在上述讨论中，显然向量几何法在位置关系的判断上比较简洁，后两个选项直接利用平面向量的数量积便可做出判断，但在度量关系上并不一定占据优势，所以前两个选项重点用综合几何法和分析法进行判断.本题还可以通过建立空间直角坐标系，使用空间向量的坐标运算来研究图形，具体解法交由读者自行研究.

3 教学建议

3.1 关注研究内容的结构与联想

本题对图形的基本性质(如图17所示)的考查全面且深入.题干运用平面向量基本定理表述点的位置，利用系数的变换，点动成线，用平面的表述方式实现空间位置的确定，体现了立体几何教学中常用的将三维空间几何问题转化为二维平面中的问题来解决的基本思想.《普通高中数学课程标准(2017年版2020修订)》对整体的课程架构归纳为整体→局部→整体，其中运动变化观点是几何课程的主线之一，而从变化中抓住不变的本质是教学的重难点.关注学生的思维过程，讲解的思维进阶要符合学生的认知规律.随着内容的递进，以立体几何为主体，不断聚合不同主题下的相关知识点，抽丝剥茧，再重新织成网，以此为触发器带动学生由被动学习到学会思考、学会迁移.

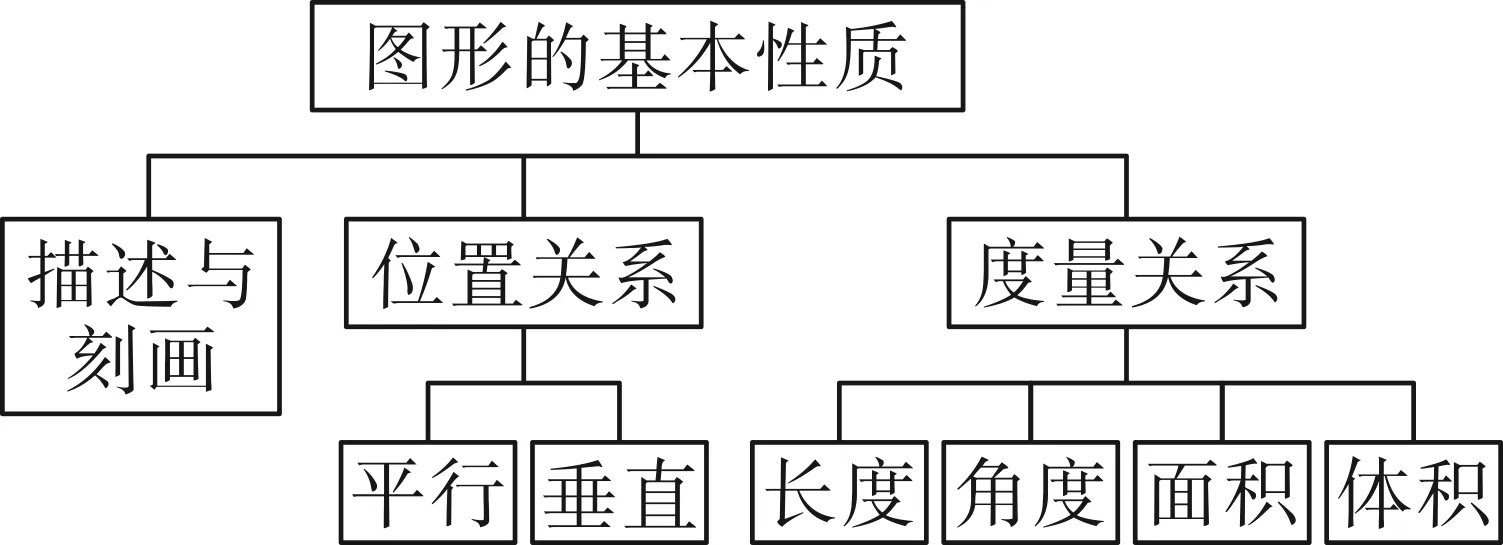
图17

3.2 拓展轨迹形式，内化知识的本质

本题四个选项得出的点P的轨迹仅为与三棱柱的棱平行或垂直的线段，还可以作出以下变式，可不拘泥于题中λ，μ的范围.本质与变式强调的是学生对教学内容的内化[2].

变式1点P的轨迹为在三棱柱侧面或底面上的线段.

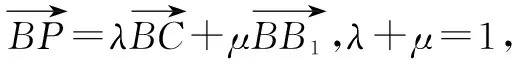
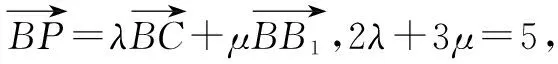
变式2点P的轨迹为在三棱柱侧面或底面上的曲线.

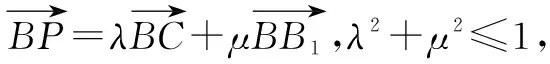
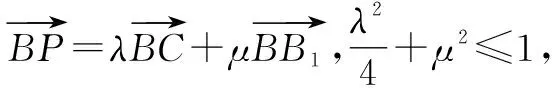
变式3点P的轨迹为在三棱柱内的平面或曲面.

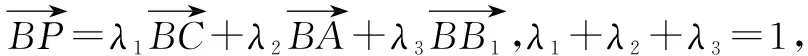
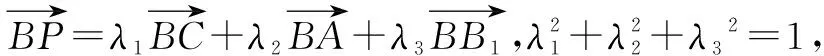
3.3 重要特征一般化，实现知识的迁移

以正三棱柱为载体体现了新高考考查主干内容的基础性，强调了利用模型解题的通性通法，也可以回归到最基本的正方体中，还可以在夯实点线面位置关系的同时强化度量关系，尤其是本例中未强调的角度问题，也可以通过割补等方式，引入陌生几何体，或者加强对生活实践的考查，以现有建筑或生活用品呈现的几何体为例抽象出空间图形，以生考熟.

学会应用是迁移的重要表征，也是检验学习效果的最佳途径.迁移与应用强调的是学生对学习成果的外化.如果把学习过程看作一个闭环结构，那么迁移发生在闭合处，从别处迁移来，又从这里迁移到别处[2].

4 深度学习的发生

深度学习具有在学习对象(内容)上关注联想与结构、本质与变式，在学习机制中关注活动与体验、在学习实践中关注迁移与应用，以及关注学生核心素养发展的价值与评价等特征[3].

高考立足于立德树人根本目标，目前是新课标、新课程、新教材与新高考的交汇时期，如何以核心知识的讲授、核心素养的培养为不变，应命题方式、试卷结构及题目类型等的万变，教师需要思考并尝试，坚持结合学生的切身实际，持续改进教学.研究高中数学深度学习后发现，思维的深度很多时候体现在数学思想方法的运用上，当学生能够结合数学思想方法建立起能迁移且具有批判精神的思维方式时，深度学习就能够成为发生在课堂中的真实景象[4].