源于教材 高于教材——“长短弦定理”及其推论

⦿山东省德州市临邑第一中学

刘文明 王志武

历年来，在高考、模考中，以过圆锥曲线焦点的弦为背景的问题(简称焦点弦问题)层出不穷，经久不衰.比如，2022年全国新高考Ⅰ卷第16题，2022年山东临沂一模第21题，2020年高考山东卷第13题，2018年新课标全国Ⅱ卷第19题，等等.很多专家学者也对焦点弦的性质进行了研究，但都用到了圆锥曲线的第二定义，如文献[1]、文献[2]等.由于2019年版新教材及更早的教材中已删减了圆锥曲线的第二定义，影响了相关性质和结论的推广和应用.为便于高中师生理解和接受，笔者避开第二定义，在横向椭圆的基础上利用高中知识对焦点弦的性质进行了研究，提出长短弦定理及相关推论.实践证明，长短弦定理及其推论是解决焦点弦长度问题的有力工具之一.

1 角度式焦半弦公式

为了叙述的方便，我们把过圆锥曲线焦点的弦称为焦点弦，焦点弦被焦点分成两部分，每一部分都称为焦半弦.

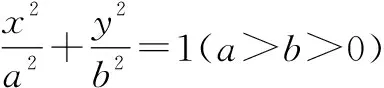
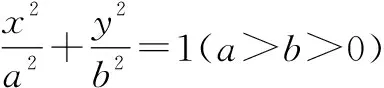
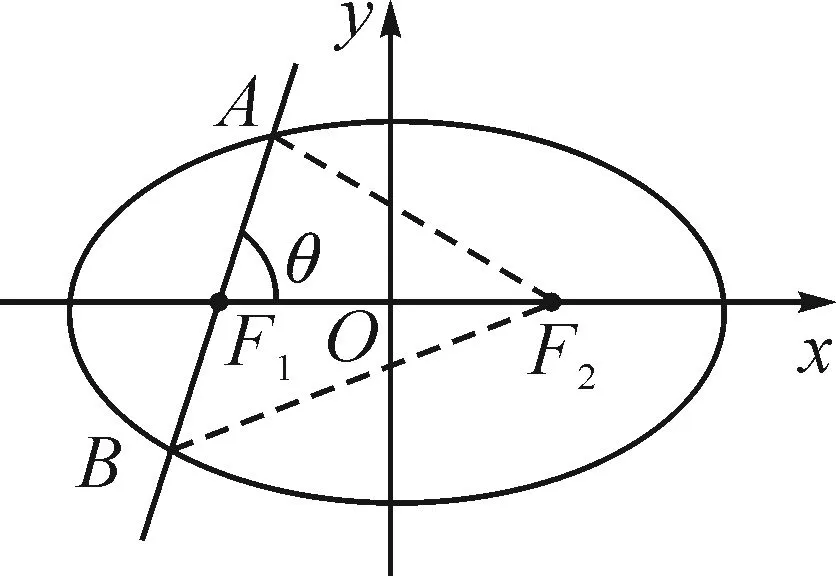
图1

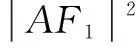
这个公式记忆的难点是分母中的正负号，其规律是上减下加.即对横向椭圆来讲，当弦AB过左焦点且点A在上方时，公式成立.

2 “长短弦定理”及其推论

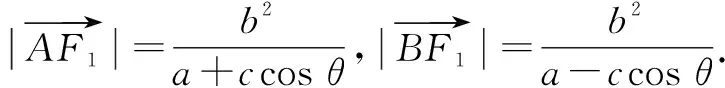
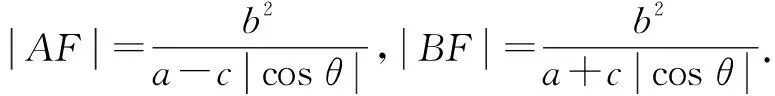
(注：这里a,b,c,p都是标准方程对应曲线的相关参数,以下同.)

由长短弦定理可进一步推演得如下推论成立.

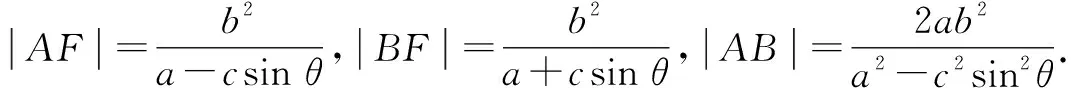
推论2证明从略.

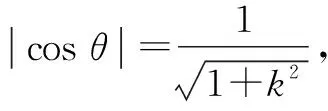
3 “长短弦定理”及其推论应用举例

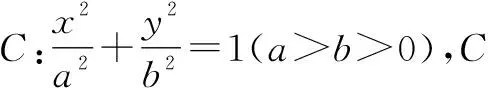
图2

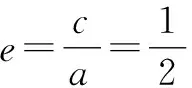
由“长短弦定理”，得

因为直线ED为线段AF2的垂直平分线，所以△ADE≌△F2DE,故△ADE的周长l=|DE|+|EF2|+|DF2|=4a=13.

分析：传统解法是先设出直线方程，与椭圆方程联立消元，然后利用弦长公式表示出弦长，再进一步求值，这样计算量大，冗长易错，容易陷入小题大做的陷阱.两种解法对比如下.

解法1：传统解法.

(3+4k2)x2-8k2x+4k2-12=0.

由弦长公式,得

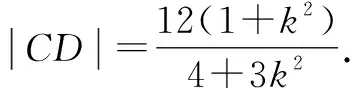
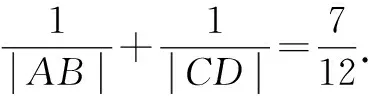
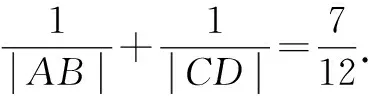
解法2：利用长短弦定理及其推论.

两种方法对比,解法2计算量小，简洁明快，节约时间.对于选择与填空题，优势明显.

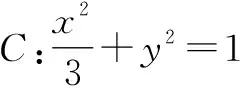
分析：本题的传统解法是设出直线BF1的方程，然后与椭圆方程联立消元，利用韦达定理及弦长公式、点到直线的距离公式等将四边形的面积表示出来，再研究最值，这样计算量大，繁琐易错.如图3所示，延长BF1交椭圆于点A1，由对称性可知|AF2|=|A1F1|,故AF2，BF1可以看作是同一焦点弦的两个焦半弦，可借助长短弦公式求解，事半功倍.

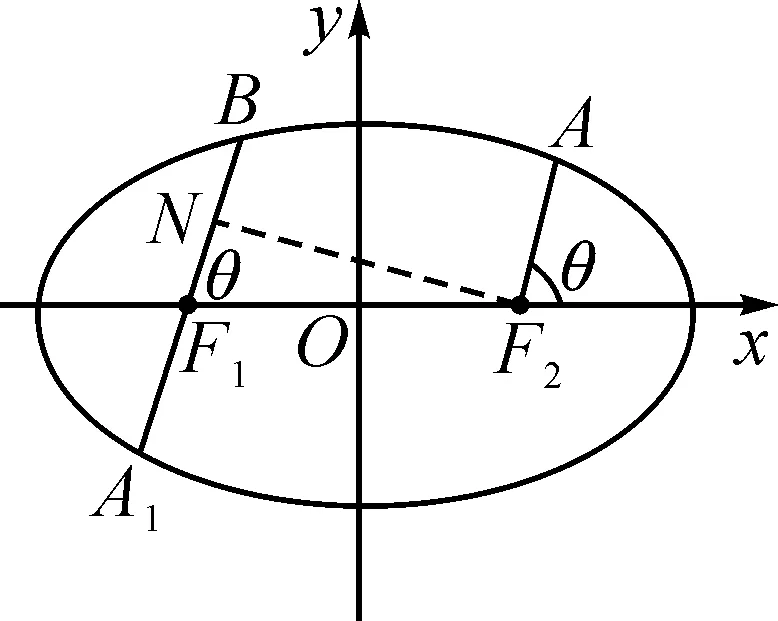
图3

例4(江西省新八校2019届高三第二次联考)如图4，过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A,B，交其准线于点C，若|BC|=4|BF|，且|AF|=6,则p的值为.

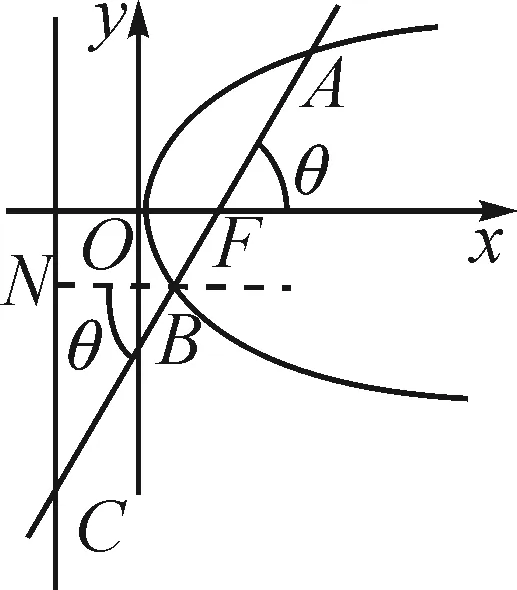
图4

统计往年试题发现，与焦点弦长度有关的问题在高考、模考中出现频率较高.高中阶段解决焦点弦问题的传统方法是将直线与曲线方程联立，消元后得到一元二次方程，然后利用韦达定理及弦长公式求解,其实质是代数法，运算量与思维量较大，求解过程繁琐耗时且易错.而用“长短弦定理”及其推论处理与焦点弦长度有关的问题，其实质是几何法，求解过程简洁明快，思维量与计算量小，准确率高.高中阶段适当拓展相关知识，有利于开拓学生思路，提高解题效率.