促进“思维生长”的初中生数学学习干预案例研究

[摘  要] 无论是从经验的角度来看，还是从理论的角度来看，要想促进学生的思维生长，最关键的就是要关注学生的学习过程. 对初中生的数学学习干预来说，当目的确定为学生思维生长时，就意味著思维生长应当成为初中生数学学习干预的落脚点. 评价学生思维生长的指标可以明确为学生的比较能力、推理能力、概括能力. 学生出错时就是学习干预时，此时干预往往容易让学生形成深刻印象.

[关键词] 思维生长;初中数学;学习干预;案例研究

基金项目：无锡市教育科学规划课题“促进‘思维生长’的初中生数学学习干预案例研究”（B/D2020/16）.

作者简介：周佳（1983—），本科学历，中学一级教师，从事初中数学教学工作.

任何一个学科的教学都不能忽视思维这样一个关键要素，只有学生在学科学习的过程中获得思维的生长，那么这样一个学科的教学才是有意义的. 笔者认真比较过多个学科的核心素养组成要素的表达，结果发现这些学科都在或隐或现地强调思维的重要性. 数学是一门高度注重思维的学科，当人们用通俗的语言说“数学学得好的人都聪明”的时候，实际上就是认同数学学习能够促进学生思维生长这一基本事实. 实际教学中的挑战在于，教师应当通过怎样的教学方式去促进学生的思维生长？这可不是一个容易回答的问题，无论是从经验的角度来看，还是从理论的角度来看，要想促进学生的思维生长，最关键的就是要关注学生的学习过程. 当然只有关注还是不够的，因为关注学生的学习过程，实际上只是学生学习所表达出来的信息向教师单向传输的过程，其只能够让教师对学生的学习过程有一个分析的依据，要想在此基础上促进学生的思维生长，教师还应当主动作为，在观察学生学习过程的基础上去干预学生学习，如果这一干预能够起到拨乱反正的作用，那么促进学生的思维生长也就有了坚实的基础.

学习干预不同于日常的教学，后者往往占据较强的主动性，学生是教师教学设计的被动承受者;前者虽然也具有主动性，但是这一主动性主要体现在当教师发现学生学习过程存在疏漏的时候所进行的干预. 带着这样的视角观察当下的初中数学教学实际，可以发现现实与理想的差异. 从理想的教学形态来看，课堂教学应当是师生相互分享、共同促进的过程，然而在实际的教学中，可以发现当前不少教师囿于教材，过于强调接受学习，忽视了对学生学习经验的积累和关注，包办了学生提问和质疑，影响了学生学力的发掘、自主意识的形成、思维的深度开发. 这些实际情形都是值得注意的. 心理学家皮亚杰指出：“学习知识是学生对于知识网络进行自主构建的一个过程，教师起到的只是引导和培养的作用.”所以关注生本，保证学、思并重一直是教育领域讨论的热门话题之一[1]. 而关注生本，自然就要关注学生的思维生长，同时也要关注教师对学生学习的积极干预.

本文以“中心对称”这一数学概念的教学为例，谈谈如何为学生的思维生长而进行学习干预.

“思维生长”是初中生数学学习干预的落脚点

通常情况下，做任何一件事情都需要目的，确定了正确的目的，就意味着做事有了正确的方向. 对初中生的数学学习干预也是如此，当目的确定为学生思维生长时，这就意味着思维生长应当成为初中生数学学习干预的落脚点. 对于这一观点，笔者想分三点来阐述.

第一，思维生长与学习干预是目的与过程的关系. 这一关系意味着思维生长应当是学习干预的目的，而学习干预应当在思维生长的引领下进行.

这是一个宏观认识，尽管看起来与具体的操作没有直接关系，但是如果没有这一认识或者在学习干预的时候没有这一意识，那么真正的学习干预就失去了基础. 数学学科作为一门基础性极强的学科，学生在数学学科学习过程中对方法的认识，会不知不觉地影响其他学科的学习，甚至还会影响日常生活中对事物的看待、对问题的理解等. 因此教师只有将思维生长作为数学教学的基本目的，才能将“用数学教”（而不只是“教数学”）真正落到实处.

第二，思维生长应当渗透在学生学习的每一个环节与细节当中，学习干预应当针对学生学习的环节与细节来进行.

学生的学习总是在一定的时空当中发生，在相应的时间与空间里，学生的学习往往由多个环节组成，而每个环节中又存在着诸多的细节，真正有效的学习干预应当坚持“大处着眼、小处着手”的原则，要将学习干预落实到学生的每个学习细节上，如此才能让学生的思维生长像植物汲取养分后一样获得生长.

第三，以思维生长为目的的学习干预应当基于对思维生长规律的把握.

既然对学生学习干预的目的是思维生长，那么教师就必须把握学生在数学学习过程中表现出来的思维生长规律. 对于初中生而言，思维生长规律可以概括为“在思维的过程中实现思维的生长”，因此教师的一个重要任务就是为学生创设能够激活其思维的空间，给予其足够的时间. 在足够的时间内实现空间的累积，那么思维生长也就有了极大的可能.

基于“思维生长”的数学学习干预案例及研究

对于教师而言，基于思维生长的数学学习干预研究，最好的方式就是案例研究. 此时教师要关注两点：一是干预实际的把握. 有研究表明，当学生兴趣低迷时教师进行干预，当学生产生数学疑问时教师进行干预，往往能收到较好的效果，而切实优化干预的多种方法，则是教师优化干预的基本思路. 二是干预策略的把握. 有研究认为，让学生在数学学习中“思过留痕”，可以促进学生数学思维有条理、更全面、更灵活、更深刻、系统化和可持续发展. 因此从这个角度来看，“思过留痕”可以成为学生数学思维生长的推进器，可以成为教师进行学习干预的策略权，因为它确实是一种提升学生数学思维品质的有效资源，自然也就是教师读懂学生进行因材施教的有效策略[2].

“中心对称”是初中数学“旋转”这一知识内容. 相对于其他知识而言，中心对称有一个很重要的特点，那就是其需要学生的想象力作为支撑. 有经验的教师都知道，学生在建构中心对称这一概念的时候，常常会借助想象去获得一个动态表象，这个动态表象越清晰，那么学生对中心对称图形的理解也就越准确与深刻. 想象力是思维力的重要组成部分，想象表现的建构影响着学生的思维发展. 相应地，如果教师能够基于思维发展的目的，对学生动态表象的建构过程进行积极干预，那么就可以为学生营造一个更好的学习空间. 基于这样的思考，笔者设计这一课的教学时，重点安排了以下两个环节.

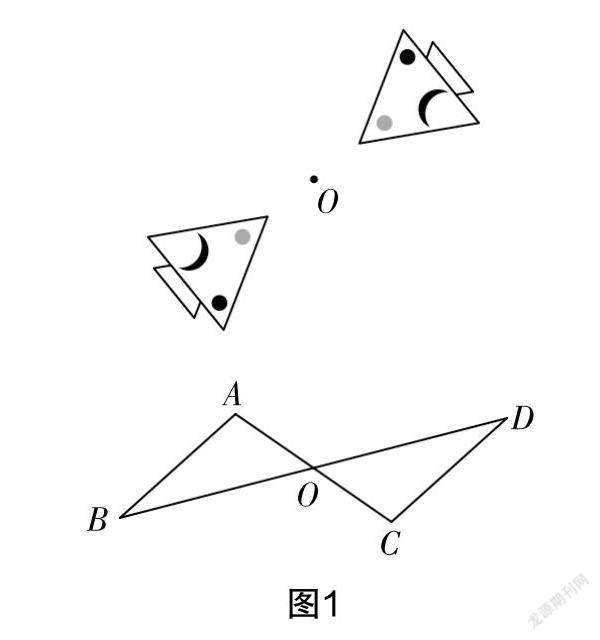
一是给学生呈现相关的图形（如图1所示），让学生去判断这些图形的共同点，让学生在证伪与比较中实现思维生长.

对于这两个图形的处理，教师千万要注意不能出现教学“越位”的情况. 所谓越位，就是剥夺学生应有的思维时间与空间，急于将答案告诉学生，不允许学生在思考的过程中出现“另类”的思维结果——这并不是说不干预，而是让学生充分暴露自己的学习事实，以提供更好的学习干预契机.

实际上对于这个教学环节，如果有足够的时间与空间，那么学生的思维过程会非常丰富. 根据笔者对于教学现场的记录，发现不少学生的第一反应就是“折叠后会重合”，甚至还有学生会直接说出“轴对称”——第一个图形还具有一点轴对称性（不关注图形中的细节），而第二个图形显然不是一个轴对称图形. 事实上，也有学生能够发现这一点，所以会对上述学生的第一反应作出否决. 这个时候部分学生出错与部分学生纠正，其实都给教师提供了良好的学习干预的契机. 教师可以针对学生的学习事实，用“你确信自己的判断准确吗？”“这真的是轴对称图形吗？”等问题来引导学生反思自己的思考结果与过程.

在这里，无论是直觉反应还是推理否決，其实都是学生思维的结果，只不过思维的水平有所不同而已. 教师容忍学生出错，并且引导学生从错误走向正确，本身就是一个思维生长的应用形态.

二是引导学生进行深度思维，促进学生思维进一步生长.

紧接着上一学习环节，当学生发现这两个图形并不是轴对称图形后，学生确实会转换思路. 如果注意观察学生的思维过程，就能发现不少学生在这个时候会想：“这些图形确实不是轴对称图形，但是在这些图形中又确实存在着一个共同的特点，那就是每个图形都是由两个相同的图形组成的，只不过这两个图形的位置关系无法通过折叠来实现重合，那么通过什么方法才能让两个图形重合呢？”有了这个问题过后，再加上本章学习的内容是“旋转”，学生自然会想到利用“旋转”来实现图形重合……这样一段文字，是笔者根据多个学生学习后的回顾总结出来的，反映了学生学习的真实情况，反映了学生的真实思维. 同时通过这样一段文字就可以发现，当学生的学习遇挫后，他们会自发地去解决遇到的问题，而这样的过程实际上就是学生的思维不断生长的过程——从最初的判断错误，到用“旋转”来解释事实，这正是思维生长的体现.

实际上学生的思维生长还不止于此，不少学生用“旋转”获得正确解释后，发现“中心对称”这个数学概念有点名不副实，原因是不少学生认为只有对折后能够重叠的才叫对称. 当学生出现这一学习困境的时候，教师就应当进行学习干预. 比如让学生对“旋转”与“对折”进行比较，通过比较，他们会发现旋转是相对于一个“点”而言的，而对折是相对于一条“线”而言的，于是就知道了“对称中心”与“对称轴”的区别，也就知道了中心对称与轴对称的本质区别. 这种认识在传统的教学当中很难发生，但是在这样的时空里，只要教师进行恰到好处的干预，学生就能形成相关的认识. 毫无疑问，这也是学生思维生长的充分体现！

学生数学学习干预中“思维生长”的评价指标

从上面的案例可以发现，在初中数学教学中，基于学生的思维生长进行学习干预，在理论上是可行的，是能够得到事实支撑的，更重要的是，这样的教学模式在核心素养发展的背景下，依然有着强大的生命力.

要知道数学学科核心素养的构建致力于学生数学抽象、逻辑推理以及数学建模等能力的发展，这些能力说到底都要得到思维的支撑. 只有思维生长了，那么这些能力才有可能发展. 因此可以说，数学思维是数学学习力的核心部分，培养数学思维是发展数学核心素养的关键[3].

当然在这个过程中还有一个重要的问题需要关注，那就是如何判断学生的思维得到了生长. 毕竟思维生长更多的只是一种感性概念，是一种经验表达，要从更加专业更加学术的角度去明确思维生长的评价指标，显然需要教师更加理性地看待学生的学习.

理性是数学学科的基本特质，同时也是数学教师应有的基本特质. 在梳理思维生长的评价指标时，笔者以为应当牢牢把握住这样几个指标：一是学生的比较能力，二是学生的推理能力，三是学生的概括能力. 比较既是一种基本的生活技能，同时也是重要的学习方法和能力，很多发现都是在比较后获得的，学生比较能力越强，往往数学学习的过程就越顺利. 推理能力就不言而喻了，数学学科核心素养当中明确提出了逻辑推理这一要素，其所强调的就是在掌握一定逻辑（对于数学来说就是数学规律）的基础上进行推理，以获得新的发现. 可以说学生推理能力的发展过程，就对应着数学规律的理解与运用过程. 概括能力是至关重要的一种能力，当学生能够用精确的语言来概括自己的学习收获，或者学习中遇到的问题时，这本身就是思维生长的重要标志.

大量的案例研究表明，只要牢牢把握住了这三个指标，那么学生的思维生长就可以得到有力的保证. 除此之外，教师不妨在平时数学教学中，正确对待学生的错误，认真分析错误原因，引导学生在错误中吸取教训，对学生的错误进行提前干预和现场跟进，能够使学生的学习顺利进行，并能逐渐提高学生观察问题、分析问题、解决问题的能力[4]. 事实也表明，学生出错的时候就是学习干预的时候，此时干预的效果往往更容易让学生形成深刻的印象.

参考文献：

[1]杜育林. 让学引思，让数学思维自然生长——以“一元一次方程章复习课”为例[J]. 中学数学教学参考，2018（17）：20-23.

[2]席爱勇. “思过留痕”：学生数学思维生长的推进器[J]. 教学月刊小学版（数学）， 2016（11）：29-31.

[3]宋雪珠，唐诗颖，王彬. 思维可视化，助力学生数学思维的生长[J]. 数学教学通讯，2021（07）：6-8.

[4]曾繁侨. 初中“数学问题”中易错点提前干预的教学探讨[J]. 福建中学数学，2017（11）：25-27.