对培养小学生思维能力的实践与思考

周楚

摘 要：数学教学其实质就是关于数学思维的教学，因此，数学教学应重视学生思维能力的培养.在日常教学中，教师要深入地研究数学、研究学生、研究教材，以学生的思维为起点，结合教学内容创设核心问题，让学生在积极的探究中有所发展、有所提升.同时，教师要重视带领学生经历观察、探索、说理、交流等活动，以此积累丰富的思维经验，提升思维品质，提高学生综合学习能力.

关键词：数学思维；思维经验；思维品质

数学教学的目的不单是让学生掌握知识、技能，更重要的是发展学生的数学思维，引导学生用数学思维解决现实生活中的各种问题，培养学生的数学思维及综合能力^［1］.那么在小学数学教学中，如何培养学生的数学思维能力呢？笔者结合教学经验谈了几点自己的看法，若有不足，请指正.

1 巧借核心问题创设思维空间

众所周知，问题在推动思维发展、提升学生学习能力等方面具有突出的价值.教师常常通过创设问题来引导学生积极思考、主动探索，以此培养学生的思维能力.表面上看，学生在思考、学习，但细细品味不难发现，教师是通过这些细碎的问题将学生的思维引导至教师预设的轨道上，这导致学生疲于应付一个个问题，却没有收获太多.要知道，在教学中设置太多的问题容易导致思维疲劳，影响学习信心和学习兴趣，因此教师要控制好问题的量与质.在教学中，为了提升问题的品质，教师应该认真地研究教材、研究学生，以学生的思维为起点创设核心问题，为学生创造思维空间^［2］.核心问题应是直指数学本质、具有一定探究空间的问题.学生需要通过多角度思考、探索、合作、交流才能更好地解决核心问题，这为思维发展提供了广阔的空间，有助于提高学生的数学综合学力.

案例1：“观察物体”核心问题设计

问题1：用4个同样大小的正方体摆一个立体图形，可以怎么摆？

问题2：你认为怎么观察可以确定这个立体图形的形状呢？

问题3：是不是只要给出三个面就能确定立体图形的形状呢？

在傳统教学中，教师大多给出具体实物，引导学生分别从正面、左面、上面观察，然后通过具体的练习加以强化，这样学生虽然知道如何观察，却不知道为什么这样观察.在本课教学中，教师突破原有的讲授式教学的束缚，借助核心问题引导学生进行全面、深入的思考，进而让学生知其然且知其所以然.问题1，通过“摆一摆”培养学生的空间观念；问题2，引导学生通过观察、思考、探究、交流等活动感悟观察几个面可以确定立体图形的形状；问题3，引导学生通过反例“辨一辨”，使其学会辩证地看待问题，培养思维的严谨性.以上三个问题具有一定的探究性和开放性，为学生的思维发展提供了广阔的空间，学生通过经历猜想、尝试、验证、调整等过程逐渐认清了问题的本质，完善和发展了学生的空间观念，提升了学生的数学应用能力.

问题在教学中的价值是毋庸置疑的，但是教师在设计问题时应以学生的发展为出发点，多设计一些有意义的、探究性的、开放性的问题，以此为思维发展提供更为广阔的空间，有效激发学生的学习潜能，提升学生的数学思维水平.

2 巧借说理引发深度思维

数学是一门非常严谨的学科，表述过程中的一字之差可能就是天壤之别，因此，在教学中要重视锤炼数学语言，让学生准确地把学习时内在的思维变化用严谨的数学语言表述出来，培养学生讲道理的好习惯^［3］.不过，小学生的语言表达能力相对较弱，在表达过程中难免会出现一些不严谨或遗漏的地方，因此教师要进行及时的启发和指导，让学生不断地调整自己的思维过程，使其语言表达逐渐走向规范化、科学化.这样通过精准的表达让学生深刻理解相关知识的同时，又使数学思维得到了激发和优化，将学生的“学”引向了更深处.

案例2：“圆的周长”教学片断

师：圆的周长与直径会存在怎样的倍数关系呢？（问题给出后，学生积极思考）

生1：我猜应该是2倍的关系.

生2：不可能，怎么可能曲线与直线一样长呢？

生3：我同意生2的说法，我们可以借助图形观察.如图1，画出任意一条直径，根据以前的知识可知，两点间的连线线段最短，显然半个圆周的长度大于直径，所以圆的周长一定比直径的2倍要长.

师：说得很好，有理有据.请大家继续猜一猜，会是几倍呢？

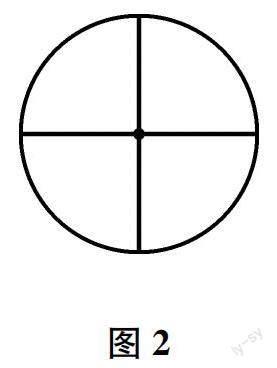
生4：如图2，我用直径把圆的周长分成4份，感觉它有4条直径那么长.

师：你们认可生4的说法吗？

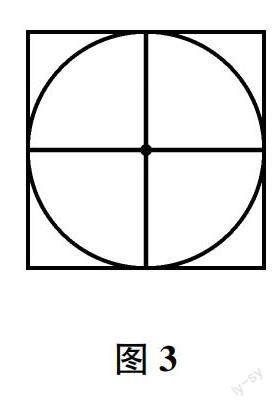
生5：我不同意这个说法.如图3，按照生4的说法可以将圆平均分成4块，观察其中一块，显然圆的一小段曲线小于正方形的两条边长之和，即小于直径，所以圆的周长应该比4条直径短.

生6：通过以上分析可知，圆的周长应该是比它直径的2倍长一些，比它直径的4倍短一些，那么它会不会是直径的3倍呢？（众生纷纷点头，表示赞同生6的猜想）

师：那么到底是不是它的3倍呢？如何验证呢？（生沉思）

生7：如图4，圆的周长比六边形的周长长，所以它应该比直径的3倍长.

师：非常好，你是如何想到利用六边形来验证的呢？

生7：我是受到前面的启发，我们在研究4倍关系时联想到了正方形，那么在研究3倍关系时可以尝试将其转化为三角形，而边长为半径的等边三角形通过旋转正好可以拼成六边形，由此得到了以上验证结果.

由此可见，数学语言不仅为师生、生生互动交流提供了便利，而且推动了学生思维能力的发展.因此，在数学教学中，教师要多鼓励学生去沟通、表达，让学生学会借助数学语言说理表达，以此让学生通过更高层次的思考、辨析活动更好地掌握数学知识，提升数学技能.

3 巧借联系促进思维发展

因受年龄特点、认知规律、思维发展水平等多种因素的影响，数学知识往往不是一下子呈现的.因此，在日常教学中，教师要适时地引导学生“ 回头看”，将散落的知识串联起来，以此让认知结构系统化、结构化，提高学生的转化和迁移能力，提高学生分析和解决问题的能力.要知道，学生的认知结构越完善，学生检索和提取信息的速度越快，越能发展学生的思维能力.因此，教师在设计教学活动时，应关注原认知，通过有效地拓展和延伸不断建立、完善学生的认知体系，以此不断丰富学生的思维活动，积累思维活动经验，发展学生的数学思维能力.

在学习过程中，教师既要引导学生“回头看”，利用旧观点看待新问题，也要带领学生“向前看”，即用新思路、新方法看待一些旧问题，让学生从已知的数学关系中推理出新的数学关系，以此培养学生的创造力，提高学生的自主学习能力，提升学生思维品质.

总之，在日常教学中，教师要认真地研究教材、研究学生，基于学生思维特点和认知规律，精心设计教学活动，将学生的思维能力培养落实到日常教学活动中，以此让学生的思维能力在学习过程中得到潜移默化地提升.

参考文献：

［1］ 李欣莲，宋乃庆，陈婷，蔡金法.小学数学教师“问题提出”表现研究［J］.数学教育学报，2019，28（2）：1-6.

［2］ 李秀娴.数学思维能力培养视角下的小学数学教学策略［J］.课程教育研究，2021（27）：185-186.

［3］ 董琪.浅谈小学低年级学生数学思维能力的培养——以“找规律”教学为例［J］.新课程导学，2021（32）：61-62.