例谈证明函数零点唯一性问题的有效策略*
2023-03-11管良梁
中学数学 2023年3期
管良梁
⦿安徽省合肥市第四中学
1 例题呈现
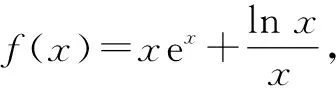
2 解题策略探究
2.1 分区间研究法
所谓分区间研究法就是将函数的定义域分成几个区间,在不同的区间里对函数进行研究.
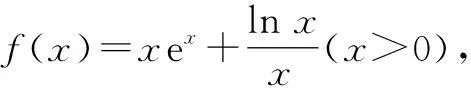
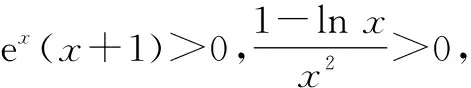
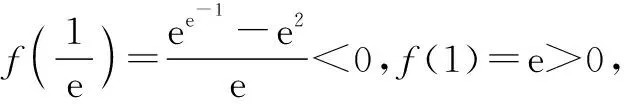
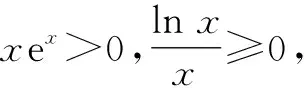
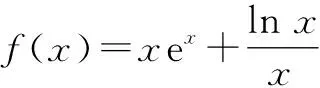

2.2 构造辅助函数法
所谓构造辅助函数法就是根据题干构造一个新的函数.借助对新构造函数的研究,解决原函数所涉及的问题.
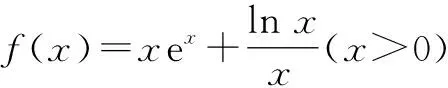

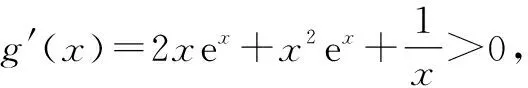
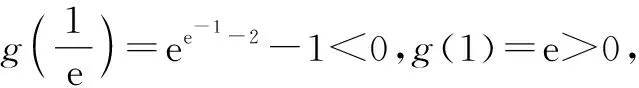
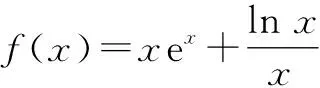
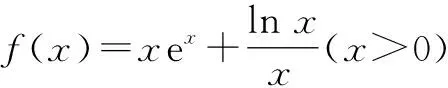
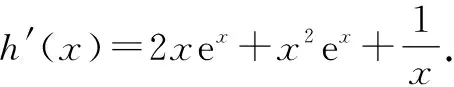

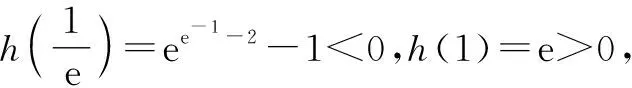
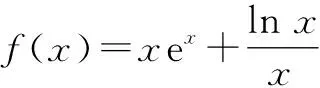
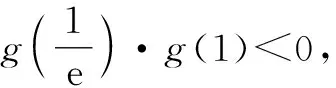
2.3 数形结合法
数形结合是一种数学思想.所谓数形结合法,就是将代数问题与几何图形结合起来,代数问题和几何问题相互转化,把复杂问题简单化.
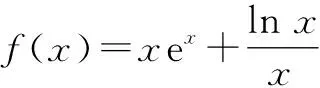
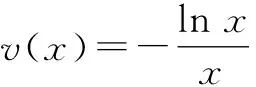
因为r(x)=xex(x>0),所以r′(x)=ex+xex=ex(x+1).
因为x∈(0,+∞),所以r′(x)=ex(x+1)>0.
故函数r(x)=xex在(0,+∞)上单调递增.
因为x→0时,r(x)→0,且x→+∞时,r(x)→+∞,所以函数r(x)=xex(x>0)的图象如图1中所示.
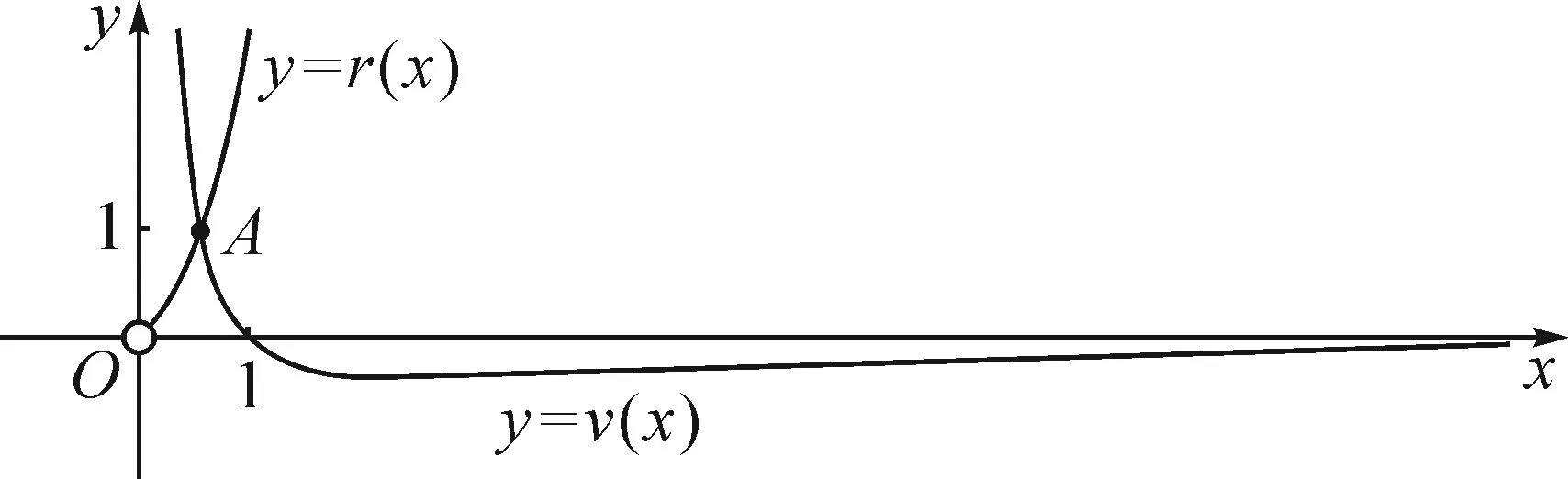
图1
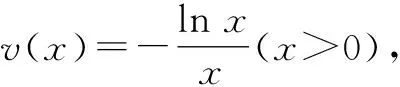
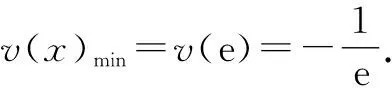
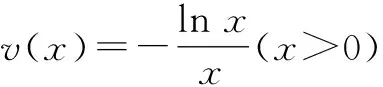
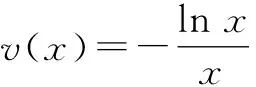
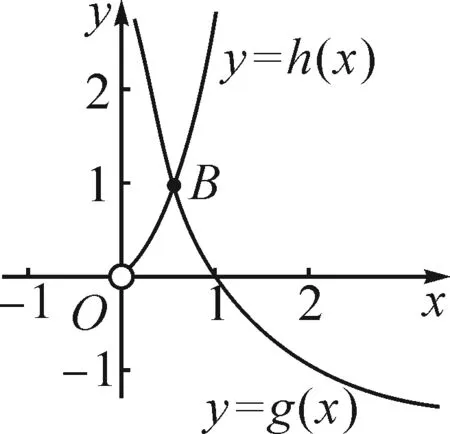
图2
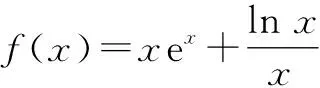
即证函数h(x)=x2ex(x>0)的图象和函数g(x)=-lnx的图象有唯一交点.
因为h(x)=x2ex(x>0),所以h′(x)=2xex+x2ex=xex(x+2).
由x∈(0,+∞),得h′(x)=xex(x+2)>0.
所以函数h(x)=x2ex在(0,+∞)上单调递增.
因为x→0时,h(x)→0,且x→+∞时,h(x)→+∞,所以函数h(x)=x2ex(x>0)的图象如图2中所示.
易知,函数g(x)=-lnx的图象,如图2所示.
由图2可知,函数h(x)=x2ex(x>0)的图象和函数g(x)=-lnx的图象有唯一交点B,所以方程x2ex=-lnx(x>0)有唯一解.
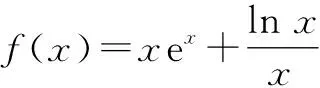
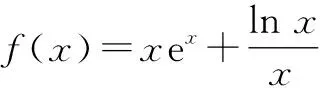
函数的零点等价于对应方程的解,也等价于对应函数图象与x轴交点的横坐标.不同的问题采取不同的方法,使得复杂问题简单化,转化为我们熟悉的函数或方程加以解答.
