利用曲线系 巧解竞赛题

梁文勇

⦿江苏省大丰高级中学

解析几何题中常涉及大量的繁琐计算，但如果选取适当方法，就可以避繁就简，使问题迎刃而解.曲线系思想是把符合某种条件的一系列曲线用带有参数的方程统一表示出来，再根据题目中的另外条件确定其中的参数或方程的特征，以此为基础，进一步解决问题[1].本文中利用曲线系对2021年的两道数学竞赛题进行解答，希望与大家交流.

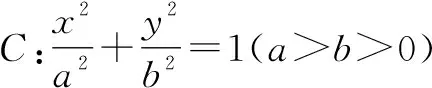
原参考答案如下：

图1

进一步得

因为a2∈(4,+∞)，所以f(a)∈(1,3).

解：由题意，设MN的方程为y=k1(x+2)，即y-k1x-2k1=0；设PQ的方程为y=k2(x-m)，即y-k2x+k2m=0.因为直线MP，NQ过M，N，P，Q四点，所以设MP，NQ两直线的统一方程为

①

②

又直线MP，NQ都过点D(1,0)，设其方程分别为x=t1y+1，x=t2y+1，则MP，NQ的方程可统一为(x-t1y-1)(x-t2y-1)=0，展开为x2-(t1+t2)xy+t1t2y2-2x+(t1+t2)y+1=0，其x2的系数与常数项相等，xy的系数与y的系数互为相反数，因此①式展开也有x2的系数与常数项相等，xy的系数与y的系数互为相反数，则有

因为a2∈(4,+∞)，所以f(a)∈(1,3).

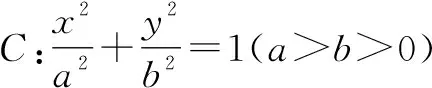
(1)求椭圆C的方程；

图2

⑤

这里也是通过A1A2，EF的统一方程的系数特征，直接找到m，n之间的关系，避免了繁琐运算.

通过两道竞赛题的解析，我们看到曲线系方法应用特征明显，结构精巧，过程简捷明快，常可减少运算，是训练数学思维、培养数学素养的好方法，在解题实践中可有意识地加以运用.

作为练习，最后留一道题：