同构在函数问题中的应用*
2023-03-11徐建新
徐建新
⦿福建省德化第一中学 福建教育学院数学教育研究所
在解决函数问题时,通过同构变形可将不等式(或等式)两边构造成具有相同结构的代数式,找出母函数并确定母函数的单调性,然后利用函数单调性求解不等式(或等式),这就是同构思想.
基本思路为:将原不等式等价变形为f(g(x)) 类型1:根据y=f(x)的单调性,将f(g(x)) 类型2:根据g(x)与h(x)的大小关系,得到y=f(x)的单调性. 本文中结合具体案例,介绍几类在函数问题中常见的同构方法. 含有地位相同的两个变量的不等式(或等式)通过变形后,不等式(或等式)两边结构具有一致性,可以构造函数. 例1(2020·新课标Ⅰ卷理数·12)若2a+log2a=4b+2log4b,则( ). A.a>2bB.a<2b C.a>b2D.a 解:由22b+log2b=22b+log2(2b)-1,得2a+log2a<22b+log2(2b).构造函数f(x)=2x+log2x,则原不等式等价于f(a) 点评:当条件中出现两个变量时,可以通过移项、两边同时除以某个式子等变形手段,将相同的自变量放在同一边,使不等式的两边具有相同的结构,从而找到母函数. 在解决同时涉及ex与lnx的相关“指对”混合等式或不等式问题时,可以灵活运用恒等式a=eln a(a>0),a=ln ea进行同构,常有如下两种方法: (1)指对“分家”:将指数形式和对数形式分开,再利用同构变形寻找母函数. (2)内部同构:以指数函数的指数位置,以及对数函数的真数位置为内函数,再利用复合函数的单调性求解. 例3(2022届泉州市第二次质量检测第8题)已知函数f(x)=ax-ex,∀x∈(1,+∞),f(x) A.(-∞,1) B.(-∞,1] C.(-∞,e) D.(-∞,e] 分析:利用x=eln x,得ex=e·eln x=eln x+1,将不等式的右边变成含有指数式的式子;也可以利用x=ln ex,得ax=aln ex,将不等式的左边变成含有对数式的式子. 解法1:因为alnx+a-ex=a(lnx+1)-eln x+1,所以f(x) 由切线不等式x-1≥lnx,得1 解法2:将不等式ax-ex aln ex-ex 故选:D. 例4(2022届T8联考第8题)设a,b都为正数,e为自然对数的底数,若aea+1+b A.ab>e B.b>ea+1 C.ab 解法1:原不等式等价于aea+1 两边同时除以e,得 aea 构造f(x)=xex,则②式转化为 f(a) 由f′(x)=(x+1)ex,得f(x)在(0,+∞)上单调递增.又aea+1 解法2:原不等式等价于 (a+1)ea+1-ea+1 构造函数f(x)=xex-ex,则④式转化为 f(a+1) 又a+1>1,lnb>1,且f′(x)=x·ex,则f(x)在(1,+∞)上单调递增,于是⑤式等价于a+1 点评:“指对”混合时,参变分离的难度比较大,而运用“指对”同构可以化难为易,但该方法对式子等价变形能力的要求较高.变形时,内部同构(相同的自变量或“自变量团”放在同一边),外部同构(母函数)自然而然显现.“指对”同构常与切线不等式综合运用,因此要熟记几个常见的切线不等式及其变形式. 以下是四个常用的切线不等式(如图1,图2): (1)ex≥x+1(当且仅当x=0时等号成立); (2)lnx≤x-1(当且仅当x=1时等号成立); (3)ex≥ex(当且仅当x=1时等号成立); 图1 图2 由切线不等式ex≥x+1(当且仅当x=0时等号成立),得xex=eln x+x≥x+lnx+1(当且仅当lnx+x=0时等号成立),即xex≥x+lnx+1. 例5若函数f(x)=x(e2x-a)-lnx-1无零点,则整数a的最大值是( ). A.3 B.2 C.1 D.0 解:由切线不等式,得f(x)=eln x+2x-ax-lnx-1≥(lnx+2x+1)-ax-lnx-1=(2-a)x. 因此,f(x)无零点时整数a的最大值是1.故选:C. 例6(2020年新高考Ⅰ卷第21题节选)已知函数f(x)=aex-1-lnx+lna.若f(x)≥1,求a的取值范围. 解法1:不等式aex-1-lnx+lna≥1,等价于eln a+x-1-lnx+lna-1≥0. 移项,得eln a+x-1+lna-1≥lnx. 两边同时加x,得 eln a+x-1+lna+x-1≥x+lnx=eln x+lnx.⑥ 构造g(t)=et+t,则g(t)在R上是增函数,且⑥式转化为g(lna+x-1)≥g(lnx).所以lna+x-1≥lnx,即lna≥lnx-x+1在(0,+∞)上恒成立. 设h(x)=lnx-x+1,则由lnx≤x-1,得h(x)的最大值为0,从而lna≥0,解得a≥1. 故a的取值范围为[1,+∞). 解法2:不等式aex-1-lnx+lna≥1,等价于eln a+x-1-lnx+lna-1≥0. 又eln a+x-1≥lna+x,所以要使f(x)≥1恒成立,则2lna≥(lnx-x+1)max. 设g(x)=lnx-x+1,则可知g(x)max=g(1)=0.所以2lna≥0,解得a≥1. 故a的取值范围为[1,+∞). 点评:解法1在不等式eln a+x-1+lna-1≥lnx的两边同时加“x”,使左边出现与指数幂相同的“自变量团”,右边变形成eln a+x-1+lna+x-1≥eln x+lnx,运用的是“指对”同构.解法2在不等式eln a+x-1-lnx+lna-1≥0中运用朗博同构,更直接迅速. 指数幂和对数的真数相差1时,可用“差一同构”.下面仍以例6为例,利用“差一同构”进行分析. 构造函数g(x)=ex-x-1.由切线不等式,可知ex≥x+1(当且仅当x=0时,等号成立).所以,g(x-1)=ex-1-x≥0,g(lnx)=x-lnx-1≥0(当且仅当x=1时,等号成立),两式相加,得ex-1-lnx-1≥0(当且仅当x=1时,等号成立). 当a≥1时,lna≥0.所以aex-1-lnx+lna≥ex-1-lnx≥1恒成立. 当0 综上,可知f(x)≥1时,a≥1. 以上由母函数g(x)=ex-x-1同构出函数g(x-1)和g(lnx),结合切线不等式得到两个取等号条件一样的不等式,从而轻松破解该题.同样地,由g(x)=ex-x-1≥0,也可以构造g[ln(x+1)]=x-ln(x+1)≥0,两式相加,得ex-ln(x+1)-1≥0(以上三个不等式都是当且仅当x=0时,等号成立).因此,取等号条件是差一同构的关键. 总之,通过上述多种同构方法的归类剖析可知,处理此类问题切入点虽有不同,但目标一致,关键在于灵活运用恒等式xex=ex+ln x等,对题设的等式或不等式进行适当的变形,使之左右两边结构相同,进而寻找母函数.该类问题又常与切线不等式综合运用,解法多样,变形难度较大.因此,要学会利用同构变形,在掌握思想与方法的过程中不断形成知识体系,提升数学品质,提高思维能力.1 双变量同构
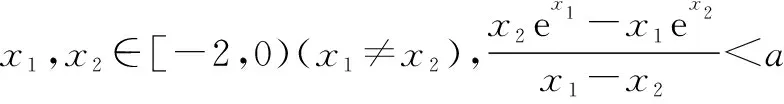
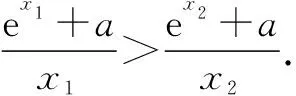
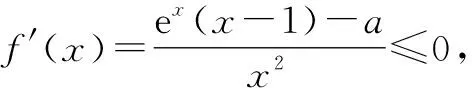
2 “指对”同构

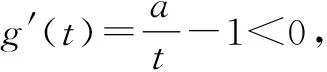
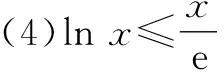
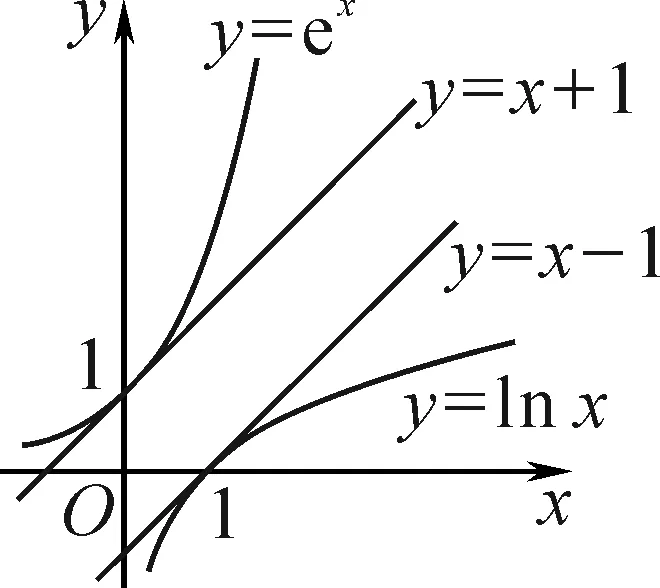
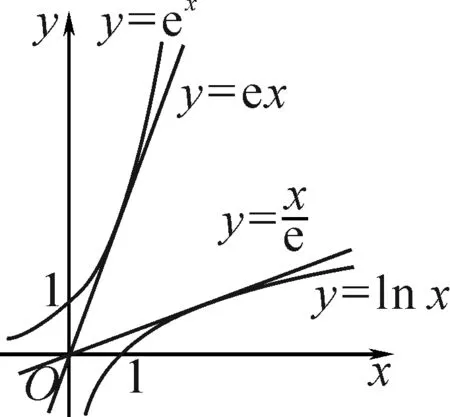
3 朗博同构
4 差一同构
