源于新教材习题的说题案例及教学启示

肖松柏 张 璐

⦿新疆乌鲁木齐市第四十一中学

2022年4月，市教研中心举办了高中数学教师说题比赛，要求所选试题必须是人教A版高中数学(2019版)必修第一册或必修第二册中的例题或习题.目的就是鼓励教师学习新教材、钻研新教材，以教材为本，以课程标准为纲开展教学，纠正以前那种脱离教材搞教学，忽视教材中典型例题和习题的不妥做法.本文中以本次说题比赛所选习题为例，谈谈对新教材习题的认识.

1 说题案例

图1

1.1 说题目来源

本题选自人教A版高中数学(2019版)必修第二册第23页习题6.2综合运用第15题，主要考查平面向量的线性运算.

1.2 说题目考查的核心素养

本题属于向量问题中的高频考点，在解题中应用平面向量基本定理、向量加减法法则、向量运算才能得到解决.考查的核心素养有逻辑推理、数学运算、直观想象.

1.3 说解题方法

评析：本证法主要用到向量的加法法则及“算两次”的方法.

证法2：如图2，延长EF至点G，使EF=FG.

因为F是BC的中点，所以BF=CF.

图2

因此四边形EBGF是平行四边形.

评析：证法2主要通过构造平行四边形，应用向量加法的平行四边形法则.

图3

证法3：如图3，延长BA,CD交于点O，连接EO,FO.

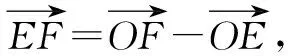
评析：证法3主要应用了由证法2得出的中线向量结论，简化计算.

图4

证法4：如图4，过点B作BG∥DC，使BG=DC，则四边形BGCD是平行四边形.

因为F为DG的中点，E为AD的中点，所以EF是△AGD的中位线.

1.4 说结论应用

本题结果可以作为一个结论，灵活应用该结论在解题中可以简化计算.

图5

解：如图5，取AD,AB,BC,CD的中点分别为E,G,F,H.

所以AC=3.

1.5 说变式拓展

如果变换习题中的四边形，结论仍然成立，会为解决问题带来很多方便.

这个结论称为中线长定理.即为人教A版高中数学(2019年版)必修二第53页习题6.4第15题:

△ABC的三边分别为a,b,c，BC,CA,AB边上的中线分别记为ma,mb,mc，利用余弦定理证明：

图6

1.6 说教学价值

从本习题的证明可以得到中线向量结论，继而证明中线长定理.向量的分解一直是学生的难点，从几道变式题可以看出，学生只要立足教材，真正理解并体会有关解法，对其相关的变式问题也很容易解决.因此对教材中的典型例题、习题进行研究，开展“一题多解、一题多变、多题同解” 的训练，可以提升学生的能力.本题涉及向量的分解，加减法的计算，平行四边形法则的应用，是高考的命题热点，作为例题极具典型性、作为习题极具训练价值.

2 教学启示

2.1 提高对教材习题重要性的认识

本次说题比赛，市教研中心之所以要求必须选择新教材中的例题或习题，目的就是要引导教师钻研新教材、研读新教材，关注重点例题和习题，纠正抛开课本围绕一本复习资料或自编讲义教学的错误做法.对于教材在教学中的作用，《普通高中数学课程标准(2017版2020年修订)》指出：习题是教材的重要组成部分，要提高习题的有效性，科学、准确把握习题的容量、难度.习题是课堂教学内容的巩固和深化，也应当为学生发展数学学科核心素养提供平台[1].但在潜意识中学生和教师都觉得课本习题过于简单而常被忽视，违背了教材设置习题的初衷.但在2019年版新教材中习题设置进行分层，可以满足不同程度学生的需要，加之“源于课本、高于课本”是高考命题的一条原则，因而教学中要提高对教材习题重要性的认识.

2.2 熟悉习题设置，布置作业有的放矢

教材中的习题是编写者为巩固教材知识内容，实现课程标准要求精心设计的，具有基础性、典型性和发展性，因此教师必须熟悉习题设置，布置作业有的放矢.教材中每小节内容后都设置了“练习”，这类习题紧扣本节新知，难度不大，目的是帮助学生理解和掌握本节课知识点，一般在课堂上完成.每一大节后都设置了“习题”，综合了这一大节的所有知识点，具有基础性、综合性、探究性的特点.“复习巩固”习题，主要复习本大节的主要知识点，适合基础较弱的学生完成.“综合运用”习题具有一定的难度和综合性，适合中等基础的学生完成.“拓广探索”习题综合性更强，还具有发展性，需要引导学生完成.新教材中习题的分层设置，有利于满足不同基础学生的需求，有利于激发学生学习积极性.

2.3 对重点习题适当拓展研究

教材中设置的习题除了具有巩固新知的功能，还承载着拓展延伸新知的功能[2].教师可以选择具有典型性、灵活性、层次性、巩固性的习题，引导学生进行研究型学习.比如说题比赛选择的这道习题，考虑它有哪些解法，能不能变式，是否隐含有结论，结论如何应用，等等.又如必修二第53页“习题6.4”第10题：你能用三角形的边和角的正弦表示三角形的面积吗？这其实就是正弦定理的面积公式，现在以习题形式出现，就是要求学生在证明的基础上会灵活应用.再如“习题6.4”第21题是一道研究方案的试题，可以参考必修二第49页例2.所以学生和教师都要转变对教材习题简单而被忽视的做法.

2.4 针对习题完成情况及时讲评和评价

习题还具有评价功能.教材中的习题多作为每天的课后作业，学生通过完成习题巩固消化本节内容，及时发现存在的问题，教师及时批改作业，及时发现作业中暴露出来的问题，并及时讲评，及时评价，可提升基础较弱学生的获得感、自信心，可以激发学生学习数学的热情.同时通过学生完成习题情况反馈进行教学评价，及时调整教学策略，达到教学相长的目的.