应变对二维WSe2材料磁性影响的计算研究

＊韩医临 宁福林 杨梦雪 任杰 王敏

（1.河北政法职业学院建筑工程与法务系 河北 050046 2.河北科技大学信息科学与工程学院 河北 050018 3.河北科技大学理学院 河北 050018）

1.引言

石墨烯的出现使二维材料的研究被人们广泛关注[1]，其中具有半导体性质的过渡金属硫族化合物（简称TMDs）尤为突出。一方面，TMDs具有高载流子迁移率、较小的电阻率和电容等优异的电学性质[2]，有潜力应用于电子学和导电材料等领域[3]。另一方面，TMDs具有优异的光学性能，能够吸收宽波长的光谱范围，并表现出明显的荧光和光致发光等现象[3]。有应用于光电转换器件、光电探测器等领域的潜力。

TMDs的化学式可用MX2表示，其中M是过渡金属（IV族或VI族），如铜、钛、钒等，X是硫族元素（S、Se或Te）[4]。每一层都由一个中心金属原子（M）与两个硫原子（X）形成八面体配位，其中一层过渡金属原子（M）夹在两层硫族原子（X）之间，单层内硫族原子和金属之间存在强共价键，两层之间通过弱范德瓦尔斯力相互作用结合在一起[5]。在二维TMDs中，这些层之间的相互作用会导致不同的堆叠方式和晶体结构。

绝大部分TMDs材料例如MoSe2是n型半导体材料，而二硒化钨（WSe2）作为TMDs中带隙相对较大的重要成员，在自然环境下为黑灰色，是首个被验证同时具有n、p型导电特性的半导体，表现出优异的电学性能。典型的研究，如Wang L等[6]计算研究了过渡金属掺杂WSe2/磷酸化烯结构上的吸附行为，结果显示TM杂质的结合降低了吸附距离，增加了吸附能及电荷转移。Guan Y等[7]研究了Al、Ga、C、N、O、F、F、P、S和Cl原子掺杂，以及双氧原子掺杂对BAs/WSe2异质结构、电子和磁性的影响，结果表明掺杂了Al、Ga、N和P原子的体系与B或As原子结合，基本上保持了原始体系的直接带隙宽度。Nupur Navlakha等[8]研究了二维材料异质结构的能带对准，将黑磷与电负性较低的材料WSe2、MoSe2和WS2结合的计算结果显示跨跃（Type I）对准，其中WSe2和MoSe2呈现直接能隙，而WS2呈现间接能隙。

先前的研究对WSe2单层体系中本征缺陷及应力应变的情况较少涉及。在本文的研究中，采用了基于密度泛函理论的第一性原理计算方法，计算研究单层WSe2的电子结构性质，尤其是W空位可以直接改变材料的磁性，施加应变也可以使Se空位系统产生自旋极化。

2.研究方法与模型

本文采用维也纳从头算模拟软件包（VASP）进行电子结构方面的计算[9]，采用广义梯度近似GGA[10]、投影缀加波PAW方法处理材料中电子之间[11]、原子实与价电子之间的相互作用。计算过程中，建模得到48个原子的单层WSe2材料，其中灰色球体表示W原子，黑色球体表示Se原子。为了消除层与层之间的镜像相互作用，本文添加了10Å的真空层。完美的单层WSe2的（001）面的模型见图1所示。晶格常数为：a=13.3Å，b=13.3Å，c=15.3Å，α=90°，β=90°，γ=120°。在电子结构计算中对WSe2采用4×4×1的k网格，其空间群为P63/MMC。

图1 单层WSe2材料模型

3.结果与讨论

(1)完美WSe2(001)单层表面

在图2中，0eV处为费米能级EF所在位置，费米能级左侧表示全占据态的态密度，也称为价带态密度。占据态是指在绝对零度时材料中所有电子都填充到最低能量的态。在总态密度图上，价带态密度反映了材料中价带上电子的分布情况，即处于价带能量范围内的电子数目。费米能级右侧表示未占据态的态密度，也称为导带态密度。未占据态是指在绝对零度时材料中尚未被填充的能级，其能量高于费米能级。在总态密度图上，导带态密度反映了材料中导带上电子的分布状况，即处于导带能量范围内的电子数目。禁带位于导带底和价带顶之间，由于费米能级在导带和价带之间，可以看到在完美体系无缺陷情况下，WSe2是一个半导体，其禁带宽度约为2.1eV。自旋是电子的内禀性质之一，可以分为向上自旋和向下自旋。在材料中，电子的自旋会影响材料的磁学性质和输运性质等。在总态密度图中，上半部分表示自旋向上，下半部分表示自旋向下。自旋极化态密度是指自旋向上态密度和自旋向下态密度的差异，它表示了材料中电子自旋对态密度的贡献。如果自旋向上态密度和自旋向下态密度对称或相等，则自旋极化态密度为零，材料是非磁性的。而如果自旋向上态密度和自旋向下态密度不相等，则自旋极化态密度不为零，材料是磁性的。因此从图2可知，完美WSe2材料是非磁性的。

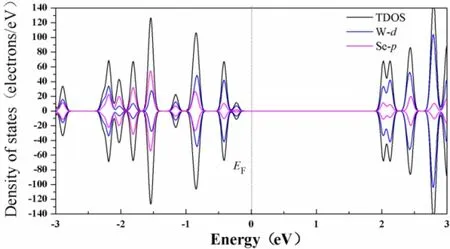
图2 单层完美WSe2材料态密度图

下面对施加了0%、2%、4%、6%、8%、10%应变的完美WSe2材料进行静态计算，研究发现随着拉伸应变的增大，WSe2体系的能量变大，禁带宽度逐渐变小，这和文献[12]类似。这是因为拉伸会导致电子在晶格中的有效质量发生变化，使它们更容易穿越禁带，从而降低了禁带宽度。见表1所示。

表1 施加0%～10%的应变下完美体系WSe2的禁带宽度情况

随着应变的增加，很显然禁带宽度有减小的趋势，这主要是由于应变导致晶体结构产生了较大的畸变，畸变使得晶体场发生变化，导致导带底与价带顶的能级扰动，使得带隙变小。

(2)本征空位对WSe2(001)单层表面磁电子性质的影响

在完美体系WSe2模型的基础上，只需要在合适位置上删去一个Se或W原子，就构建成带有本征空位缺陷的WSe2结构模型。研究发现对于Se空位的情况，随着拉伸应变的增大，体系的能量变大，禁带宽度逐渐变小。并且，在施加0%～6%的应变时，自旋向上态密度和自旋向下态密度相等，材料是非磁性的。而在8%、10%的应变下，自旋向上态密度和自旋向下态密度不相等，材料具有了磁性，这是因为，当材料受到应变时，其晶格结构会发生变化，从而影响材料的电子结构和磁矩分布，最终导致材料的磁学性质发生了变化。具体来说，施加拉伸应变可以改变材料的晶格常数和化学键长度，从而影响材料中电子的排布和相互作用。这些变化可能会导致材料中原本不存在的磁性区域出现，或是原本存在的磁性区域的磁矩大小和方向发生变化。此外，应变还可能影响材料的自旋轨道耦合和电子局域化等，进而也会影响材料的磁性。缺失一个Se原子的WSe2在应变较小时没有磁矩，而当应变达到一定值时磁矩会突增。这是因为当施加的拉伸应变较小时，WSe2的晶格结构会发生略微的变化，不会影响到磁性。然而，随着应变的增加，晶格结构会发生更大程度的改变，导致W原子的位置发生偏移，从而使W原子的d轨道发生变化，进而影响到了磁矩的大小。当应变达到一定程度时，WSe2的晶格结构发生了足够的变化，使得W原子的d轨道发生了明显的改变，从而导致磁矩的突然增大。详见图3a所示。

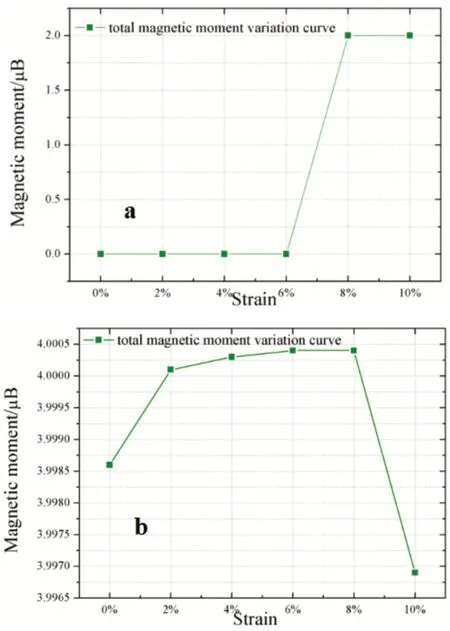
图3 含本征缺陷的WSe2单层材料磁矩随应变的变化

同样对于W空位的情况，研究显示二维表面体系将会变成一个具有金属能带特征的材料，且体系会产生磁性。对于缺失一个W原子的WSe2材料，当施加拉伸应变时，晶格常数会发生变化，从而影响电子的运动和排布。在一定程度上，这种应变会导致局部电子的自旋极化，从而导致磁矩的变化。当施加小的拉伸应变时，由于晶格略微扩张，W和Se原子之间的距离变大，从而使得W原子的d轨道发生略微的裂分，导致局部自旋极化程度增加，磁矩也相应略微增大（相对值变化不大）。但是，当拉伸应变进一步增大时，晶格常数继续增加，W和Se原子之间的距离变得更大，此时W原子的d轨道发生了更大的裂分，但是这种裂分会导致d轨道的一些电子填满了原本空的能级，从而抵消了自旋极化的效应，导致磁矩略微减小甚至消失。因此，对于缺失一个W原子的WSe2材料，当施加拉伸应变时，磁矩的改变整体很微弱。详见图3b所示。

4.结论

通过计算完美体系WSe2单层结构模型的态密度图，可以发现完美体系WSe2的禁带宽度约为2eV。并且由于态密度图中自旋向上和自旋向下的态密度相等，所以完美体系WSe2是一个没有磁性的绝缘体，且在0%～10%的应变下不会产生磁性。缺失一个Se原子的WSe2在应变较小时没有磁矩，而当应变达到一定值时磁矩会突增；当WSe2被挖去一个W原子后，其电子结构会发生显著改变，会有磁矩产生，进一步研究表明拉伸应变对磁矩的影响很微弱。