冲击载荷作用下Q345钢失效应变与单元尺寸关系研究

2023-03-01伍星星刘建湖陈嘉伟王海坤张伦平

船舶力学 2023年2期

伍星星，刘建湖，陈嘉伟，王海坤，张伦平

（中国船舶科学研究中心，江苏无锡 214082）

0 引言

得益于计算机硬件水平和有限元分析技术的快速发展，数值仿真手段已成为研究结构在强冲击载荷作用下动态毁伤破坏响应的一种重要手段，准确预测结构的毁伤模式关键在于确定材料的失效应变。随着研究的深入，发现单元的失效应变对网格尺寸具有很强的依赖性。孟利平[1]等以材料拉伸试件为研究对象，指出单元失效应变与网格尺寸间呈反比关系，并拟合给出了二者的关系表达式；尤小健等[2]以平板和加筋板为研究对象，采用常应变失效准则，发现随着网格尺寸的增大，不管是加筋板还是平板，都呈减小的趋势，但变化曲线明显不同；Korgesaar 等[3]以落锤冲击作用下平板、加筋板试验结果为依据，研究了不同网格尺寸（L/t=2,5,8,20，L为网格尺寸，t为板厚）对锤头冲击力时程曲线、结构破坏区域的影响；同时Korgesaar 等[4]通过对单轴拉伸试件、双轴拉伸试件破坏进行模拟，更进一步指出单元失效应变与网格尺寸之间的关系还与结构所处应力状态有关，如单轴拉伸试件的失效应变比双轴拉伸试件对网格尺寸更加敏感；Alsos 等[5]通过对S235JR 钢开展单轴拉伸试验，基于Barba 准则，给出了失效应变与网格尺寸之间的关系式：

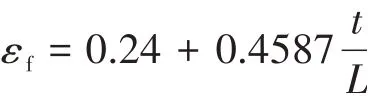
式中，t为板厚，L为网格尺寸。

单元失效应变对网格尺寸具有很强的依赖性，但现阶段国内外尚未有学者能定量给出可用于工程计算的二者之间的表达式，对于深层次的影响机理问题也鲜有人进行深入挖掘，众多学者为排除网格尺寸的影响，常采用将结构单元尺寸细化至对计算结果无影响的做法[6-10]。诚然，对于较小结构（如材料力学性能试件），可采用该做法，但对于工程中常见的大质量弹体穿甲问题、船舶碰撞问题、舱段模型爆炸冲击响应问题等，采用较小的网格，仿真计算难以继续开展下去，计算效率也会大大降低，因此迫切需要深入研究网格尺寸与失效应变之间的关系。本文以开展的压缩试件、扭转试件、圆棒拉伸试件、缺口拉伸试件、平板拉伸试件断裂试验为基础，借助数值仿真手段建立单元失效应变与网格尺寸之间关系，从机理层面揭示网格尺寸对单元失效应变的影响规律，从而为后续穿甲、舰船抗爆等工程问题仿真计算所涉及的失效应变取值提供依据。

1 Q345B钢断裂力学性能试验

对Q345B 钢开展断裂力学性能试验[11]，试件类型主要包括光滑圆棒拉伸试件、缺口圆棒拉伸试件、平板拉伸试件、扭转试件、压缩试件等，均取自同一批钢板，各类试件尺寸见图1，参照GB/T 228-2002 制作，缺口拉伸试件半径R有2 mm、6 mm、8 mm 和18 mm 等四种。光滑圆棒及缺口圆棒拉伸试件试验在WDW-100DIII 微机控制电子万能试验机上开展，在试件标距段安装引伸计，引伸计标距为50 mm，量程为25 mm。扭转试件试验在NDW-500Ⅲ微机控制电子万能试验机上进行，采用专用扭转试验夹具，试验机的两夹头之一可以沿轴向自由移动，对试件无附加轴向力，两夹头保持同轴。压缩试件试验在WDW-100DⅢ微机控制电子万能试验机上进行，试件与试验机的接触面预制了倒角，以避免试验时试件接触面边缘产生应力集中。平板试件拉伸试验在中国船舶科学研究中心振动噪声实验室MTS 材料试验机上进行，试件厚度为3.76 mm。每类试件均进行5 次重复试验，以保证试验数据的有效性。

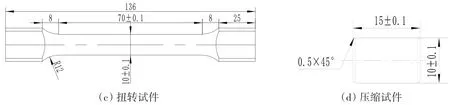
图1 各类试件尺寸示意图Fig.1 Dimensions of different specimens

图2 拉伸试件力-位移曲线示意图Fig.2 Curve of force-deformation of tension specimens

圆棒及缺口圆棒拉伸试件试验后的力-位移曲线如图2所示，表1给出了各拉伸试件的试验测量结果，试件断后延伸率通过测量试件断裂前后伸长量得出，试件端面收缩率通过测量试件颈缩部位直径变化得出，试件失效应变通过如下公式求出：

式中，S0为试件的初始横截面直径，S为断口直径。

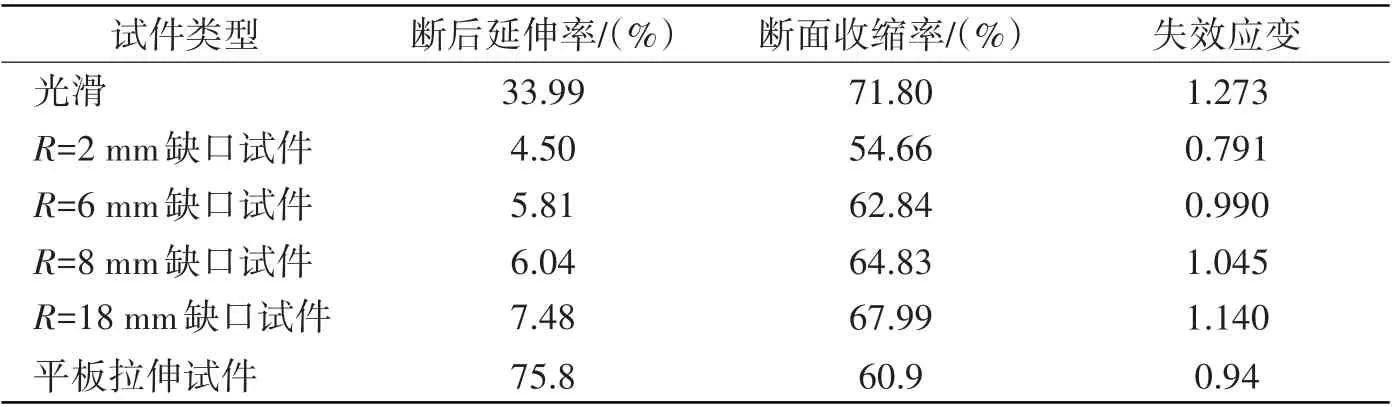
表1 拉伸试件试验测量结果Tab.1 Results of tension specimens

对于扭转试件，其扭力-转角曲线如图3（a）所示。扭转过程中试件变形较为均匀，Q345B 钢断裂时产生的转角为35 rad，断裂应变为1.340，按如下公式计算[12]：

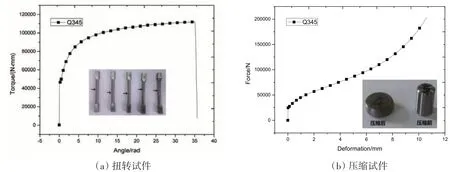
图3 扭转、压缩试件力-位移曲线示意图Fig.3 Curve of force-deformation of torsion and compress specimens

式中，H为试件表面的切应变（扭转角度），

其中，θ为试验机旋转角度，R为试验段直径，l为试验段标距。

对于压缩试件，其压力-位移曲线如图3（b）所示，试验中试件未出现典型的45°方向裂纹，未发生破坏，但在压缩过程中由于试件两端与试验机压头之间的摩擦作用力，试件被压缩成圆鼓状，最终Q345B钢压缩率为63%。

2 网格尺寸对失效应变影响机理分析

2.1 计算模型

本节主要利用有限元软件Abaqus进行分析，光滑圆棒、缺口试件、扭转试件、压缩试件均采用二维轴对称模型，平板拉伸试件采用实体单元建立，建立1/2对称模型，模型一端固定，另一端施加位移或者转角载荷。由于本节的目的在于比较不同网格尺寸下单元的失效应变，因此计算模型中不设置失效判据，当试件达到试验获得的最大位移或者转角时，此刻试件的最大等效塑性应变视为断裂应变。

图4 各类试件有限元模型示意图Fig.4 Numerical simulation models of specimens

图5 试件试验和有限元计算载荷位移曲线对比示意图Fig.5 Comparison between experiment results and simulation results

各类试件的仿真计算模型见图4，仿真计算过程中材料本构模型输入圆棒拉伸试件获取真实应力应变值，计算过程中需反复调试输入应力应变值（颈缩后阶段应力应变值），直至保证计算输出的载荷位移曲线与试验曲线一致，具体方法见文献[13]，图5显示的是试件试验载荷位移曲线与有限元计算结果对比。针对光滑圆棒试件、缺口试件、扭转试件、压缩试件等二维轴对称模型，通过计算发现当计算模型网格尺寸小于0.1 mm时，网格尺寸对试件断裂应变的影响可基本忽略；针对平板试件的实体计算模型，发现当中间试验区域网格尺寸小于0.2 mm时，网格尺寸对试件断裂应变的影响基本可忽略。后文将在此基础上依次计算不同网格尺寸下（0.1 mm、0.25 mm、0.5 mm、1 mm、1.5 mm、2 mm、2.5 mm）各类试件在断裂时刻的失效应变，用于揭示网格尺寸对单元失效应变的影响规律。

2.2 结果分析

表2 给出了不同网格尺寸下各类试件的失效应变值，当试件达到试验获取的最大位移或者转角时，取此时试件破坏点位置等效塑性应变为失效应变。对于扭转试件，试件外表面为起始破坏位置，且最大塑性应变亦分布在外表面；对于圆棒拉伸试件，试件中心位置为起始破坏位置，该位置应力三轴度、等效塑性应变在断面位置均最大；平面拉伸试件与圆棒拉伸试件起始破坏位置基本一致。从计算结果来看，对于扭转试件、光滑圆棒拉伸试件、平板拉伸试件，采用细网格计算获得的失效应变较试验值偏大。主要原因是断口截面各位置等效塑性应变分布不一致，而试验值通过测量断面收缩率来反推失效应变，本质结果为断口平均应变，但仿真结果取得的基本为断面塑性应变，因此较试验测量值偏大。但对于缺口试件，细网格仿真计算值却小于试验值，内在原因还需后续进一步研究。

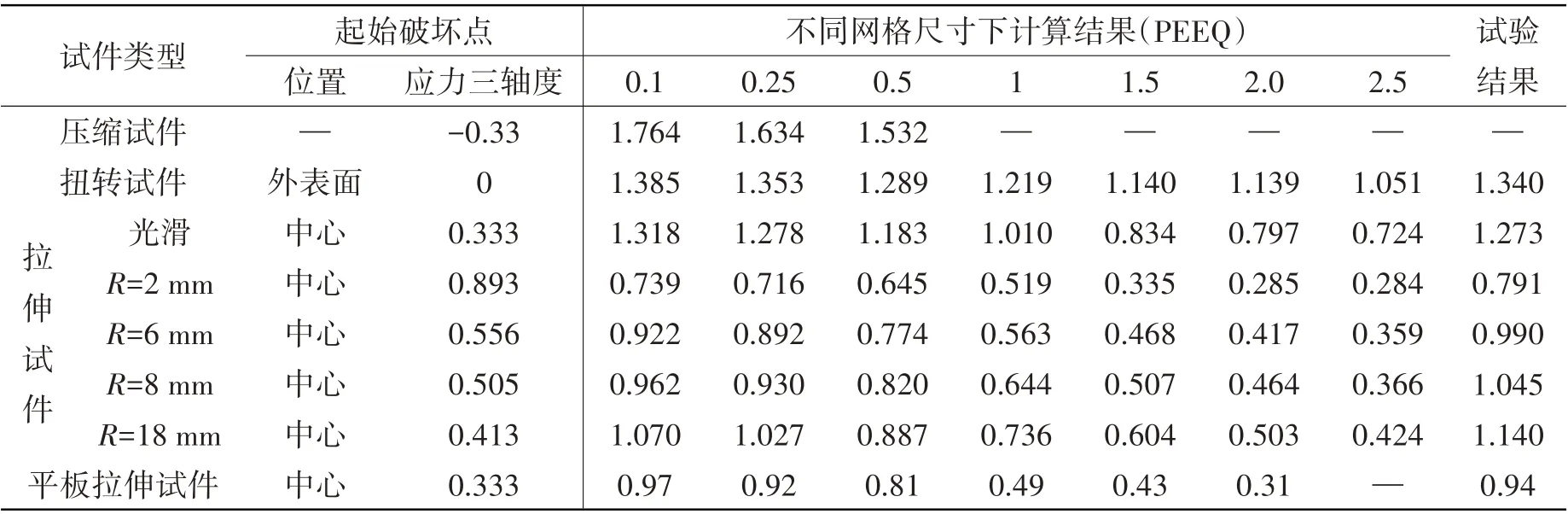
表2 材料失效应变与网格尺寸之间关系对比Tab.2 Variation of failure strain with element mesh size

总体来看，网格尺寸对单元失效应变计算结果具有较大的影响，网格尺寸越大，单元失效应变值越小。主要原因是试件在受载过程中，塑性大变形区域往往集中在试件局部区域，如拉伸试件的颈缩区域、扭转试件外表面区域等，当网格尺寸较小时，局部区域的塑性变形可充分模拟，此时单元的失效应变与试件的真实断裂应变较接近，而当网格尺寸较大时，此时局部塑性区域被包含在大尺寸单元的局部范围，原本真实的塑性应变被平均到大网格单元，因此大网格单元的失效应变减小。图6是不同网格尺寸下试件等效塑性应变分布示意图，以断裂时刻红色区域即试件最大等效塑性应变分布为例，当网格尺寸越小时，红色区域范围内包含的网格数量就越多，此时单元等效塑性应变最大。

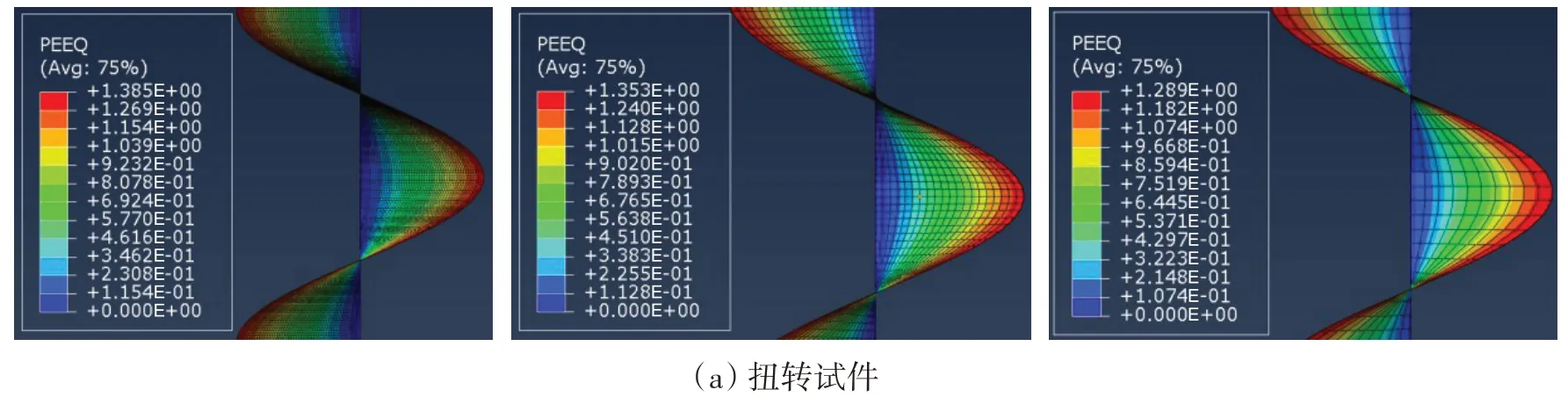
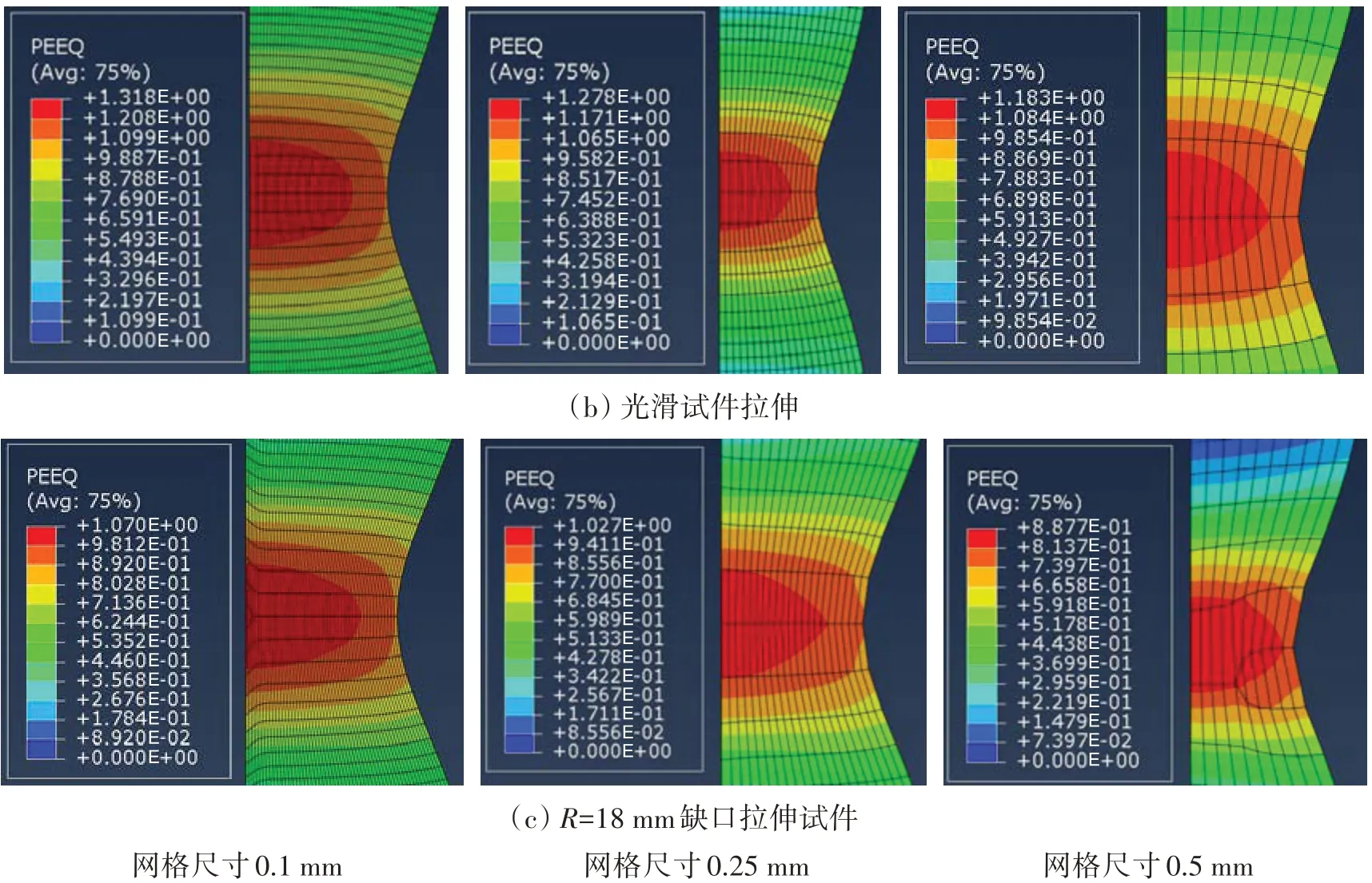
图6 不同网格尺寸下试件断裂时刻等效塑性应变分布示意图Fig.6 PEEQ distribution of typical specimen under different element sizes

此外，试件类型对失效应变随网格尺寸的衰减趋势具有一定的影响。以光滑圆棒试件、缺口圆棒试件（R=2 mm、R=6 mm、R=8 mm、R=18 mm）、圆棒扭转试件为例，图7依次给出了网格尺寸2.5 mm、1.0 mm 所对应的单元失效应变相对0.1 mm 时的减小百分比，其中横坐标表示的是试件所处的初始应力三轴度，纵坐标表示的是单元失效应变衰减百分比。综合可看出，缺口圆棒试件（R=2 mm、R=6 mm、R=8 mm、R=18 mm）对网格尺寸最敏感，失效应变衰减最快，其次依次是光滑拉伸试件、扭转试件，即试件所处应力三轴度越大，随网格尺寸衰减越快。

综上来看，网格尺寸对单元失效应变影响主要归咎于如下因素：

（1）试件撕裂破坏前，塑性变形往往集中于局部区域，如拉伸试件的颈缩区域、扭转试件外表面等，小单元可充分模拟局部区域的塑性变形分布，大单元却将局部区域的塑性变形进行平摊，致使单元对应的失效应变减小。若局部区域在大单元中所占比例较小，如实尺度船体模型中，单元尺寸往往在100 mm 以上，撕裂破坏前的局部塑性区域相对单元尺寸占比较小，此时失效应变可直接取材料颈缩之前的均匀应变；

（2）网格尺寸对单元失效应变的影响还与单元所处应力三轴度存在一定的关系，当所处应力三轴度越大时，失效应变衰减越快。不同的冲击物理过程（侵彻、爆炸）需要依据各自的受力状态建立所对应的失效应变与网格尺寸之间的关系。

图7 单元失效应变衰减百分比与试件类型关系示意图Fig.7 Schematic diagram of relationship between element failure strain attenuation percentage and specimen type

3 冲击载荷下单元失效应变取值方法

3.1 弹体穿甲仿真计算

针对弹体侵彻仿真计算，弹体侵彻过程中变形破坏区域基本集中在弹靶接触区域，依据前文的分析结果，单元失效应变取值与弹靶接触区域网格密集度、弹靶接触过程中受力状态有关。基于此，弹体穿甲仿真中失效应变取值应参照如下原则：

（1）弹靶接触区域网格密集度主要以弹径范围内单元网格数量来体现，重点建立失效应变取值与单元网格尺寸相对值之间的关系；

（2）弹体的头部类型对靶板的破坏模式具有很大的影响，尖头弹侵彻过程中靶板的破坏模式为花瓣开裂，靶板破坏前所处应力状态基本为拉伸状态；平头弹体侵彻过程中靶板破坏模式为剪切冲塞，破坏前所处应力状态为剪切状态。因此不同弹体头部类型侵彻计算中失效应变取值存在一定的差异。

文中以本课题组开展的战斗部侵彻试验为依据，具体见参考文献[14]：

（1）试验类型一：战斗部为平头战斗部，壳体材料为高强度高硬度30CrMnSi，炸药与引信材料采用PPS 塑料替代，战斗部弹径为92 mm，弹长为242 mm，壳体质量为2.86 kg，填充物质量为1.66 kg，总质量为4.52 kg。靶板材料为Q345B，尺寸为1000 mm×1000 mm，板厚为15 mm。战斗部入射速度为277 m/s，穿出速度为163 m/s。

（2）试验类型二：战斗部为尖头战斗部，壳体材料为高强度高硬度30CrMnSi，炸药与引信材料采用PPS 塑料替代，战斗部弹径为92 mm，弹长为276 mm，壳体质量为3.21kg，填充物质量为1.45 kg，总质量为4.66 kg。靶板材料为Q345B，尺寸为1000 mm×1000 mm，板厚为8 mm。战斗部入射速度为208 m/s，穿出速度为185 m/s。

依据Q345B钢断裂力学性能试验拟合JC本构模型及失效模型，对于JC本构模型，表达式为

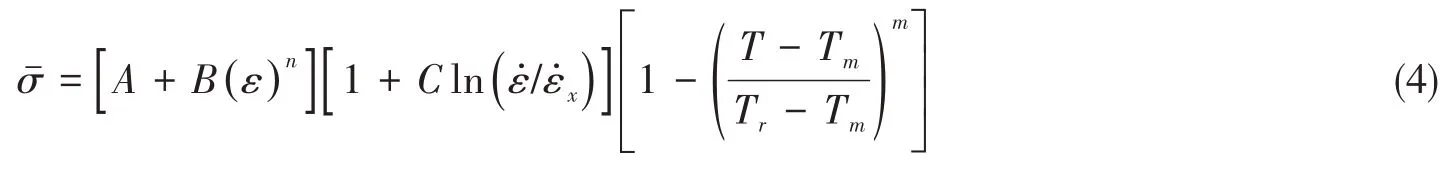
后文计算中A取360 MPa，B取300 MPa，n取值0.547，C取值0.046。

对于JC失效模型，表达式为

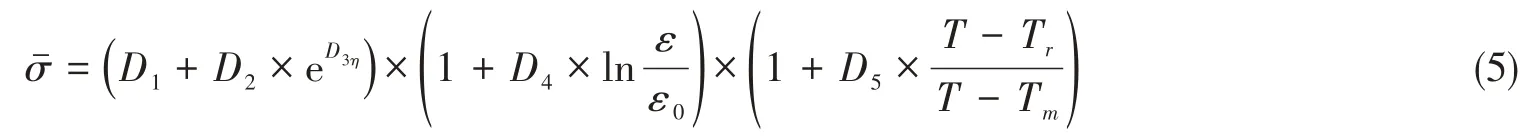
式中，D1取-0.091，D2取1.5362，D3取-0.091，由于未开展应变率效应、温度效应对失效应变影响力学性能试验，且考虑到二者影响相对较小，因此计算中D4、D5均取为0。后文计算中JC本构参数、JC失效参数取值保持一致。

为得到适用于大质量弹体侵彻靶板失效应变取值与网格尺寸之间的关系，针对每一种网格尺寸下的弹靶计算模型，分别采用不同α系数对应的失效应变，文中依次取α值为1.0、0.75、0.5、0.25 和0.1，通过不断尝试，摸清弹靶穿甲仿真中网格尺寸与失效应变之间关系。

图8 依次表示的是平头战斗部、尖头战斗部剩余计算值与网格尺寸之间的关系。针对平头战斗部，对于单元尺寸为3 mm、2 mm 和1 mm 的弹靶模型，失效应变缩放系数依次取α=0.38、α=0.52、α=1可获得与试验剩余速度一致的结果；针对尖头战斗部，对于单元尺寸为3 mm、2 mm和1 mm弹靶模型，失效应变缩放系数依次取α=0.3、α=0.52、α=0.97可获得与试验剩余速度一致的结果。由此可看出，当弹径与单元尺寸的比值为50 左右时，失效应变可取材料真实应变的一半（缩放系数取0.5）；当弹径与单元尺寸的比值为100 左右时，失效应变可直接取材料真实应变。国外Borvik、Iqbal、Gupta、Wierzbicki 等[7-8]公开发表的文献以弹丸、破片为研究对象，通过对比不同网格尺寸下仿真计算结果与试验结果，同样可发现当弹径与单元尺寸的比值控制在100以上时，直接采用试验获取的失效应变值与仿真计算吻合最好，这进一步验证了本文的结论。

图8 战斗部剩余速度与网格尺寸之间关系示意图Fig.8 Relationship between the residual velocity of the warhead and the element size

3.2 冲击载荷下方板仿真计算

方板等简单结构是开展冲击动力学研究的重要研究对象，相关方面开展的研究较多。仿真分析中方板结构通常采用实体单元进行模拟，冲击载荷作用下方板的撕裂破坏模拟与材料失效应变的取值存在很大的关系。考虑到方板撕裂过程中通常会形成较为明显的颈缩现象，本节主要从板厚角度出发，建立材料失效应变取值与板厚/单元尺寸之间的比值关系。

以本课题组开展的落锤冲击试验为依据，具体见参考文献[15]，冲击锤头表面为球形状，半径为300 mm，长度方向尺寸为300 mm，宽度方向尺寸为210 mm，材料为45 钢，锤头通过螺栓与导向板、质量块等连接，下落过程中锤头整体质量为2024 kg，试验方板为Q345B 材料，尺寸为450 mm×350 mm，厚度为2 mm，方板四周与工装框架模型焊接固定，试验过程中方板的有效试验区域尺寸为350 mm×250 mm，见图9。试验结果为：当落锤高度h为400 mm 时，方板出现塑性变形；当落锤高度h为500 mm 时，方板边界出现撕裂。

同前文类似，依据开展的Q345B 钢断裂力学性能试验拟合得到JC 失效模型参数。仿真计算中Q345B 方板网格尺寸为1 mm，即厚度方向划分2 个单元。依据本文对不同网格尺寸下平板拉伸试件下的模拟结果，当板厚方向划分2个单元时，失效应变取值约为材料真实应变的0.3倍。

仿真计算表明：当失效应变取值为材料真实应变的0.3 倍时，落锤高度无论是400 mm 还是500 mm，方板均未出现撕裂；经不断迭代计算，当失效应变取值为材料真实应变的0.2 倍，落锤高度为400 mm 时，方板未出现撕裂，而当落锤高度为500 mm 时，方板边界出现撕裂，与试验结果吻合较好，如图10所示。

图9 冲击锤头与试验方板模型示意图Fig.9 Numerical simulation model of impact hammer and square plate

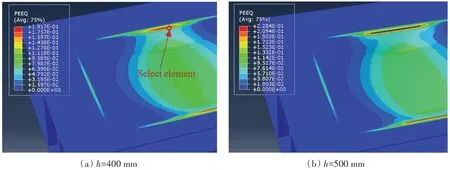
图10 不同锤高下方板的仿真计算结果示意图Fig.10 Simulation calculation results under different hammer heights

提取边界撕裂位置单元进一步分析落锤冲击下方板失效应变取值因素，选取单元位置见图10（a），图11表示的是该位置处单元应力三轴度、塑性应变变化过程，边界处单元塑性应变在累积的过程中单元应力三轴度基本处在[0.5 0.6]之间，高于平板拉伸试件过程单元所处的应力三轴度，因此失效应变取值较平板拉伸试件获取的0.3倍值更低，这与圆棒拉伸试件、缺口圆棒拉伸试件获取的规律一致。

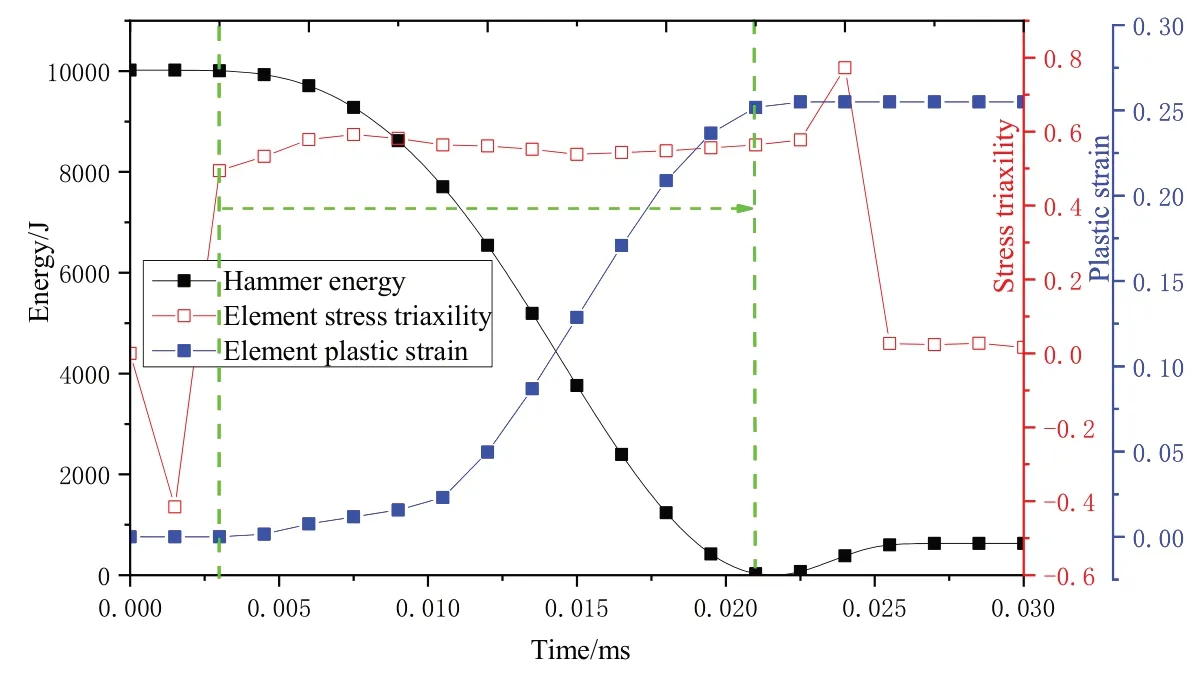
图11 单元应力三轴度及塑性应变变化示意图Fig.11 Variation of element stress triaxiality and plastic strain

综合可看出，当方板板厚方向划分为两层单元，且破坏模式主要为拉伸撕裂时，失效应变值可取材料真实应变的0.2倍。

3.3 舰船等复杂大尺度模型毁伤破坏仿真计算

舰船等复杂大尺度模型通常采用shell 单元建立，在进行水下爆炸载荷、空中爆炸载荷毁伤评估时，由于模型尺度较大，采用的shell 单元尺寸往往在几十毫米以上，撕裂破坏前局部集中塑性变形区域相对该网格尺寸所占比较小，此时建议失效应变可直接取材料颈缩之前对应的均匀应变。

以本课题开展的大尺度舱段模型水下近场爆炸试验为依据，具体见文献[14]。试验模型长度为15 m，宽度为3 m，高度为3.8 m，吃水1 m，模型主要分为5 舱段，其中中间舱段为试验舱，长度为3 m，两端依次为过渡舱、附加舱，见图12（a）所示。在垂直方向，模型中间试验段主要包含含水双层底、甲板、上层建筑等典型结构。试验段双层底高度为0.18 m，双层底结构板厚均为3 mm，舷侧外板板厚为3 mm，舷侧强肋骨、肋骨、纵桁采用T型加筋。加筋尺寸主要有两类：一类面板厚度为4 mm，长度为40 mm，腹板厚度为2 mm，长度为100 mm；另一类面板厚度为2 mm，长度为40 mm，腹板厚度为2 mm，长度为20 mm。各层甲板、上层建筑甲板厚度基本在2.5～3.5 mm之间，同样采用T型加筋进行加强，模型加工材料为Q345B钢，舷侧近距离爆炸试验在中国船舶科学研究中心爆炸水池中开展。

考虑到模型具有对称性，为提高计算效率，仿真计算中仅建立1/2对称模型，如图12（b）所示，利用Ls-Dyna软件中的ALE 算法进行水下爆炸分析，其中舱段模型采用shell单元，爆炸正对区域的网格尺寸为50 mm，空气、水域、炸药采用Eluer单元，流体结构间的相互作用采用关键字Lagrange-in-solid 定义，炸药为2.8 kg TNT，爆距为0.18 m。计算过程中Q345B 钢采用前文JC 本构模型参数，失效应变取光滑拉伸试件过程中对应的颈缩之前的最大均匀应变，取值为0.22。

图12 试验模型与仿真模型示意图Fig.12 Experimental model and simulation model

仿真与试验结果对比如图13 所示，试验后模型的变形毁伤区域基本集中在试验段横舱壁之间，其中舷侧外板形成较大破口，破口长度方向尺寸为202 cm，宽度方向为67 cm，舷侧破口基本处在肋位17#～23#，仿真计算中破口形状与试验结果较为类似，破口长度方向为152 cm，宽度方向为64 cm，舷侧外板破口基本集中在肋位17#～23#，破口尺寸相较试验结果较小的原因主要是ALE 算法中由于流体较大致使冲击波在传递过程中具有一定的弥散，从而导致作用舷侧外板的总能量相较而言减小了；试验中双层底上方2甲板发生较为明显的隆起变形，且在靠近舷侧爆炸区域出现局部撕裂，仿真计算中2 甲板亦出现较为明显的隆起变形，且靠近舷侧区域出现局部撕裂；试验中双层底靠近舷侧内底板格出现屈曲，并从板格边界撕裂，仿真计算中对应双层底由于板格屈曲较大出现撕裂。总体看来，采用本文建立的失效应变取值方法可较好模拟舰船等复杂大尺度模型的毁伤破坏计算。