海上浮体插销式连接结构极限承载能力及其统计特征分析

韩 越，郭建廷，刘磊磊，闻 静，李良碧

（1.江苏科技大学船舶与海洋工程学院，江苏镇江 212100；2.上海船舶研究设计院，上海 201203）

0 引 言

海洋环境十分复杂，浮体在服役期间不仅要承受风、浪、流等载荷，还要面临偶然性的载荷或灾害。连接结构作为多模块浮体中最薄弱的环节，受力形式复杂且受浮体运动影响大，其动力学性能直接决定多模块浮体波浪响应的频率特性、总体模态的动变形和运动安全性[1]。插销式连接结构作为铰接式连接器，其形式简单，仅通过面与面接触就能承载较大的外载荷，既能有效减小连接器的设计载荷，又能高度控制浮体运动方向[2]，且销轴能设置合理的外形，便于浮体结构在运动中对接，故在工程领域应用较广泛。因此，国内外学者一直致力于海上浮体连接结构特别是插销式连接结构的力学特性、极限强度以及安全可靠性等研究工作，并提出了多种以试验和数值计算为基础的连接结构力学机理分析手段和方法。

在连接结构载荷计算方面，Riggs 等[3]利用三维势流理论和格林函数法计算了移动海上浮体单模块的连接器载荷，并比较5个模块不相连、柔性连接以及刚性连接时的运动和连接器载荷，得出了连接器的布置形式对浮体的运动响应影响显著的结论；刘超等[4]比较了3种不同模型在7级海况作用下的连接器动力响应，研究了浅水效应对连接器动力特性的影响，得出了浅吃水超大型浮体的重心浮心差较大、稳性低、浮体间连接器的垂向载荷大的结论。在连接结构非线性计算方面，张浩等[5-6]以弹性接触方程为基础，采用罚函数方法，建立了连接器本体、钢轴与轴承座之间的接触关系，结合模型试验，验证了罚函数方法在模拟插销式连接器接触方面的可行性和准确性。在连接结构极限强度计算方面，张浩等[6]通过试验发现插销式连接器受纵向或垂向力时，轴承孔周边区域为应力集中的主要区域，且当荷载较大时，轴承孔周围会率先发生屈服破坏；张磊等[7]通过仿真分析发现铰制孔螺栓连接受力时孔边缘处存在应力集中，通过在剪切面处开卸荷槽或尺寸优化可有效缓解孔边缘的应力集中问题。此外，国内外学者对于连接结构极限强度的统计特征研究主要集中在屈服强度、板厚等材料属性的不确定性方面[8-12]，而接触摩擦力对结构极限强度的影响分析却较少，销轴构型为有锥度的情况也较少。

本文以一种含锥度的插销式连接结构为研究对象，基于罚函数法和准静态法，考虑轴销接触效应的影响，对该结构进行非线性强度计算，分析其失效模式和极限强度；同时，研究各类型参数特别是摩擦因子对结构极限承载能力的影响规律，最终形成一套考虑接触效应的复杂连接结构非线性极限承载能力及其统计特征分析方法。

1 理论基础

1.1 有限元分析中的非线性接触问题

接触问题是在外加荷载作用下，相互接触的物体产生局部变形和应力的问题。接触问题存在接触压力分布的非线性、接触区域变化非线性、摩擦引起的非线性以及材料塑性变形非线性等非线性特性。接触问题为单边不等式约束的平衡问题，其求解方法为反复迭代搜索准确的接触状态，具体平衡方程为式（1），变形协调方程为式（2）和式（3）[13]。

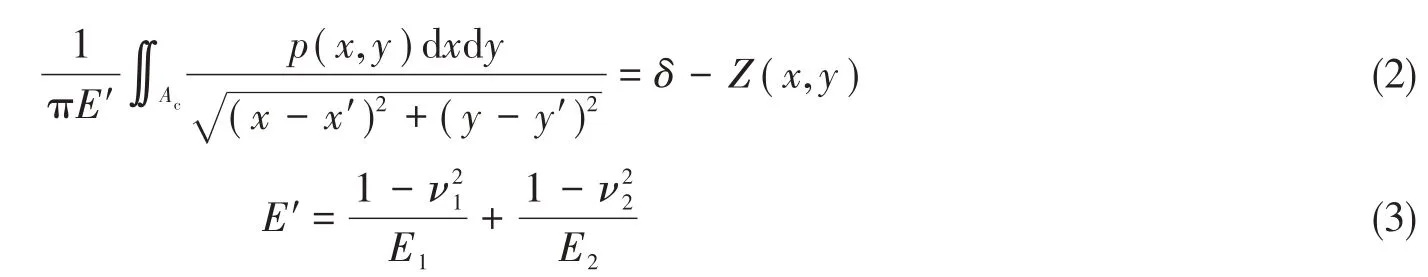
式中，Q为外载荷，p为接触应力，Ac为接触区域，δ为弹性趋近量，Z为初始间距，E1和E2为杨氏模量，ν1和ν2为泊松比。

国内外对于接触问题的理论研究已经有诸多相关成果，如Hertz弹性接触理论等。但这些接触理论只能求解一些较为简单的接触问题，简化假设较多，局限性较大。随着计算机技术的发展，以有限元为核心的CAE 仿真技术成为了解决接触问题的主流方法。目前，较为常用的接触计算方法有传递矩阵法、间隙有限元法、罚函数法和拉格朗日法等，本文采用罚函数法进行计算。

罚函数方法就是根据能量最小化原理，将接触问题通过寻求唯一接触状态变成系统势能最小化问题。当接触间隙大于等于0时，罚函数方程如下：

通过引入罚函数的附加泛函，可以将式（4）的约束极值化问题转化为下述的无约束极值化问题。通过选取适当大小的惩罚因子，可以达到较好的计算精度，同时避免病态方程的产生。

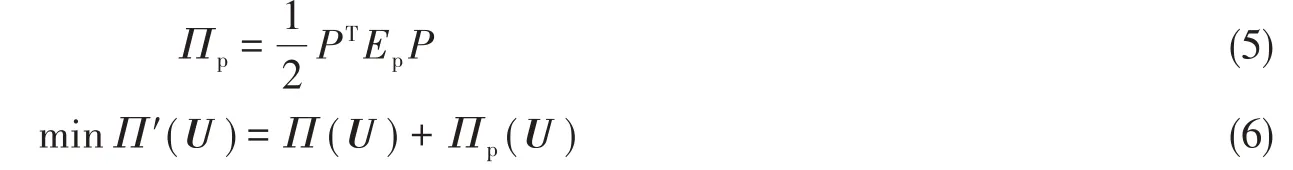
式中，Ep为惩罚因子，P为嵌入深度为系统势能，U为位移向量。

1.2 非线性有限元极限强度计算方法

非线性有限元极限强度计算中最常用和最有效的方法是弧长法和准静态法。本文采用准静态法计算连接结构的极限强度。准静态分析法是结构动态求解方法。通过缓慢动态加载来模拟静态问题，以结构非线性运动方程为基础求解极限强度。在求解过程中使用中心差分法进行显示时间累积，并依据上一载荷步力学条件计算下一步的力学条件，直到问题解决。

合理设置加载速度对准静态法求解至关重要，加载过快会使结果出现局部变形，载荷-位移曲线出现振荡，而过慢的加载会使计算时间增长。因此分析时，需要取多个不同加载速率进行比较，然后选定合适的加载速率。

1.3 试验设计的拉丁超立方设计方法

试验设计（design of experiments，DOE）分析方法是基于数理统计学理论建立的，用来合理而有效地获取信息数据，它在工程和科研领域有着广泛的应用。现行的试验设计方法多种多样，有必要结合实际问题选择一种合适的方法。目前拉丁超立方设计（Latin hypercube design,LHD）在实际工程中应用较为广泛，该方法可以以较少的试验来获得更多的信息，且拉丁超立方广泛分布的数据点保证了近似值的高精度[14]。

拉丁超立方设计由Mckay、Beckman 和Conovers 首先提出[12]。其原理就是在一个d维单位立方体Cd=[0,1]d中选出n个点，先把每一维坐标区间[0,1]等分为n份，并用记号i标记小区间，用(π1j,π2j,…,πnj)记第n维坐标的n个标号(1,2,…,n)的一个随机排列。又设这d个随机排列相互独立，得到一个n·d阶的随机矩阵：

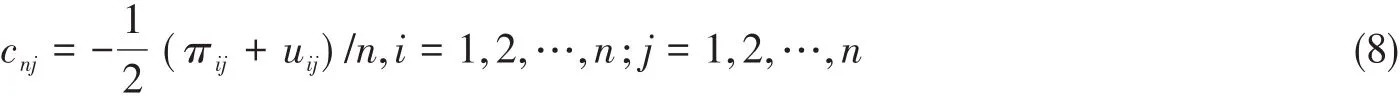
式中，uij是与π独立的上均匀分布的一个蒙特卡洛抽样样本。这样选取的n个点ci=(ci1,ci2,…,cin),i= 1,2,…,n为一个拉丁超立方抽样样本。该抽样样本具有良好的散布均匀性和代表性，加之它是随机的，搜索能力更强，可以以较少的试验来获取更多的新信息，且拉丁超立方广泛分布的数据点保证了近似值的高精度。

2 海上浮体插销式连接结构初步设计

本文初步设计了一种插销式海上浮体连接结构，设计载荷为2500 t。如图1 所示，该连接结构通过销轴与轴承座的插拔实现浮体的连接与解脱，浮体模块可以绕销轴相对转动，即释放绕Y轴旋转的自由度。如图2～3 所示，一侧轴承圈设计有1：100 锥度，各轴承内圈边缘含有半径为30 mm 的圆角，两轴承距离为80 mm；轴销最小直径为800 mm，最大直径为814 mm，销轴与轴承孔之间有1 mm的间隙。

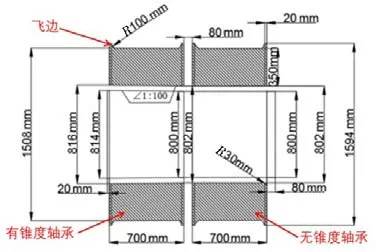
图2 连接结构几何尺寸图Fig.2 Dimensions of the connection structure

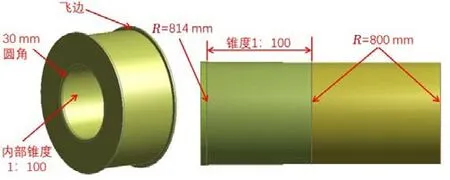
图3 有锥度轴承、销轴三维图Fig.3 3D drawing of taper bearing and pin shaft

3 海上浮体插销式连接结构极限承载能力分析

3.1 有限元模型

选取插销式连接结构的关键承载部位即轴承和销轴作为分析对象。依据有限元建模特点，轴承和销轴均以体单元模拟。如图4所示，有限元模型共有单元51 894个，节点230 747 个。综合考虑计算收敛性和计算效率，在销轴与轴承孔边缘接触处选取尺寸为30 mm×30 mm×30 mm的网格进行细化。

图4 有限元模型Fig.4 Finite element model

3.2 结构约束、加载方式及材料属性

轴承和销轴选取结构钢材料（弹性模量为2.0×1011N/m2,密度为7850 kg/m3，泊松比为0.3），采用屈服强度为250 MPa 的应变硬化曲线。基于相关浮体研究资料[1-6]和设计方案，本文对有锥度轴承的两个飞边设置刚性约束，对无锥度轴承的两个飞边以Remote Force 方式沿X方向施加设计载荷2500 t。由于插销式连接结构为环形对称结构，该约束、加载方式能有效模拟纵向受力过大和垂向受力过大的组合工况。

3.3 插销式连接结构静强度有限元分析结果

采用有限元ANSYS/Workbench软件中的静态分析模块进行计算。在销轴和轴承间设置两组摩擦接触对，设定初始间隙为1 mm，允许销轴在轴承内滑移和转动，选用罚函数接触算法[3]，罚函数因子取0.1，摩擦因子取0.2[8]。计算结果如图5、图6所示，插销式连接结构整体von-Mises应力不大，最大应力位于有锥度的轴承上，具体在轴承内圈边缘，约为264 MPa；销轴最大应力约为260 MPa，位于有锥度部分和无锥度部分的过渡段。结构最大应力处于塑性阶段，主要为销轴受剪力弯曲后与轴承内圈挤压从而变形失效，销轴和轴承最大应力几乎相等。

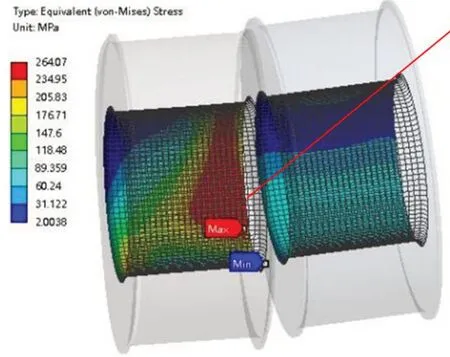
图5 轴承von-Mises应力Fig.5 von-Mises stress of bearing

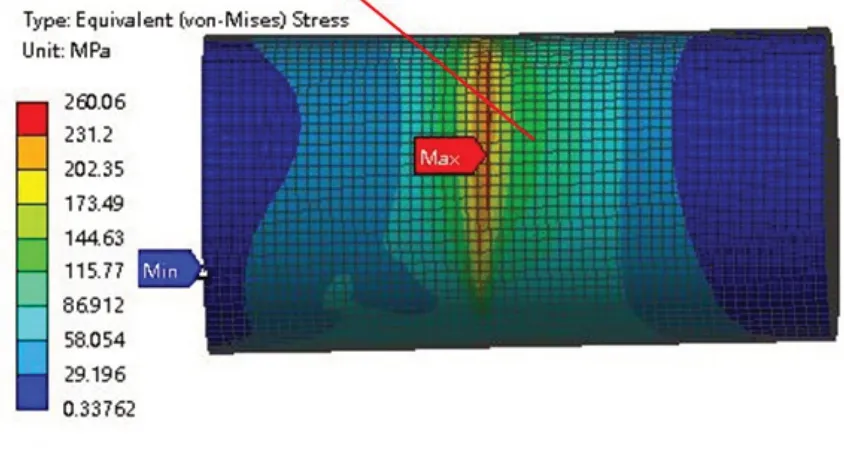
图6 销轴von-Mises应力Fig.6 von-Mises stress of pin shaft

3.4 插销式连接结构极限承载能力分析

考虑到几何非线性、材料非线性以及接触非线性，对图4 所示的有限元模型分别选取屈服强度σ1=250 MPa 和σ2=355 MPa 的应变硬化曲线[15]进行分析。设定与本文第3.2 节相同的约束方式，并将加载方式改为强迫位移。借助ANSYS/Workbench 有限元软件，基于非线性有限元加载准静态法和罚函数接触分析法，对插销式连接结构进行极限强度分析。

图7 为插销式连接结构不同屈服强度材料极限承载力的载荷-位移和应力-位移曲线。由图7 可知：当插销式连接结构材料σ1=250 MPa 时，极限强度为269 MPa 左右，能承受的极限载荷约为3097 t；而当σ2=355 MPa 时，极限强度为380 MPa 左右，能承受的极限载荷约为4386 t。该结构最先失效位置与静强度分析结果较为一致，即位于有锥度的轴承内圈边缘附近，因此不同屈服强度材料之间的结构极限承载能力有较大区别。

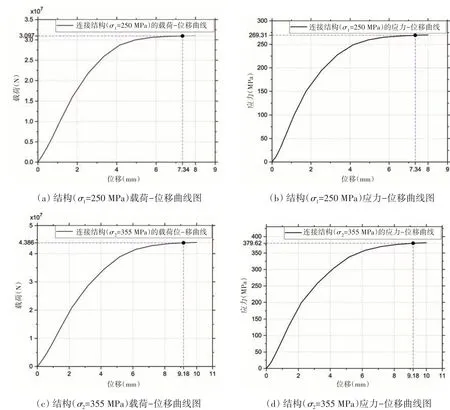
图7 插销式连接结构极限承载力结果Fig.7 Results of ultimate bearing capacity of bolt connection structure

4 插销式连接结构极限强度统计特征分析

4.1 摩擦因子不确定性对插销式连接结构极限承载能力的影响

查阅文献[8]可知，接触面间摩擦因子大小对连接结构受力有影响，插销式连接结构摩擦因子依据钢材属性、是否涂润滑油等情况取值，范围为0.1～0.35。为更好地模拟摩擦因子的实际情况，本文将摩擦因子分为有锥度侧和无锥度侧两部分，每部分进行独立的高斯分布抽样，平均值取0.2，变异系数取0.05，并采用LHD 方法对抽样后参数进行试验设计，着重分析摩擦因子对极限承载能力的影响规律。借助ANSYS 软件中的APDL 语言实现参数化，进行抽样试验10 000 次，拟合结果并分析。图8 为插销式连接结构极限承载力随摩擦因子变化的趋势，表1和表2分别为该变化趋势的极值统计和分布拟合结果。

由图8 和表1 可以看出，插销式连接结构摩擦因子的变化对极限载荷影响较小，而对结构极限强度影响较大。屈服强度为250 MPa时，连接结构由摩擦因子引起的极限强度变化值为39.38 MPa，相对极差达15.5%；当屈服强度为355 MPa时，该变化值为43.72 MPa，相对极差达11.4%。通过分布拟合和假设检验，摩擦因子变化引起的极限强度变化服从对数正态分布，如表2所示。

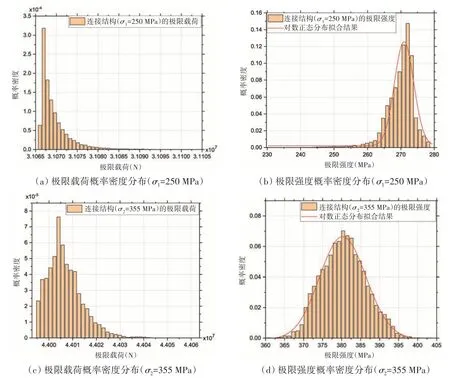
图8 插销式连接结构极限承载力概率密度分布Fig.8 Probability density distribution of ultimate bearing capacity of bolt connection structure

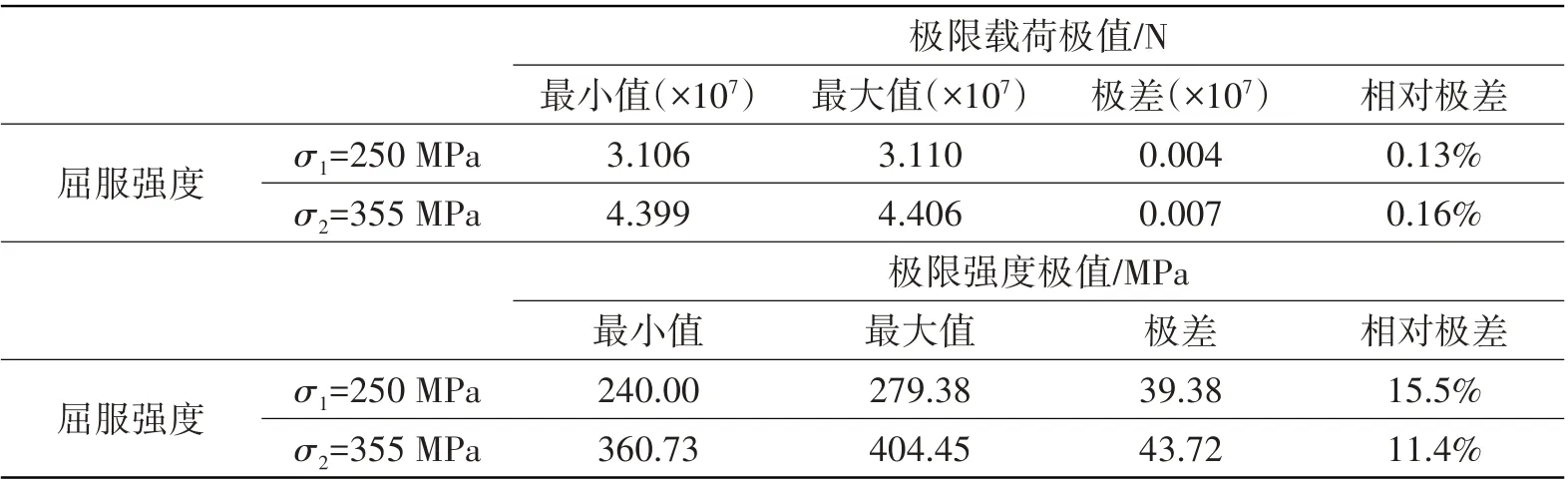
表1 插销式连接结构承载能力极值统计Tab.1 Statistics on extreme value of bearing capacity of bolt connection structure

表2 极限强度分布拟合结果Tab.2 Fitting results of ultimate strength distribution

图9 为插销式连接结构摩擦因子的灵敏度分析。从图9 可以看出，摩擦因子和极限强度负相关，即摩擦因子波动会引起结构极限强度波动，摩擦因子越大，结构极限强度越小，有锥度轴承处的摩擦因子对极限强度变化起主导作用，主导能力随材料屈服强度增大而增大。

4.2 屈服强度不确定性对插销式连接结构极限承载能力的影响

影响结构极限强度的客观不确定因素还有材料屈服应力和弹性模量等多种因素。材料的统计参数需要通过大量的钢材样本试验得到，国内外不同学者也对此进行了大量研究，Mansour 等通过分析300个试样得到结构弹性模量的变异系数约为0.031，均值为2.06×1011Pa[16]。吴东伟在Mansour 的基础上进行了完善总结分析，计算得到弹性模量均值的加权平均值为2.06×1011Pa，变异系数为0.025，同时通过对钢材屈服强度的统计分析，取材料屈服应力变异系数为0.08，弹性模量和屈服强度符合高斯分布或对数分布统计分析[17]。所以本文在第3.1 节的基础上，增加了弹性模量和屈服强度的不确定性分析，具体参数化变量和抽样分布见表3。

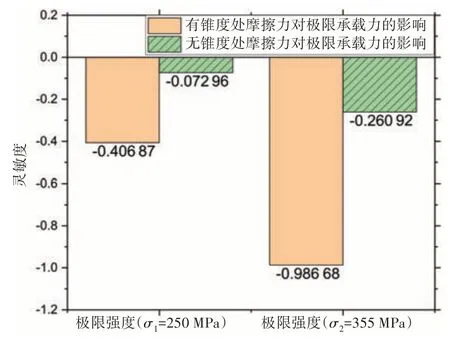
图9 摩擦因子灵敏度分析Fig.9 Sensitivity analysis of friction factor

表3 材料属性及摩擦因子抽样分布Tab.3 Material properties and friction factor sampling distribution

图10为插销式连接结构极限承载力不确定性分析结果，表4和表5分别为该结果的极值统计和灵敏度分析。从图10 和表4 可以看出，极限强度和极限载荷变化服从高斯分布。当σ1=250 MPa 时，极限强度均值为268 MPa 左右，能承受的极限载荷均值为3080 t 左右；而当σ2=355 MPa 时，均值分别提升至379 MPa和4360 t左右。表5的灵敏度分析显示，不同参数化变量对于结构极限承载力变化有不同的解释度，其中屈服强度的解释度高达0.99，有锥度处摩擦因子解释度为-0.03，即插销式连接结构极限承载能力受屈服强度影响较大，受有锥度处摩擦因子影响较少，不受无锥度处摩擦因子和材料弹性模量大小的影响。

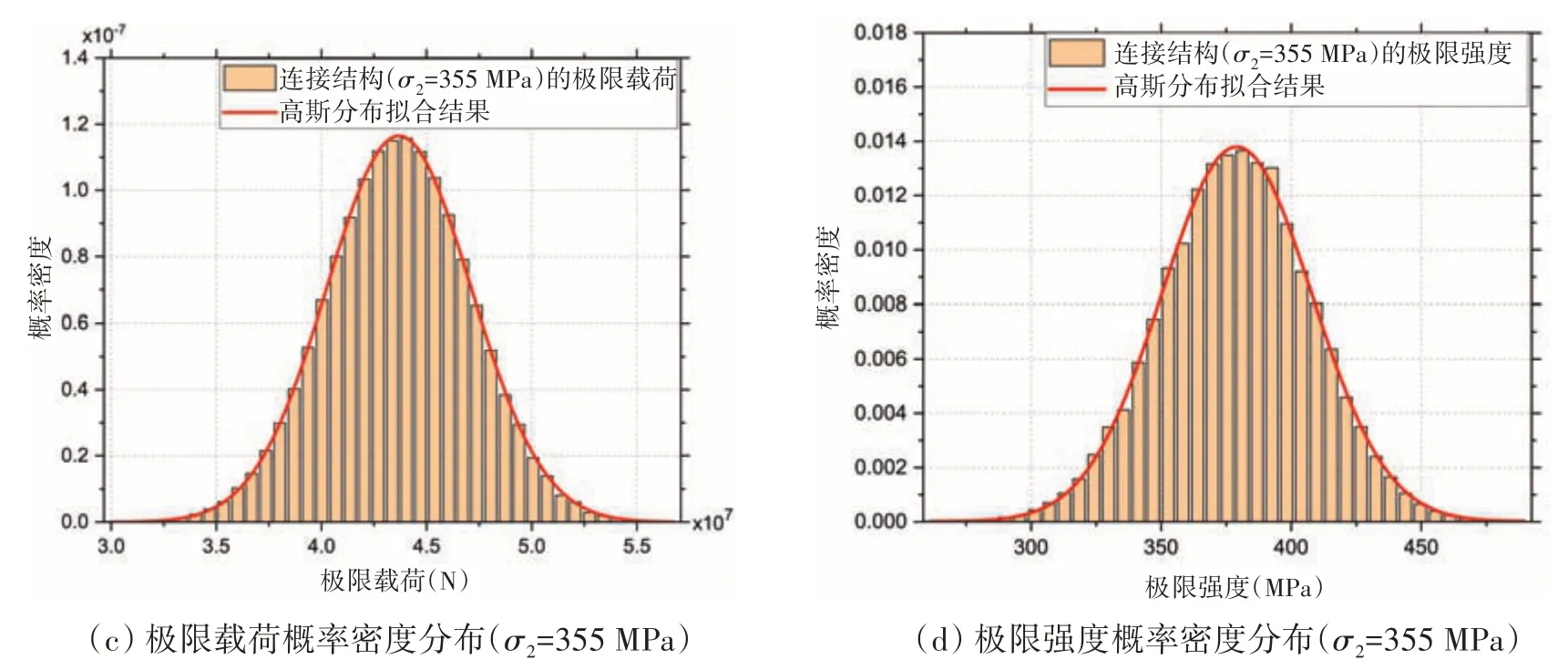
图10 插销式连接结构极限承载力不确定性分析结果Fig.10 Uncertainty analysis results of ultimate bearing capacity of bolt connection structure

表4 插销式连接结构极限承载能力分布拟合Tab.4 Distribution fitting of ultimate bearing capacity of bolt connection structure

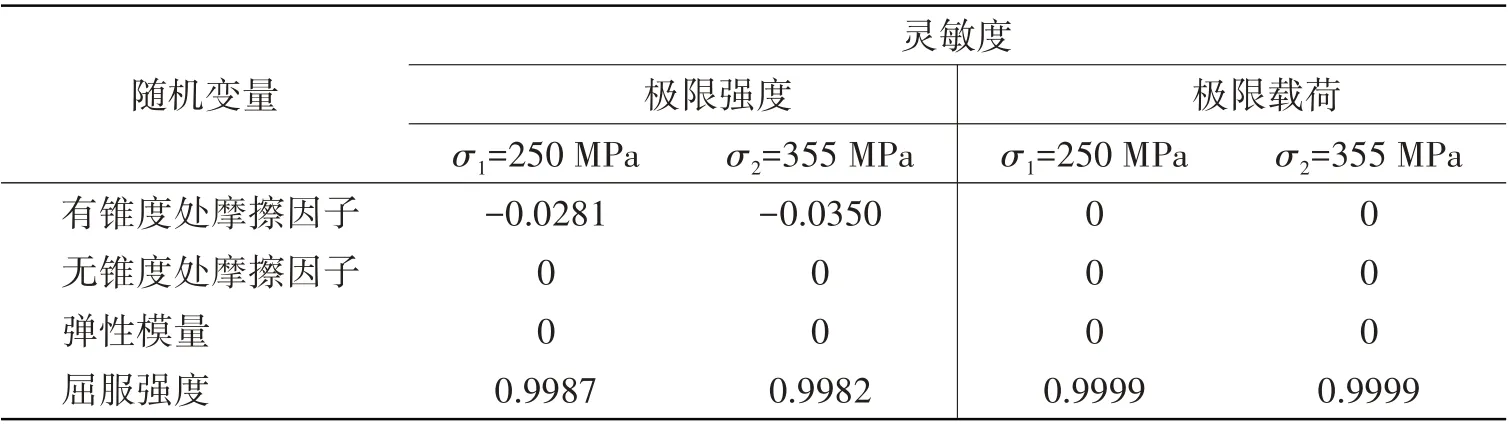
表5 插销式连接结构材料属性及摩擦因子灵敏度分析Tab.5 Sensitivity analysis of material properties and friction factor of bolt connection structure

5 结 论

本文初步设计了一种含锥度的插销式连接结构，基于罚函数法和准静态法，考虑轴销接触效应的影响，对该结构进行非线性强度计算，分析其失效模式和极限强度，并将摩擦因子和材料属性参数化，研究各类型参数对该结构极限承载能力的影响，最终形成一套考虑接触效应的复杂连接结构非线性极限承载能力及其统计特征分析方法。主要研究结论如下：

（1）通过连接结构应力分布分析表明，本文设计的插销式连接结构在设计载荷作用下，有锥度轴承孔边缘内圈为应力集中的主要区域，轴承孔周围会率先发生屈服破坏。主要失效模式为轴承传递压力与摩擦力迫使销轴弯曲后与有锥度轴承挤压从而变形失效。

（2）摩擦因子对插销式连接结构极限强度的影响呈对数正态分布，相对极差达15.5%，摩擦因子越大，极限强度越小。有锥度轴承内圈摩擦因子波动是引起结构极限强度波动的主要原因，且材料屈服强度越大，波动越明显。

（3）综合材料属性和摩擦因子对插销式连接结构极限承载能力的影响呈高斯分布，材料屈服强度是最主要的正相关影响因素，即屈服强度越大，结构承载能力越强。