基于人工智能的三维结构全局应力求解方法研究

2023-03-01胡嘉骏汪雪良徐业峻王子渊

船舶力学 2023年2期

张涛，胡嘉骏，汪雪良，徐业峻，郑重，王子渊

（1.中国船舶科学研究中心，江苏无锡 214082；2.深海技术科学太湖实验室，江苏无锡 214082；3.中海油能源发展股份有限公司采油服务分公司，天津 300452；4.大连船舶重工集团装备制造有限公司，辽宁大连 116052）

0 引言

为保障船舶与海洋装备在运行状态下的结构安全性，结构健康监测技术（structure health monitoring,SHM）应运而生。它利用各类传感器对结构力学参量进行采集，基于预先设计好的算法，评估结构的服役情况、可靠性和耐久性等，在结构处于异常时触发预警信号，为结构的维修、养护与管理决策提供依据和指导[1]。然而，在实际工程应用中，由于有限数量的传感器无法覆盖可能发生结构失效的全部区域，导致SHM系统仅能自主实现较初级的安全警示功能。

为此，研究人员开展了大量研究，探索基于离散测点重构结构全场应力的方法，希望在装备运营状态下获取更多的结构细节。1995 年Haugse 等[2]首次提出模态法，通过结构的模态坐标作为整体结构模态的权重值，进而得到应变场到位移场的转化矩阵，再通过离散的应变测点重构结构变形，其核心思想是将结构变形视为各阶模态的线性组合，重构精度受模态分析精度影响较大，通常用于含损结构的损伤识别；Ko[3]等于2007 年首次提出Ko 位移理论，该方法基于典型的伯努利-欧拉梁理论，假设每个小段梁的弯曲变形仅由弯矩引起，建立弯矩与应变之间的关系，通过对测得的轴向应变进行两次积分获得梁结构的变形，该方法的局限性在于只适用于单方向的结构变形重构；Tessler（2003）[4]首次提出“逆有限元法(iFEM)”，该方法将结构拆分为一维、二维和三维单元，通过在指定位置布置应力传感器进行离散求解，再组装为整体矩阵，重构获得全局应力场；Oterkus[5]等运用iFEM 法对一艘倾覆的散货轮平行中体应用iQS4 单元开展了全局应力和弯曲计算，证明了iFEM 技术在散货船上的实用性。国内也有很多学者基于iFEM 法对梁、框架、板壳等结构变形重构进行了研究[6]。然而，在对复杂弯曲结构进行iFEM 分析时，需要基于现有逆壳单元生产更精细的网格，导致iFEM 重构复杂弯曲结构应力场的代价依然昂贵。2019年，彭茄芯[7]等以体育馆钢结构为分析对象，通过结构关联分析，建立了实测点与待估计点的映射关系，对应力场的重构提供了新思路；2021 年，张宏[8]针对油气管道应力监测数据，采用BP神经网络与粒子群优化算法，建立了管道沿线二维应力分布机理模型，并通过实例验证了模型的准确性，该方法的优势在于测点数量少且求解速度快。

本文针对船舶与海洋装备中有限数量的应力测点难以把握结构全局应力状态的问题，提出运用人工智能方法求解三维结构全局应力，重点阐述测点选取的理论依据与神经网络模型架构流程，并通过仿真计算数据和实尺度模型试验数据证明了该方法的可行性与求解精度，实现对复杂结构应力分布状态的实时可视化呈现，切实提升SHM设备的实用性。

1 三维结构有限元响应相关性分析方法

依据有限元理论将整体结构划分为一定数量的有限单元，当外载荷发生变化时，对于一维、二维结构，有限单元的应力变化整体上呈现一定的相似性和规律性；而对于三维空间结构，有限单元的应力变化呈现复杂分布，并且结构越复杂，有限单元整体规律性越弱。本文拟基于有限单元对载荷响应的相关性，将三维结构整体拆分为若干子集，这些子集中的有限单元对载荷的响应具有相似性和规律性，通过子集中的特征点求解三维结构全场应力。

将三维结构整体划分为m个有限单元，在n个载荷步作用下，结构响应矩阵X为

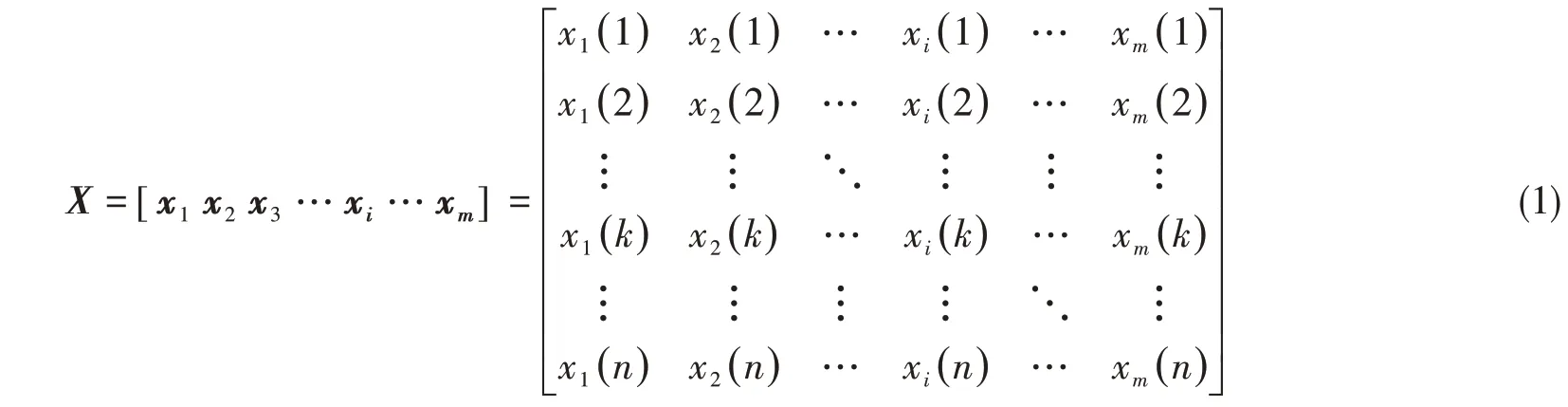
式中，编号为i的有限单元在n个载荷步作用下的结构响应为xi，

式中，i=1,2,…,m。分析三维结构中任意两个有限单元xi和xj在同一加载步的响应相似程度，可采用协方差Cov( )xi,xj表示：

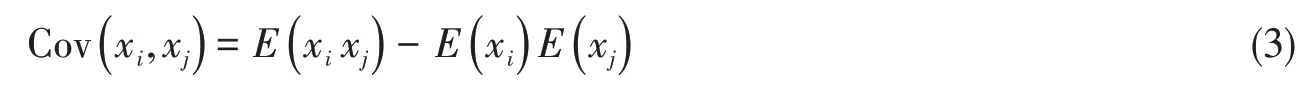
式中，E(xi)与E(xj)分别为两个实随机变量xi与xj的期望值。考虑到两个变量为不同的量纲时，它们的协方差在数值上表现出很大的差异。为此引入无量纲相关性分析计算方法，例如Pearson 相关系数，见公式（4）:

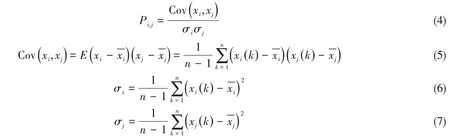
式中，σi是编号为i的有限单元在n个载荷步下响应值的方差，σj是编号为j的有限单元在n个载荷步下响应值的方差是编号为i的有限单元在n个载荷步下响应值的均值是编号为j的有限单元在n个载荷步下响应值的均值。则任意两个有限单元xi与xj之间的关联矩阵P为

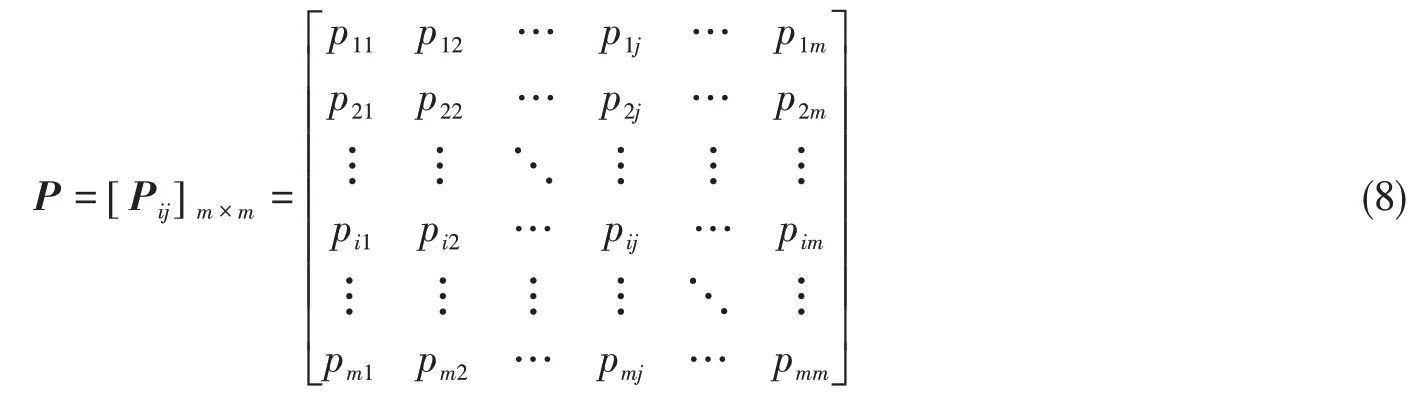
相关系数p的取值范围为[-1,1]，如图1 所示。当p=1 时，xi与xj为完全正相关；当p=-1 时，xi与xj为完全负相关。p的绝对值越大，相关性越强；p越接近于0，相关性越弱。

通常取pij＞0.95，认为xi与xj具有显著的相关性。将三维结构中对载荷反馈具有明显相关性的有限单元归为同一集合，则m个有限单元形成的三维结构整体S可拆分为k个子集Ti，

式中，i=1,2,…,k。分别从Ti中筛选具有代表性的有限单元vi，组成特征单元集合V={ }v1,v2,…,vi,…,vk。基于神经网络可以建立特征单元集合V和与其具有显著相关性有限单元与S之间的求解关系，在特征单元布置应力传感器即可求解结构全局应力数据。

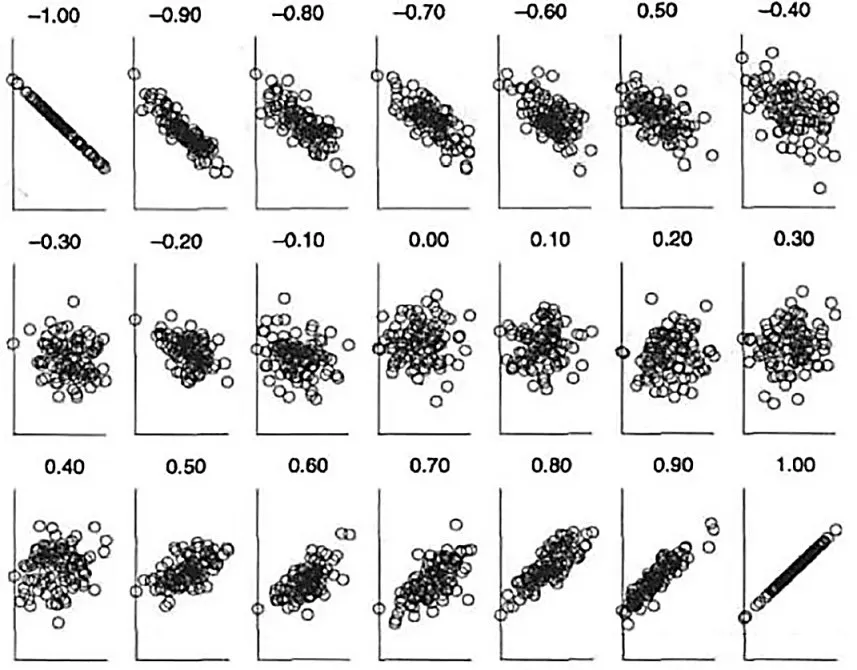
图1 相关系数与相关程度示意图Fig.1 Schematic diagram of correlation coefficients and correlation degrees

2 三维结构应力场求解神经网络架构方法

2.1 人工神经网络原理

人工神经网络是通过训练大量的隐藏参数（隐藏层），以实现从输入变量到输出变量的映射，来拟合复杂现实规律的人工智能算法，单网络结构图如图2所示。本文将特征单元集合V的应力值作为神经网络输入层，将整体结构所有有限单元应力值集合X作为输出层，以可信的输入与输出数据作为训练样本集建立监督学习网络，神经网络学习系统根据已知输出与实际输出之间的差值（误差信号）调节系统参数，最终建立特征点与整体结构应力场的匹配关系模型。

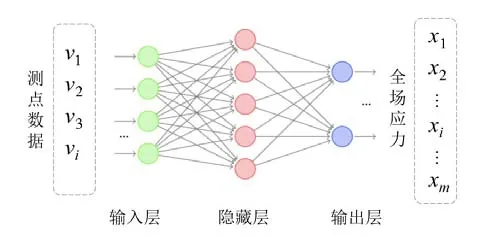
图2 简单全局应力求解神经网络结构图Fig.2 Simple neural network for solving global stress

2.2 初始应力场人工智能模型构建方法

由于无法通过实测手段获得三维结构应力场数据，选择有限元仿真计算数据作为训练样本，建立初始应力场神经网络模型（下称“初始模型”），流程如图3所示。

图3 初始模型构建路径Fig.3 Technical path of building initial model

将样本数据划分为不相交的三部分：训练集、校验集和测试集。其中，训练集用于对网络进行训练，以使网络能够具有全场应力的求解能力。从训练集中，将所有有限单元的响应值设为输出（即“目标数据”），通过前向传播的方式将特征单元数据作为输入，建立多层级的加权求和矩阵，计算得到输出预报数据；当预报数据与目标数据差值不满足误差要求时，再运用反向传播算法，调节系统参数，最终建立特征单元与全场应力的求解模型。校验集用于判断当前网络对全局应力场的求解能力，评估模型训练过程中的收敛情况，作为是否结束网络训练的判断依据。测试集用于评估训练完成的模型在应力求解任务中的性能表现，量化模型对全局应力预测精度的分散性。

2.3 应力场人工智能模型修正方法

基于仿真计算数据建立的初始模型经过修正后才能部署于实体结构，原因在于：（1）仿真计算的材料属性、边界条件、网格划分、载荷模拟与真实状态存在微小差距；（2）实际测点位置可能与特征单元位置存在几何上的定位误差。

如图4 所示，基于传感器实测数据通过监督学习修正初始模型，将测点分为三类：长期测点、修正点与精度考核点。其中，长期测点为应力场人工智能模型的输入层，输入初始模型求解全局应力；在实体结构应力较大的区域随机选取若干修正点，将初始模型预测值与修正点实际测量值比对，通过半监督学习在初始模型的输出层外添加修正矩阵，建立应用于实体结构的、最终的应力场人工智能模型（下称“最终模型”）；最后，在高应力区域任意选取验证点，用以评价最终模型精度。

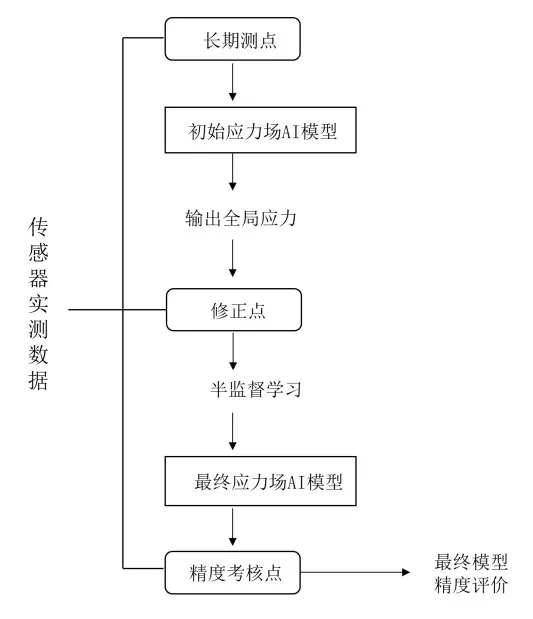
图4 初始模型修正路径Fig.4 Correction process of initial model

3 海洋平台连接器应力场求解初始人工智能模型开发

3.1 连接器结构简述

某海洋平台由两个半潜浮式平台组成，主平台与辅平台之间通过插销连接，如图5所示。在极端海况下销轴与连接器承受较大的剪力[9-10]，需实时评估结构的安全性。本研究通过在连接器结构表面布置应力传感器，即时求解连接器结构应力云图，从而识别高应力位置与大小，评估连接器结构安全性。连接器分为单耳与双耳结构，如图6 所示。选择单耳连接器为研究对象，该结构为复杂三维结构，包含曲面，且有三层舱壁，中间舱壁含减轻孔，如图7所示。

图5 某海洋平台的连接器结构Fig.5 Connector structure of the offshore platform

图6 单耳与双耳连接器结构Fig.6 Single ear and double ear connector structure

图7 连接器结构内舱壁图Fig.7 Inner bulkhead of connector structure

3.2 仿真计算数据样本

销轴剪力可360°施加于连接器结构，因此开展3600 组弹性阶段计算工况，含36 个载荷方向（每10°为一个方向）下的100 个分层载荷，将全部载荷工况下所有有限元应力数据作为样本数据，随机分组成训练集（2400组）、校验集（600组）和测试集（600组）。

3.3 相关性分析与特征单元筛选

通过Pearson 相关系数对连接器结构有限元进行相关性分析，依据公式（4）～（8）得出有限单元关联矩阵P，特征单元筛选步骤如下，如图8所示。

（1）从整体结构中剔除无法安装传感器的有限单元。将剩余的有限单元按照应力绝对值从大到小排序，应力绝对值越大说明该有限单元对外部载荷越敏感，在该位置布置测点有利于感知外部载荷和结构响应的微小变化。

（2）将Si中应力绝对值最大的有限单元作为特征单元vi，其中i为重复次数。依次计算Si中其它单元yj与vi的相关性系数ρij，j={ }1,2,…,m，m为Si中元素的个数。若ρij＞0.95，则将y加入集合Ti。

（3）将Si中与Ti重复的单元删除，得到剩余的单元集合D。

（4）重复步骤（2）,（3），直至剩余单元集合D中个数等于0，则完成选取。

至此，从30 858 个有限元中找出50 个特征单元，如图9所示，即连接器结构可拆分为50个子集。

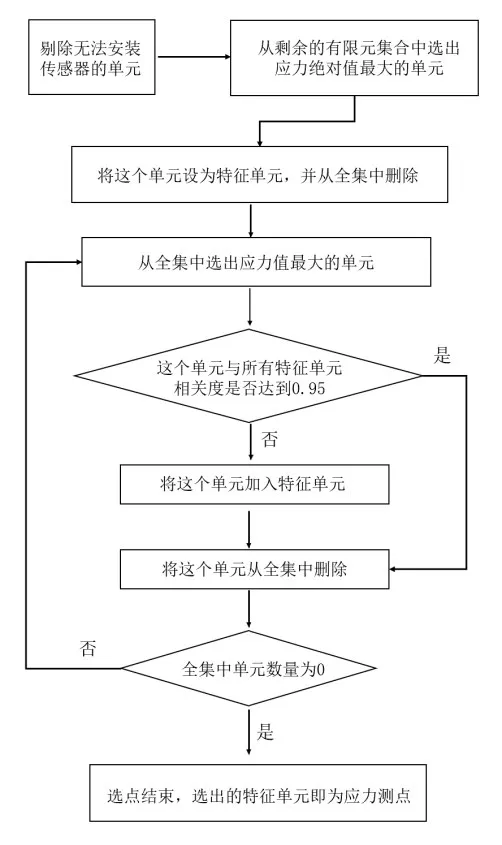
图8 特征单元筛选流程Fig.8 Selection process of the feature finite elements

图9 筛选出的50个特征单元编号Fig.9 Identifier of the selected 50 feature finite elements

3.4 测点数量优化

将50 个特征单元按照应力幅值由大至小排序，并统计各特征单元的相关有限单元数量，如图10所示。结果表明，与50个特征单元相关的有限单元总和为220 905，远超出有限单元的总和30 858，说明50个子集中存在多个交集，可以使用更少的特征单元求解全场应力。

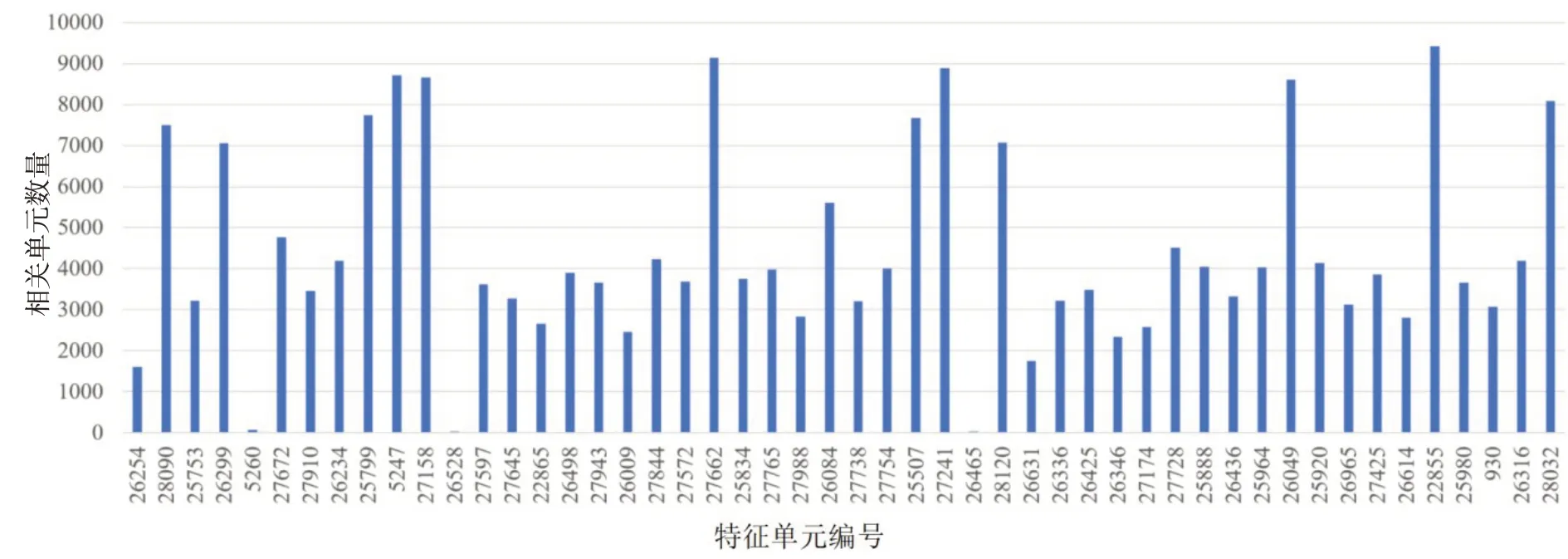
图10 各特征单元的相关单元数量（按照载荷敏感性强到弱排序）Fig.10 Number of related units of each characteristic elements(Load sensitivity from strong to weak)

按照幅值由大到小，分别选取5、10、15、20、25、30、40、50 个特征单元为输入变量，训练应力求解神经网络模型，分析不同数量的特征单元对应力场求解精度的影响，结果如图11所示。可观察到，随着选点数量的逐渐增加，计算精度逐渐提升，在选点数量为20 时，算法精度基本稳定。说明连接器结构中大多数有限单元与前20 个特征单元具有明显相关性，仅需20个特征单元即可满足连接器结构全场应力的求解需求。

3.5 神经网络优化

神经网络架构对全场应力的计算性能和计算精度存在影响，选择常用的四种神经网络构造（BP、CNN、RNN、DNN）开展试验，基于相同的输入点集、仿真数据构成的校验集以及收敛条件，BP为现在使用的优化过的标准网络模型，CNN 使用Pytorch提供的conv2d卷积层，RNN 序列大小为3，DNN 使用10层神经元。对比表1中AI算法与校验集中取得的精度最小值和最大值，比较不同网络模型的算法精度。

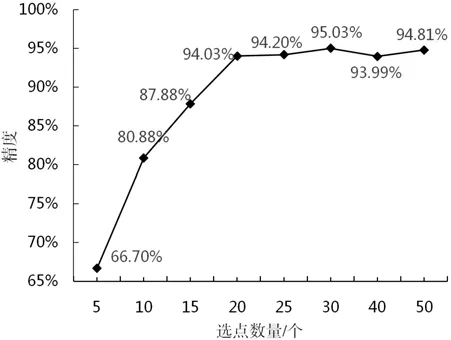
图11 特征单元数量对求解精度的影响Fig.11 Influence of the number of feature points on the solution accuracy

表1 不同神经网络架构求解精度比对Tab.1 Comparison of solution accuracy of different neural networks

通过观察表1 的实验结果可以发现，CNN 网络精度最低，基于BP 与RNN 网络模型方法预测出的点得到的效果略逊于DNN 网络，但DNN 和RNN 网络消耗的算力过多，见图12～13，且BP 网络求解精度相对稳定，综合求解精度以及计算速度，BP网络性能更优。

图12 BP神经网络求解过程Fig.12 Solving process of the BP neural network

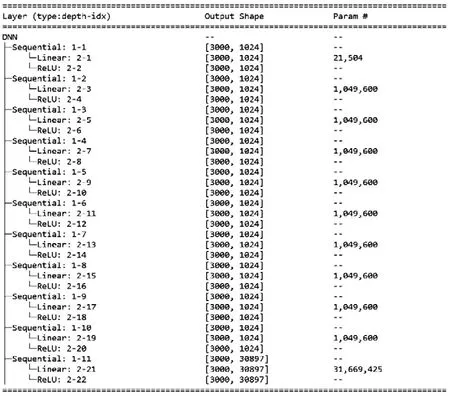
图13 DNN神经网络求解过程Fig.13 Solving process of the DNN neural network

3.6 神经网络收敛性分析

神经网络在训练过程中存在过拟合现象，根据有限元计算得到连接器结构仿真数据，图14 为使用BP 神经网络训练应力求解神经网络模型时不设置收敛判断的过拟合曲线，横坐标为训练轮次，纵坐标为精度。蓝色曲线为每训练200轮使用校验集验证的精度，红色曲线为每训练200轮使用测试集评估模型的精度。观察可知：

（1）随着训练轮次的增加，模型预测精度呈先上升，接着趋于平缓，最后急速下降的现象（即过拟合），有必要设计收敛规则；

（2）校验集和测试集在精度上的表现趋势一致，说明了校验集能有效提供模型性能的近似评估。

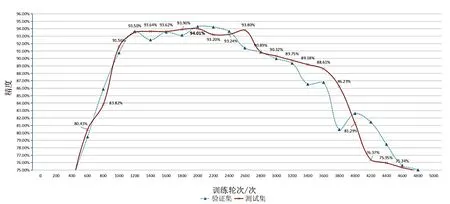
图14 应力求解神经网络模型训练过程Fig.14 Training process of the neural network model

因此，在训练连接器结构应力场求解神经网络时，应设置如下收敛规则：当校验集验证模型精度出现下降，且下降超过5%时，模型停止训练，并将上一次训练好的模型作为最终模型。

3.7 初始模型不确定度分析

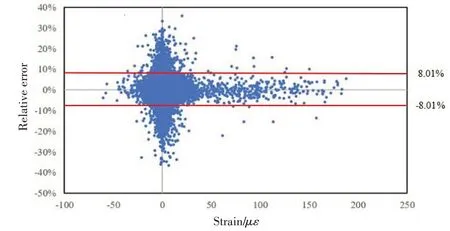
图15 S1方向全局应力求解不确定度Fig.15 Solving uncertainty for global stress in S1 direction

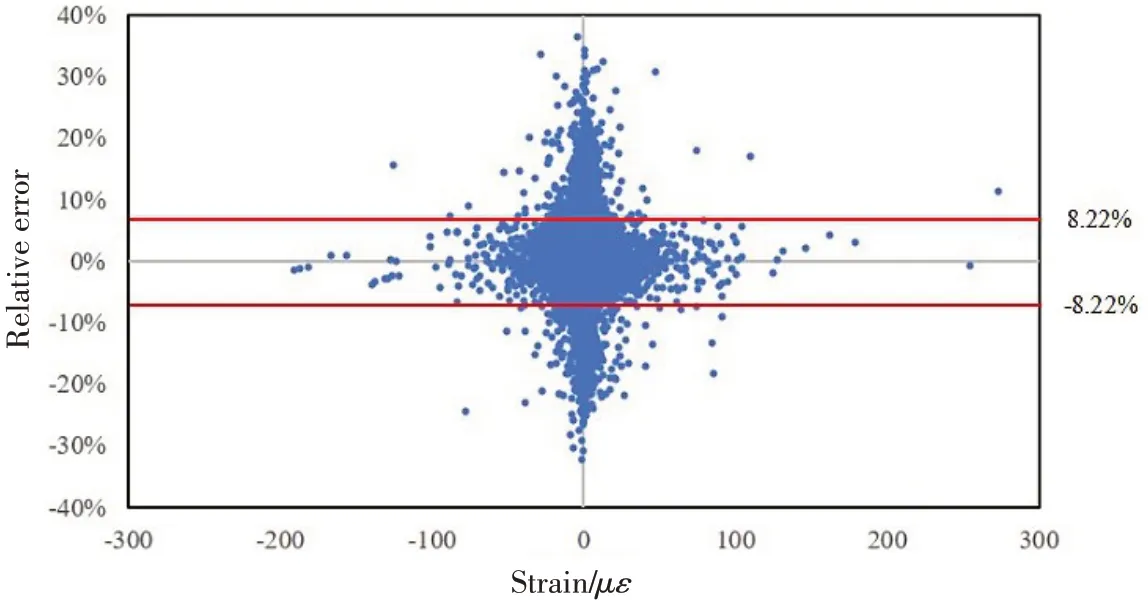
图16 S2方向全局应力求解不确定度Fig.16 Solving uncertainty for global stress in S2 direction

依托600 组测试集数据，对连接器结构应力场神经网络模型求解精度开展不确定度分析，图15～16为15 t剪力、300°剪切方向工况下由20个特征单元应力值作为输入，求解剩余的30 838个有限单元应力值与测试集数据的相对误差分布，横坐标表示应变值大小，纵坐标表示相对误差。在S1方向，95%的有限单元应力值求解误差在[-8.01%, 8.01%]区间；在S2方向，95%的有限单元应力值求解误差在[-8.22%,8.22%]区间。

4 连接器应力场人工智能模型修正与精度验证

4.1 连接器结构实尺度模型试验简述

取单耳连接器开展1:1 模型试验，验证神经网络模型对连接器结构应力场的求解精度，表2 为单耳连接器模型主要参数。

模拟平台约束条件（图17），采用加载工装块模拟双耳连接器，液压缸施加模拟剪切力。试验采用静态应变仪与应变片测试结构双向应力，通过力值传感器精确控制剪切力载荷，共设置27 个应力测点，其中20 个点用于建立AI 模型、5 个点用于修正、2 个点为任意位置的精度校验点。试验在弹性范围内进行，加载方案如表3所示，修正阶段与考核阶段试验载荷不重叠。

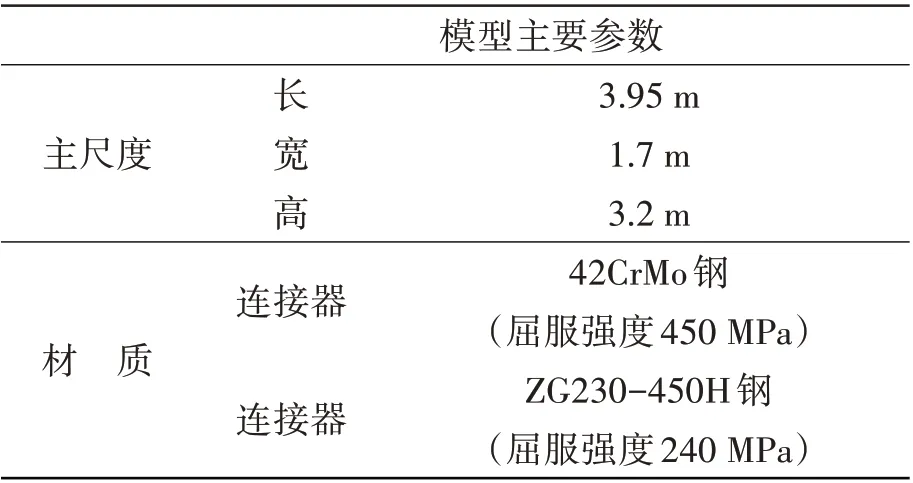
表2 连接器试验模型主要参数Tab.2 Main parameters of the connector model

图17 试验装配图Fig.17 Test assembly picture

表3 加载工况明细表Tab.3 Detailed loading conditions

4.2 精度考核结果

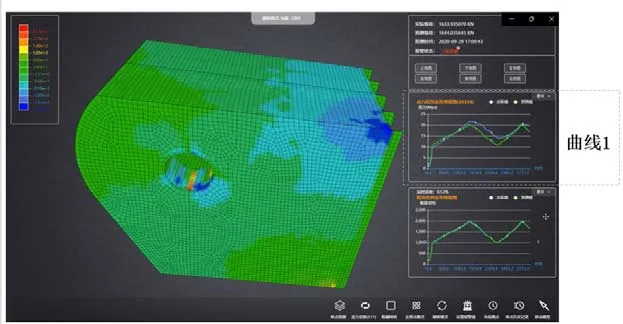
图18 1634 kN剪切力载荷下神经网络求解的结构应力云图Fig.18 Structural stress nephogram of digital twin system under shear load(1634 kN)

基于修正后的神经网络算法，编写连接器结构应力场实时求解软件，图18 为该软件在垂向剪切力（1634 kN）下求解出的应力场云图。图中，曲线1 为考核点实测应力值与神经网络求解出的应力值比对曲线，其中蓝色曲线为实测数据，绿色曲线为神经网络模型计算数据，通过比对得出求解精度高达93.6%；可识别载荷作用方向为垂直向上，最大应力位于连接器销轴孔下侧，同时销轴孔两侧与上侧均为高应力区，距离销轴孔越远的结构应力幅值越低，最大幅值约为20 MPa。