海洋平台垂荡作用下立管的非线性涡激振动特性研究
2023-03-01李凤明陈永訢
朱 磊,李凤明,陈永訢
(1.哈尔滨工程大学航天与建筑工程学院,哈尔滨 150001;2.海洋石油工程股份有限公司,天津 300461)
0 引 言
立管是连接海面平台与海底井口的重要通道,其涡激振动问题长期受到工程领域的关注。在一定来流作用下,立管两侧产生周期性的旋涡泻放,从而产生周期性的脉动压力,引发立管结构的剧烈振动,在复杂多变的海洋载荷作用下,立管表现出复杂的振动特性,尤其是与海洋平台相连接的立管,海洋平台的大幅垂荡与立管自身涡激振动相互耦合,对立管的安全生产造成了严重影响[1-2]。
在复杂的海洋环境条件下,海洋平台垂荡和立管涡激振动的耦合振动响应,表现出的振动形式更加复杂。这一问题,尤其是立管结构的稳定性,引起很多国内外学者的关注。Chatjigeorgiou 和Mavrakos[3-4]分别采用多尺度方法和数值方法分析了细长柔性结构的稳定性问题,并讨论了阻尼对稳定性的影响,结果表明,细长柔性结构失稳主要出现在一阶不稳定区,高阶失稳可能性较小,阻尼可以显著减小不稳定区的大小;Sinir[5]研究了微弯曲管道输送流体时的非线性振动,给出了不同振幅的曲率函数和流体速度的分岔图,在微弯曲管道输送流体的横向振动中,观察到了周期运动和混沌运动现象;Keber 和Wiercigroch[6]研究了结构非线性对二维输油管道涡激振动响应的影响,指出内部流体流动可以加强结构非线性对管道动力学响应的影响;Kuiper 等[7]采用Floquet 理论,分别讨论了参激振动稳定性问题和剧烈海况下立管底部出现负张力从而产生局部屈曲而导致的失稳问题。除稳定性问题之外,He 等[8]采用Galerkin 离散的方法研究了平台横向振动作用下立管的振动特性;唐友刚等[9]建立了柔性立管参激—涡激耦合振动的计算模型,计算了剪切流下立管振动响应特性;陈伟民等[10]考虑参激—涡激耦合效应,采用有限元方法离散立管模型,结果表明,立管振动响应幅值随振动模态阶数的降低而增大,同时出现模态转换现象。
可以看出,上述研究分别针对顶张力立管顺流向和横流向的非线性动力学响应,以及变张力作用下顶张力立管横流向涡激振动响应的影响进行研究。但是,将两者结合研究的文献很少,本文结合两方面的工作,将目前研究变张力对顶张力立管横流向涡激振动响应的影响拓展为二维问题,丰富了变张力对顶张力立管顺流向涡激振动响应的研究内容,且以往文献对于立管涡激振动响应的预报大多采用有限元法,本文将采用Hamilton 原理和Galerkin 方法建立结构运动方程,避免了采用有限元法的繁琐。
基于上述分析,本研究针对海洋平台垂荡运动,将其简化为轴向变化的顶张力,同时以Euler-Bernoulli 梁模型对立管结构进行建模,采用Hamilton 原理建立顶张力立管结构的二维非线性运动方程,并对运动方程进行无量纲化,采用Galerkin 方法对立管和涡尾迹的非线性方程进行离散,并用四阶Runge-Kutta方法进行求解,对可变顶张力立管的二维非线性涡激振动特性进行研究。通过与已有实验结果进行对比,验证本文方法和数值计算结果的可行性和正确性。
1 建立结构运动方程
1.1 结构模型
研究中的立管模型如图1所示。定义了一个笛卡尔坐标系,x轴为沿立管轴向,y轴为沿来流速度方向(IL 方向),z轴为垂直于来流速度方向(CF 方向)。该系统由一个两端铰接柔性立管组成,输送内部流体,柔性立管系统置于外部流体中。
采用Hamilton原理和Galerkin方法建立立管的非线性运动方程。Hamilton原理表示为

式中,Ttotal和Vtotal分别表示系统的总动能和总势能,WI为外力做的功,t为时间。
系统的总动能Ttotal包括空立管的动能T1和内部流体的动能T2,它们分别表示为

式中:mr为单位长度立管的质量;ma为单位长度附加流体质量,ma=CaπD2ρ0/4,D为立管的外径,ρ0为管外流体密度,Ca为附加流体质量系数,取Ca=1;mi为单位长度内部流体的质量;V和W分别为立管沿y轴和z轴的位移;L是立管的长度;Ui为管内流体流速。
系统的总势能Vtotal由立管的弯曲势能V1、重力势能V2和轴向拉伸势能V3构成,它们分别表示为
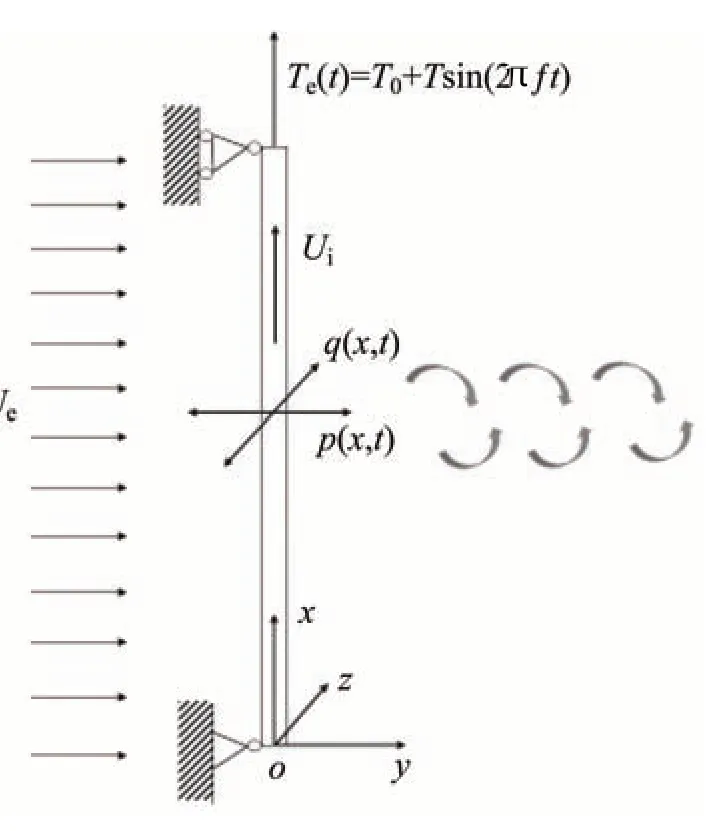
图1 立管示意图Fig.1 Schematic of riser

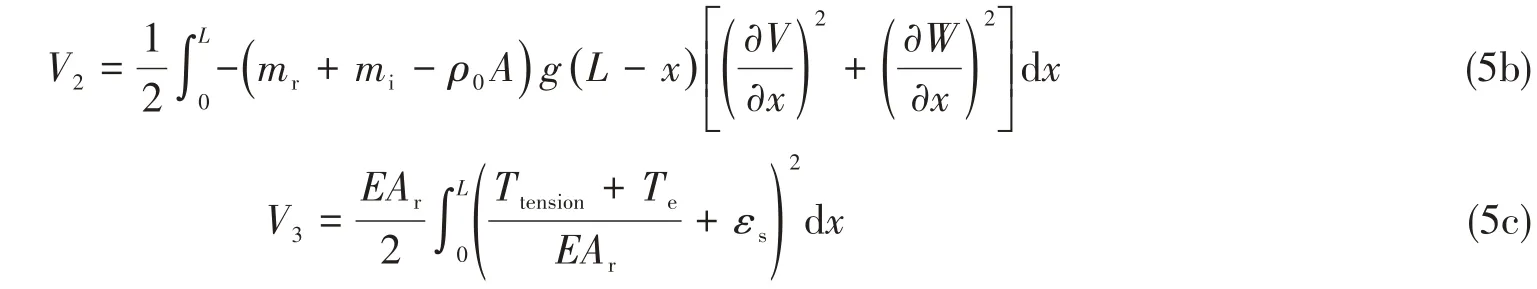
式中,EI和EAr分别为立管的弯曲刚度和拉伸刚度,A为立管排开水的截面面积,Ar为立管管材的截面面积,g为重力加速度,Ttension为轴向拉伸引起的非线性张力,Te为平台顶张力,εs为立管的应变。
由于本文研究的重点是立管的非线性动力学响应,因此需要考虑立管轴向应变引起的几何非线性。根据Jiang等[11]的工作,由轴向拉伸引起的非线性张力表示为
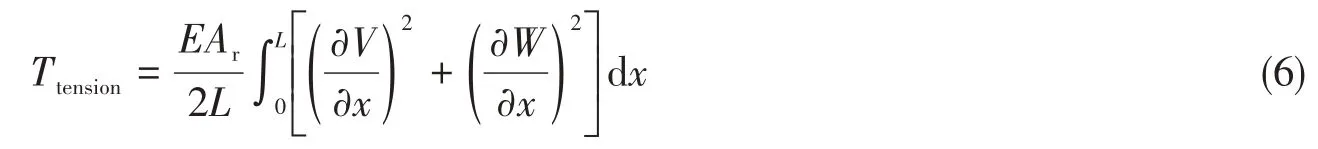
立管的应变εs表示为

式中,O(∈4)(∈<<1)为高阶小量。
外力做的虚功为

式中,cs为结构阻尼,cf为流体附加阻尼,Fy和Fz为管外流体作用在立管上的水动力。
将式(2)~(8)代入到式(1)中,利用变分原理,立管的IL 方向和CF 方向耦合的非线性偏微分运动方程可表示为[12]


式中,m为单位长度系统的总质量,m=mr+mi+ma。结构阻尼cs和流体附加阻尼cf可表示为[12]

式中:ζ为结构阻尼比,取ζ=0.05;ωr为立管振动的角频率;ϑ为水动力阻尼系数,根据Skop 等[13-14]的研究,取ϑ=0.8;ωs为旋涡脱落的角频率,可表示如下:

式中:Ue为来流速度;St为斯特劳哈尔数(Strouhal number),取St=0.2。
顶端海洋平台垂荡运动作用下立管顶张力可表示为[9]

式中,T0为预张力,T为可变张力幅值,ƒ为可变张力的频率(即海洋平台垂荡的频率)。
本模型的简支边界条件可表示为[15]

1.2 水动力和尾流振子模型
式(9)和式(10)中的Fy和Fz分别为IL 方向和CF 方向作用在立管上的水动力。对于固定圆柱结构,Fy和Fz分别与拖拽力fD和涡激升力fL相关,fD和fL的作用方向与IL和CF方向一致。然而,当立管在水动力作用下发生振荡时,拖拽力fD和涡激升力fL不再完全作用在y轴和z轴方向上。Fy和Fz可以表示为[16]

式中,fD可以看作是尾涡脱落的脉动拖拽力,fD0是作用在立管上的平均拖拽力,fL是作用在立管上的涡激升力。
此外,fD、fD0、fL可以分别进一步表示为[16]

式中,CDi是尾涡脱落的拖拽力系数,CD0是静止圆柱体的平均拖拽力系数,CL是升力系数。
立管漩涡脱落区尾流特性本文采用的是基于van der Pol方程的尾流振子模拟,该方法是一种半经验模式方法,不考虑具体的流场结构,而将流体和其中的振荡物体视为一个整体系统,把尾流看成是一个非线性振子,尾流振子的振动引起结构的振动,反过来,结构的振动又对尾流有一个反馈的作用。
根据Facchinetti等[16]和Srinil等[17-18]的研究,van der Pol尾流振子模型方程如下:

式中,εy、εz、Ay和Az是由实验得到的无因次参数,p(x,t)和q(x,t)分别表示IL和CF方向的尾流变量。
通过公式p(x,t)= 2CDi/CDi0和q(x,t)= 2CL/CL0,结构模型与尾流振子模型建立了联系,且Fy和Fz整理后可以进一步表示为
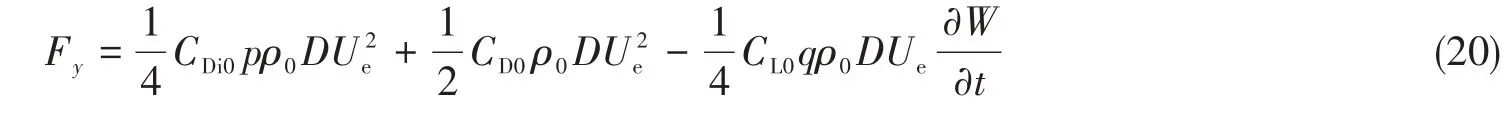

式中,根据文献[17],取CDi0=0.1,CD0=2.0,CL0=0.3。
Wang等[12]的研究中,讨论了三维柔性管振动中参数的选取,当四个无量纲参数设置为εy=0.02,εz=0.04,Ay=96和Az=12时,理论结果与实验数据吻合较好。需要注意,van der Pol尾流振子模型是半经验半解析的,该经验模型忽略了涡型和涡强等细节。然而,用van der Pol 模型预测的立管涡激振动响应与直接数值模拟预测的结果吻合较好。
1.3 Galerkin离散化
借助于下列无因次量:

式(9)、式(10)、式(19)、式(20)的耦合方程可以写成以下无量纲形式:

为了离散立管和尾流的无量纲运动方程,采用以下Galerkin离散化方案[19]:

式中,φi(ξ)= 2 sin( )iπξ是简支梁的本征函数(τ)、(τ)、(τ)、(τ)是相应的广义坐标。
为了保证结果的收敛性,在接下来的分析中,截取前六阶模态N=6。将式(27)~(28)代入式(23)~(26),等式两边乘以φi(ξ),从0到1积分,然后利用模态的正交性,可以将偏微分方程转化为一组常微分方程:


利用四阶Runge-Kutta法可以进一步数值求解离散化的常微分方程,得到结构的位移响应等物理量。
2 模型验证
埃克森美孚公司Lehn[20]在挪威海洋工程研究中心测试了垂直立管模型在均匀流和剪切流中的涡激振动响应。Wang 和Xiao[21]利用CFD 方法模拟了立管在均匀流作用下的涡激振动响应。立管的主要参数:立管长度为9.63 m,外径为20 mm,壁厚为0.45 mm,质量比为2.23,长细比为481.5,顶张力为817 N,弹性模量E=1.025×1011N/m2,抗弯刚度EI=135 N·m2。不考虑结构阻尼,立管垂直安装,两端铰接。
针对不同的来流速度,IL 和CF 方向的涡激振动运动轨迹沿立管长度的分布分别如图2~3 所示。当Ue=0.2 m/s 时,计算结果如图2 所示:对于IL 方向,用本理论模型预测的运动轨迹表明,振动以第二阶模态为主,这与实验数据和CFD 仿真结果一致,且IL 方向振幅的数值计算结果也是可以接受的;对于CF方向,用本理论模型预测的运动轨迹表明,振动以第一阶模态为主,这与实验数据和CFD仿真结果一致,且CF 方向振幅的数值计算结果也是可以接受的。当Ue=0.42 m/s时,计算结果如图3所示,对于IL 方向,用本理论模型预测的运动轨迹表明,振动以第三阶模态为主,这与实验数据和CFD 仿真结果一致;对于CF 方向,用本理论模型预测的运动轨迹表明,振动以第二阶模态为主,这与实验数据和CFD 仿真结果一致。由于本文考虑了立管非线性效应的影响,致使采用本文方法计算的立管响应包络图幅值小于文献[20-21]中的实验和CFD仿真计算结果。

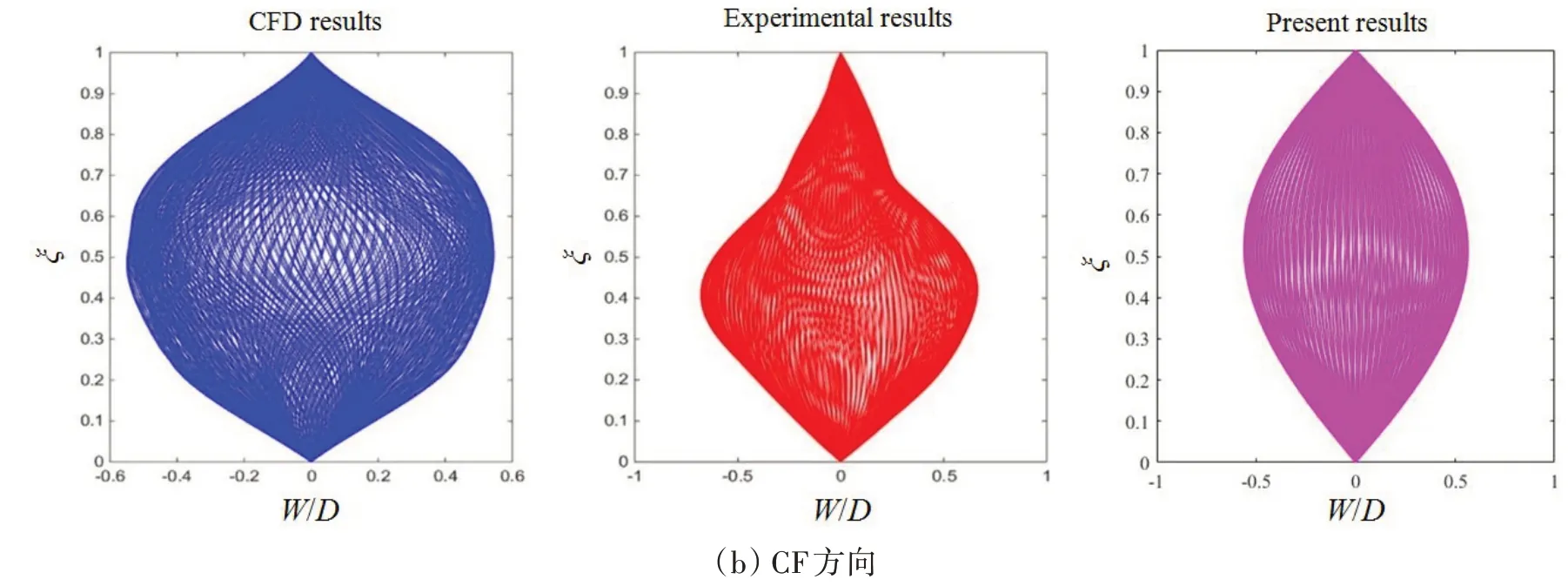
图2 立管运动轨迹的比较(Ue=0.2 m/s)Fig.2 Comparison of the riser’s response envelopes for Ue=0.2 m/s

图3 立管运动轨迹的比较(Ue=0.42 m/s)Fig.3 Comparison of the riser’s response envelopes for Ue=0.42 m/s
3 顶张力对立管涡激振动的影响
本章计算采用的立管模型及工况主要参数如表1所示。

表1 立管模型的参数Tab.1 Parameters of the riser model
3.1 顶张力对立管固有频率的影响
在研究有支撑的管道输送流体的动力学过程中,可以很容易地用线性理论预测最低的几阶固有频率。根据线性理论,将式(22)和式(23)中的非线性项、外流激励项和重力项去掉,整理后得到
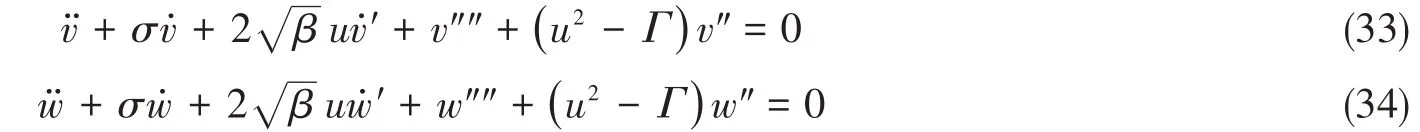
图4 为Ui=0,T0=0~460.42 kN,T=0 时,顶张力在该区间变化时对立管固有频率的影响。选取立管前四阶固有频率进行研究,结果表明:相同阶次下的立管固有频率随顶张力增加逐渐增大,并且随着立管固有频率阶次增加,立管的固有频率随顶张力的变化越快。立管固有频率随顶张力的变化规律可以很好地解释下文的模态转换现象。
3.2 顶张力作用下的立管涡激振动模态转换
为了考察平台运动对立管涡激振动的影响,取两种计算状态:(1)立管上只作用涡升力,海洋平台固定不动;(2)立管上作用涡升力,同时海洋平台沿轴向(x轴)做简谐运动。
立管在水中的湿重为(mr+mi-ρ0A)gL=160.42 kN,文中Te(t)为立管顶部的张力,为了保证立管底部不出现负张力,必须满足Te(t)=T0+Tsin(2πft)≥160.42 kN。第一种计算状态:不考虑平台运动,即T=0,为了满足Te(t)=T0+Tsin(2πft)≥160.42 kN,取T0=160.42 kN。第二种计算状态:可变张力部分取T=150 kN,为了满足Te(t)=T0+Tsin(2πft)≥160.42 kN,取T0=310.42 kN。
图5 给出了当预张力T0=160.42 kN,变张力幅值T=0,外部流体流速Ue=0.2 m/s 时,立管的位移响应。从图5(c)中可以看出,立管IL 方向的位移响应对应第三阶模态,从图5(d)中可以看出立管CF 方向的位移响应对应第二阶模态。

图4 顶张力对立管固有频率的影响Fig.4 Effect of top tension on the natural frequency of the riser


图5 立管的位移响应(T0=160.42 kN)Fig.5 Displacement response of the riser(T0=160.42 kN)
图6 给出了当预张力T0=460.42 kN,变张力幅值T=0,外部流体流速Ue=0.2 m/s 时,立管的位移响应。从图6(c)中可以看出立管IL方向的位移响应对应第二阶模态,从图6(d)可以看出立管CF方向的位移响应对应第一阶模态。通过对比可以发现,不同顶张力作用下立管的涡激振动模态发生了变化。
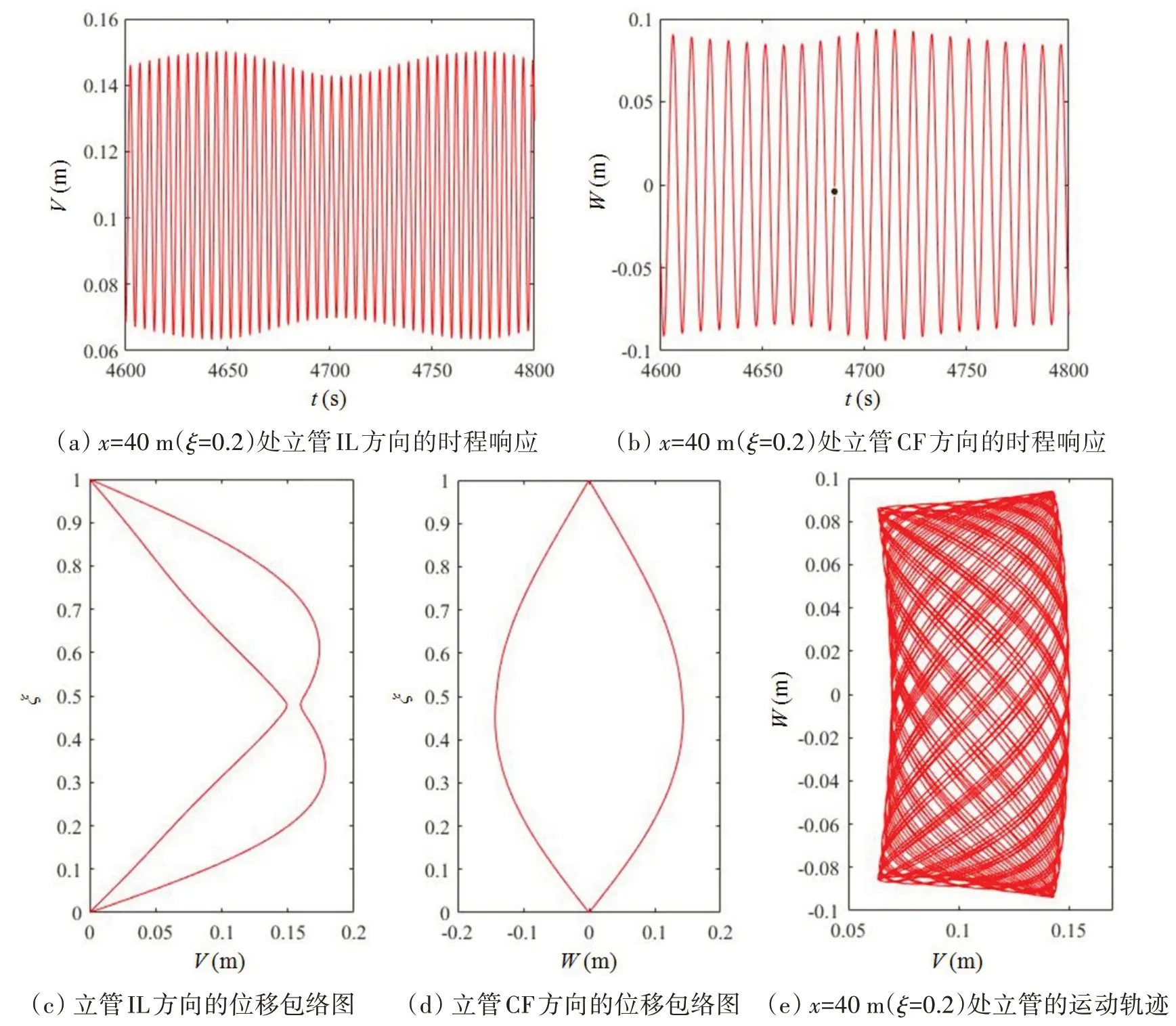
图6 立管的位移响应(T0=460.42 kN)Fig.6 Displacement response of the riser(T0=460.42 kN)
时变顶张力作用下立管的耦合位移响应见图7,此时,外部流体流速Ue=0.2 m/s,预张力T0=310.42 kN,变张力幅值T=150 kN,平台垂荡频率f=0.002 Hz。从图7(a)可见,t=4850 s附近立管IL方向的位移响应V=0.3368~0.4122 m,此刻IL 方向的耦合位移响应与图5 相比基本相同;t=4850~5122 s,立管IL 方向的位移响应先减小后增大(V=Vmax-(Vmax+Vmin)/2);t=5122 s 附近立管IL 方向的耦合位移响应V=0.0873~0.1283 m,此刻IL 方向的耦合位移响应与图6 相比略有减小。从图7(b)可以看出,t=4850 s 附近立管CF 方向的耦合位移响应W=-0.172~0.1722 m,此刻CF 方向的耦合位移响应与图5 相比基本相同;t=4850~5122 s,立管CF方向的耦合位移响应先减小后增大;t=5122 s附近立管CF方向的耦合位移响应W=-0.0893~0.0893 m,此刻CF方向的耦合位移响应与图6相比基本相同。经上述对比发现,立管IL方向的耦合位移响应在第二模态和第三模态之间周期性交替出现,立管CF方向的耦合位移响应在第一模态和第二模态之间周期性交替出现,且随着张力的变化,立管的耦合位移响应幅值周期性地先减小后增大。这种现象的发生,主要是由于立管轴向张力的变化,使得立管固有频率随之变化,从而导致立管发生耦合位移响应的主要模态交替出现。
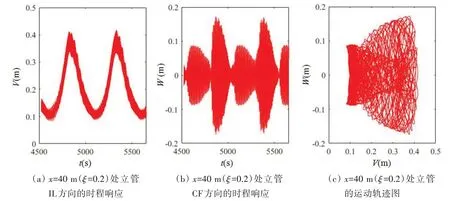
图7 立管的耦合位移响应(f=0.002 Hz)Fig.7 Coupled-displacement responses of the riser(f=0.002 Hz)
与图7相同工况下,仅将平台垂荡频率变为f=0.008 Hz,立管的耦合位移响应见图8。经对比可以发现,平台垂荡频率对立管IL 方向的耦合位移响应影响较小,但对立管CF 方向的耦合位移响应影响较大。这可能是由于高频激励作用下张力变化较快,所产生的影响尚未充分发展,张力就已经改变,因此没有产生较大的耦合振动响应。
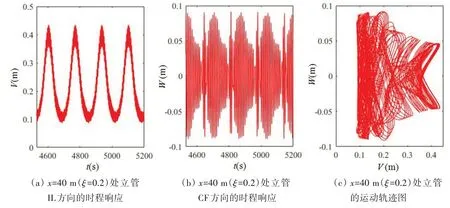
图8 立管的耦合位移响应(f=0.008 Hz)Fig.8 Coupled-displacement responses of the riser(f=0.008 Hz)
4 结 论
本研究考虑了内部流体作用下平台顶张力对立管非线性动力学特性的影响,研究了平台垂荡和立管涡激振动的耦合振动响应,并与立管单独涡激振动结果进行了比较。通过与已有实验数据进行对比,验证了本文分析方法的合理性。本研究得到了如下结论:
(1)在考虑海洋平台垂荡和立管自身涡激振动的耦合振动响应时,由于海洋平台的剧烈运动导致顶张力大幅度周期性变化,从而改变了立管的固有频率,在一定来流速度下,引发立管产生不同模态的涡激振动。
(2)随着顶张力的变化,立管的耦合响应在相邻模态间转化,立管的耦合位移响应幅值周期性地先减小后增大,且随着平台垂荡频率的增加,立管CF方向的耦合位移响应反而减小。
