基于GC-IMS的白酒特征分析及鉴别

鲁祥凯，杨 彪*，孙 莹，贺金娜，樊保民，孙 辉，孙啸涛

（1 北京工商大学化学与材料工程学院 北京 100048 2 江苏今世缘酒业股份有限公司 江苏淮安 223411 3 山东海能科学仪器有限公司 山东德州 253000 4 北京工商大学轻工科学技术学院 北京 100048）

白酒中丰富的微量组分及独特的风味，来源于酿酒原料的差异以及发酵过程中微生物群落的多样性和特异性[1]。白酒的人工品评鉴别是基于对组分的非定性、非量化的感官判断，判别标准因人而异[2-3]。 白酒的仪器鉴别主要通过来自原料和发酵产物的差异性特征组分信息来进行判别。 自1964年初次采用层析法定性白酒中的一些微量成分以来，已发展出光谱、色谱结合质谱以及传感器等仪器分析方法，结合模式识别可对白酒的香型、等级、年份以及产地进行鉴别[4-10]。

根据微量无机元素或同位素含量等反映酿酒原料特征的信息可较为准确地鉴别白酒[11-14]。姜涛等[15]检测黔、川两地白酒中15 个特征元素，根据其中6 种元素（Mn、Ga、Sc、V、Na 和Cs）含量建立了两种判别模型，对两地白酒的产地鉴别正确率分别为94.7%和100%。 李清亮等[11]依据12 种无机元素聚类分析结果，成功将12 个品牌共175 份白酒样品的分为4 类。 然而，生产批次、储存时间以及粮源变化会导致信息的不稳定，因此该类方法仅作参考。

通过对白酒中某些组分的定性、 定量分析或者采集特定范围内的光谱也可鉴别白酒[16-21]。霍丹群等[22]采用气相色谱分析技术，定性、定量分析7种不同产地白酒中的10 种组分，通过主成分分析建立的判别模型对未知酒样鉴别正确率为93.9%。 徐睿等[23]通过多种处理方法对8 种白酒（金沙蓝钻酒和其它白酒） 的近红外光谱进行处理，最终以4 119.20～9 881.46 cm-1区间的光谱特征建立金沙蓝钻酒相似度匹配模型，鉴别正确率达100%。白酒中某些物质与传感器的特异性响应也可用于白酒的鉴别[24-28]。Li 等[29]使用电子鼻结合多维尺度支持向量机算法实现对10 个品牌白酒98.3%的正确鉴别。 田婷等[30]采用电子鼻结合主成分分析实现对酱香型白酒分类识别。然而，传感器主要是针对白酒中特定物质种类进行响应，无法做到全方位分析，有时还受到酒精的影响[10]。 上述常用的白酒仪器鉴别方法沿袭了白酒风味分析的原理，需对白酒中确定的风味组分进行定性、定量或半定量检测分析，进而提取特征建立鉴别模型，存在局限性。目前，尚未建立类似人工品评的仪器方法，可以在未定性具体组分情况下，仅依据组分宏观差异来鉴别白酒。

近年来，气相色谱-离子迁移谱法（GC-IMS）凭借高分离效率、 高灵敏度以及响应速度快的优势逐渐成为检测分析挥发性有机物的有效方法[31-33]。GC-IMS 检测获取的风味特征指纹图谱，不仅能可视化分析微量组分差异，还能提取主要特征并建立鉴别模型。 Chen 等[34]依据指纹图谱区分3 个产地共122 个黄酒样品，建立二次判别模型，对训练集产地分类正确率为97.47%，预测集正确率为95.35%。 Zhou 等[35]从不同年份的白云边陈酿酒的特征风味指纹图谱中选取60 个特征，结合主成分分析可将3年和5年陈酿完全区分，而15年和20年陈酿因过于相似而无法完全区分。

本文将2 种香型（含2 种酒精度）的10 种白酒直接顶空制样进行GC-IMS 分析，获得指纹图谱，在未定性、定量前提下，通过指纹图谱中各微量组分相对含量提取白酒特征，建立Fisher 线性判别模型，以实现对不同香型、酒精度以及不同档次白酒的准确鉴别。

1 材料与方法

1.1 材料与主要仪器

白酒样品取自江苏某酒企。 选取42 度和52度共10 种不同档次和香型的白酒，为确保样品的代表性，每种白酒分别取2 个不同勾调批次的样品。 白酒样品采用A-B-C 代码表示，其中A 代表酒精度，B 代表酒样序号，C 代表勾调批次。 如：42-1-2 表示42 度白酒1 号第2 个勾调批次样品。42 度白酒的1～5 号样品为浓香型，6 号为清雅酱香型；52 度白酒中1～3 号样品为浓香型，4 号为清雅酱香型。

气相色谱-离子迁移谱仪（FlavourSpec 1 H1-100053），德国GAS 公司，配套美国Restek 公司Rtx-Wax 色谱柱（30 m×0.53 mm，1 μm）以及瑞士CTC 公司自动顶空进样装置（Combi PAL）。

1.2 测试方法

样品于室温下密封避光储存。 测试时采用顶空制样并对制样条件进行优化。 优化后的顶空制样条件为：取原始白酒样品0.5 mL 置于20 mL 顶空瓶中密封，70 ℃加热振荡孵化15 min，由顶空瓶上部空间取样200 μL 用于检测，顶空进样针温度为85 ℃。

设定GC-IMS 测试条件：气相色谱柱温度60℃，漂移管温度45 ℃。 气相色谱载气流速：0～2 min：2 mL/min；2～10 min：2～10 mL/min；10～30 min：10～90 mL/min；30～40 min：90 mL/min。 离子迁移谱漂移气恒定流速150 mL/min。 载气和漂移气均为氮气（纯度99.999%）。 每个白酒样品重复测3次。

2 结果与分析

2.1 白酒挥发组分分析

从白酒样品中共检测到水和乙醇之外的134种挥发组分（含二聚体），见表1。 由已有数据库可定性其中65 种物质，其余69 种为未定物。

表1 白酒中检测到的挥发组分Table 1 Volatile substances in Baijiu

（续表1）

（续表1）

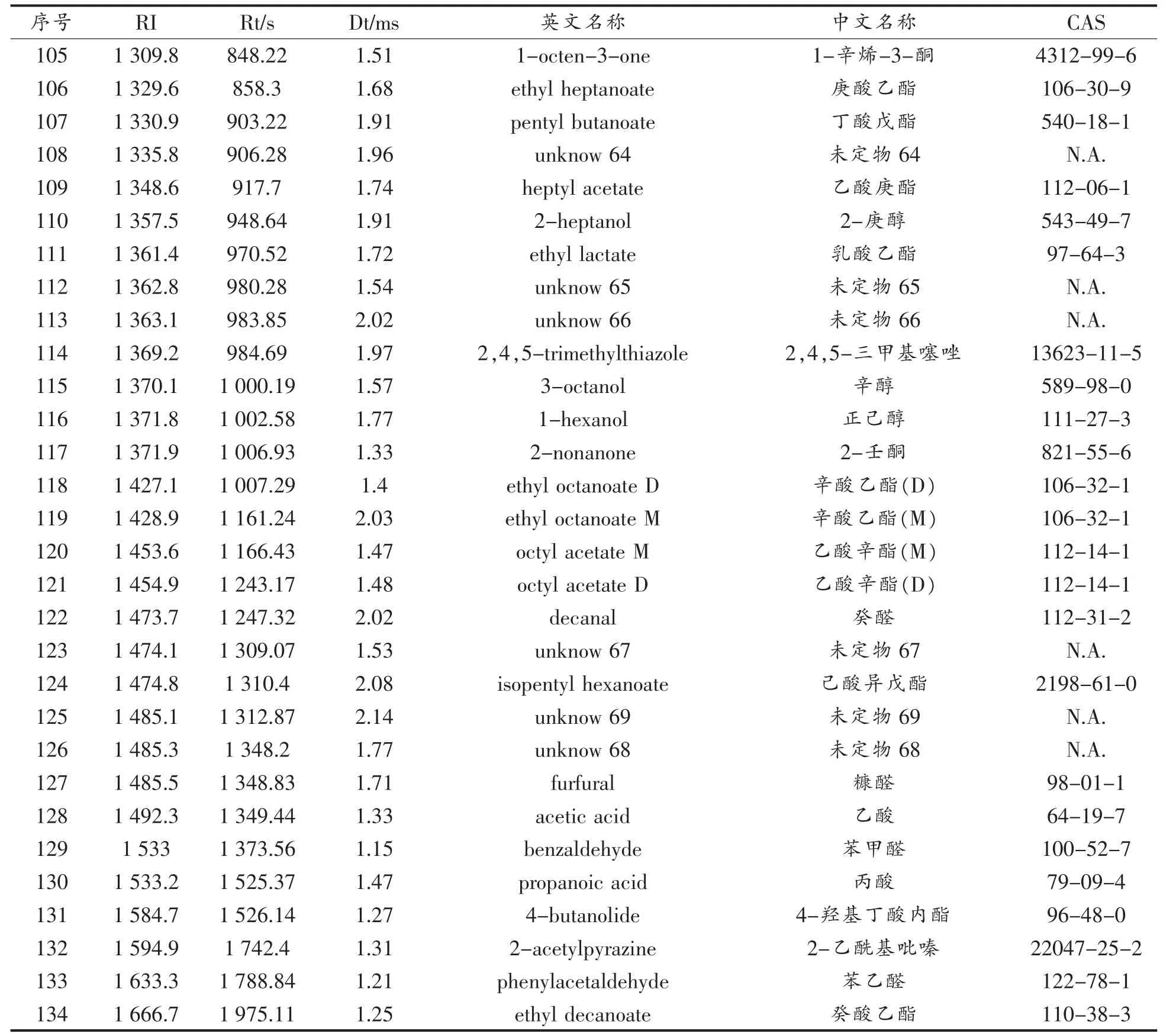
（续表1）

将所有挥发性组分信号峰提取后形成指纹图谱（图1）。 其中，每个点代表一种物质，颜色越红表示物质浓度越高。 横轴为样品中检测到的所有挥发组分，纵轴为同一挥发组分在不同白酒样品中的浓度差异。由图1 可以发现，虽然酒精度和香型不同，但是指纹图谱中部蓝色区域内的组分为白酒的共有特征组分。 清雅酱香型白酒42-6 和52-4 的图谱类似，且与其它香型白酒图谱差异明显。指纹图谱左侧黄色区域内的大部分组分，在清雅酱香型白酒中的浓度要明显低于浓香型白酒，而谱图中绿色及右侧黄色区域中2-甲基丁酸乙酯、乙酸叶醇酯、乙酸异戊酯、2-己醇、糠醛等组分在清雅酱香型白酒中的浓度则明显高于浓香型白酒。这反映出白酒香型不同导致的组分差异。作为低端产品的42-2 和52-1 浓香型白酒，在图谱两侧黄色区域中的组分浓度明显低于其它浓香型白酒。另外，每种白酒平行测试3 次的结果无明显差异，说明GC-IMS 法的稳定性很好。 除42-3 和52-1 两种白酒的批次之间有较明显差异外，其它白酒的批次差异不明显，说明其勾调批次稳定性较好。以上简单分析可知，指纹图谱能够清晰直观地反映白酒样品中微量挥发组分的含量差异以及白酒勾调批次的稳定性。

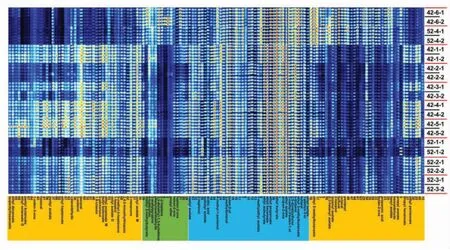
图1 白酒样品挥发物质指纹图谱Fig.1 Fingerprints of volatile substances in Baijiu samples

根据GC-IMS 测试数据计算得到10 种白酒样品的平均欧氏距离（表2）。 欧氏距离越大，两样品间差异越大，反之则相似度越高。结合指纹图谱分析可知，每个样品平行检测3 次的结果十分稳定，欧氏距离均小于0.65（表2 中粗体数据）。同一样品批次之间的差异（表2 中灰色阴影数据），除样品42-3 和样品52-1 的批次差异较明显（欧式距离分别为1.680 和1.554）外，其它样品批次差异均小于1。 因此，欧氏距离也可直观反映白酒生产过程中的勾调稳定性。 由表2 数据可知，样品42-1、42-3、42-4 和42-5 较为相似，42-2 与52-2较为相似，52-2 与52-3 较为相似，42-6 与52-4较为相似，与可视化的指纹图谱结论一致。 综上，采用GC-IMS 检测白酒中挥发组分，不仅结果稳定性好，还能反映不同批次间的质量稳定性，可直接应用于白酒生产过程中的质量监控。

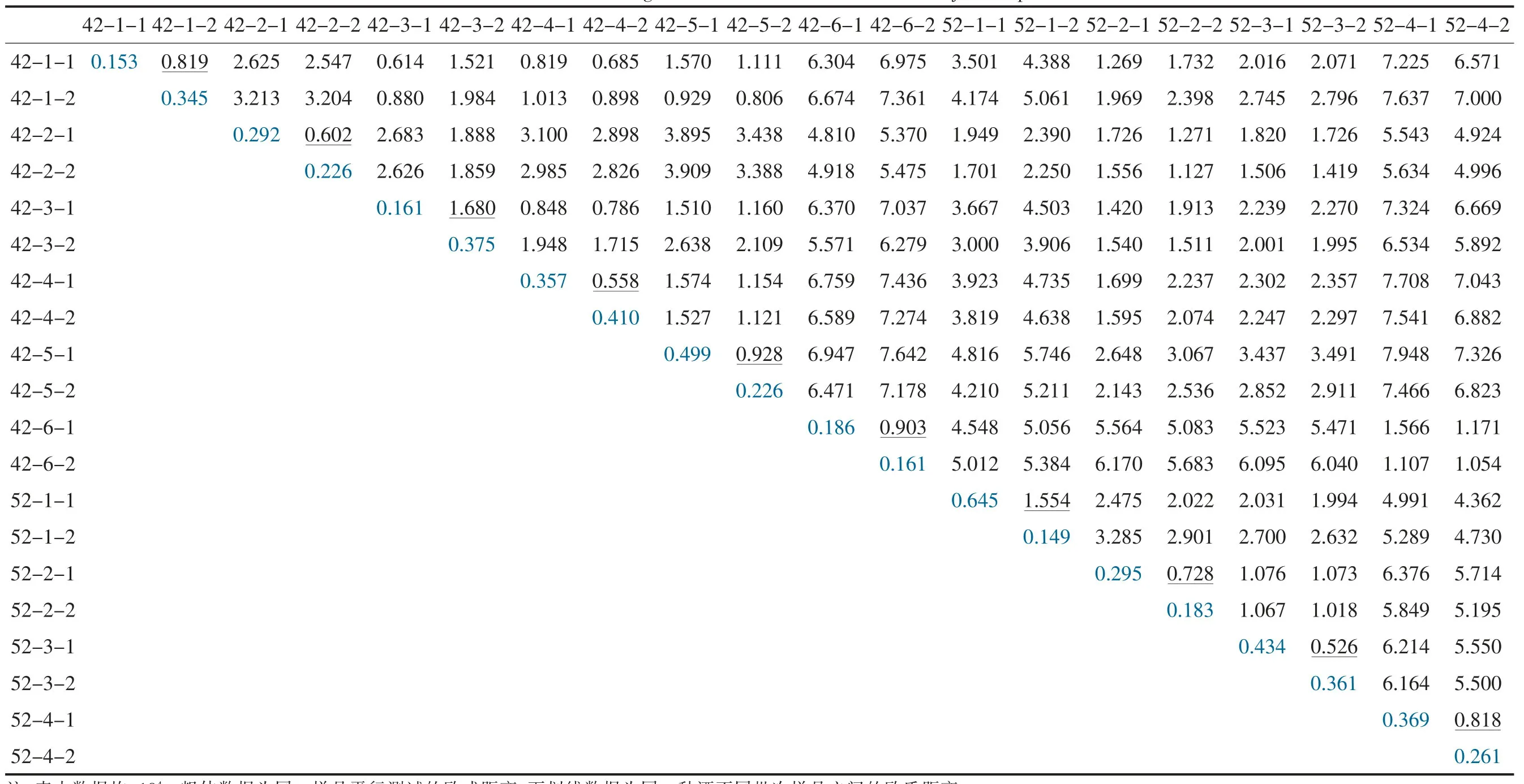
表2 白酒样品间平均欧氏距离Table 2 The average Euclidean distance between Baijiu samples

2.2 白酒鉴别模型

建立白酒的鉴别模型前，首先需要获取白酒的主要特征，常用的方法有特征选择和特征提取两种。两种方法均是对原有特征的降维处理，区别在于是否改变特征的属性。 特征选择从原始特征中筛选子集，未改变其属性。主要是从准确性和特征维数考虑，根据相关程度或其它角度从原始数据中筛选，形成具有较高正确率的特征子集[36-37]。特征提取则是对原始特征进行数学变换，通过线性组合（如主成分分析）形成相互独立的新特征，有效地解决“维数灾难”[38]。

本文基于顶空制样所测得的60 组数据，在兼顾样品品质和香型的前提下随机取样，消除类别属性，从中划分出20 个独立样本，作为测试集，剩余样本作为训练集。 分别依据相关性分析和主成分分析对训练集数据进行主要特征提取，然后建立Fisher 线性判别模型并进行交叉验证，最后对测试集样品进行判别验证。

2.2.1 特征选择（相关性分析） 显而易见，浓度差异显著的组分对白酒的鉴别意义更大。 需要通过相关性分析，对原始数据进行特征筛选，获得白酒的鉴别特征。 本文对所有组分特征进行皮尔逊双尾相关性检测，保留与组变量相关性系数α≥0.4 且显著相关（P＜0.05）的变量，筛除相关性弱以及相对冗余的变量，最终提取出39 个特征组分变量。 相关性分析部分见表3。 由表3 可知，白酒类别相关性较大的39 个组分变量在0.01 水平相关性显著，具有统计学意义。 其中有20 个组分为正相关变量，依据相关性排序为未定物49（0.752）、未定物59（0.629）、未定物3（0.609）、2-乙酰基吡嗪（0.608）、未定物10（0.553）、未定物8（0.535）、乙酸叶醇酯（0.533）、未定物7（0.523）、未定物9（0.482）、乳酸乙酯（0.469）、丙酸（0.464）、未定物58（0.464）、未定物12（0.447）、2-己醇（0.446）、未定物5（0.437）、2，3-二甲基-1，3-丁二烯（0.430）、3-甲基-3-丁烯-1-醇（0.427）、乙酸异戊酯（0.411）、未定物4（0.409）、正戊醇（0.407）；另外19 个组分为负相关变量，依据相关性排序为乙酸辛酯（M）（0.754）、未定物53（0.690）、异丁酸乙酯（0.606）、辛酸乙酯（M）（0.583）、癸酸乙酯（0.583）、未定物19 （0.569）、2，4，5-三甲基噻唑（0.553）、未定物60（0.545）、50（0.490）、26（0.477）、36（0.472）、31（0.462）、65（0.445）、5-甲基-3-庚酮（0.439）、未定物69（0.428）、68（0.425）、33（0.420）、丁酸戊酯（0.417）、未定物64（0.414）。通过相关性分析可知，白酒样品间的差异主要来源于更微量的组分（非主体风味物质），而不是相对含量更高的物质（主体风味物质）。

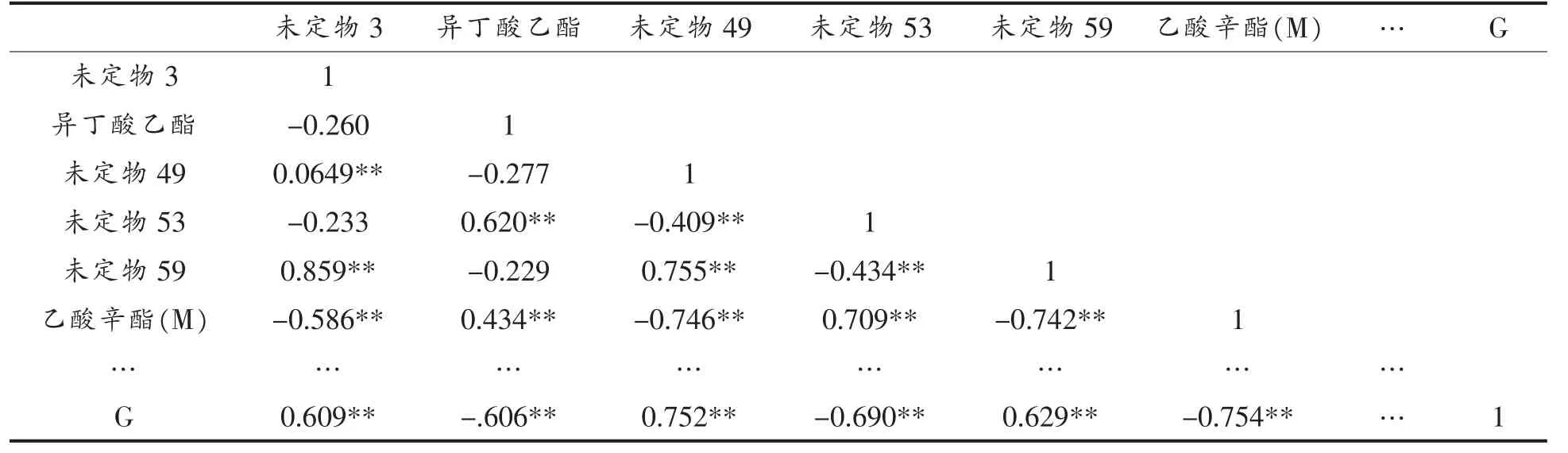
表3 白酒特征相关性分析（部分）Table 3 Correlation analysis of Baijiu characteristics （part）

2.2.2 特征提取（主成分分析） 主成分分析可将原始特征变换成新的特征向量，且能够保证相互之间正交。为分析各特征对白酒组分的贡献，本文采用最大正交旋转变换，使每个变量中解释的因子量最少。以特征值大于1 为阈值，共选取6 个主成分，相关矩阵特征值见表4。 6 个主成分可以反映原特征信息的92.648%，基本保留了原始特征，具有合理性。

表4 相关矩阵特征值Table 4 Eigen values of the correlation matrix

以表1 中各物质顺序依次分别记作变量X1、X2、X3……X134，通过主成分分析获得原始变量与各主成分之间的相关程度，见表5。 通过主成分分析获得6 个相互独立的综合指标模型：

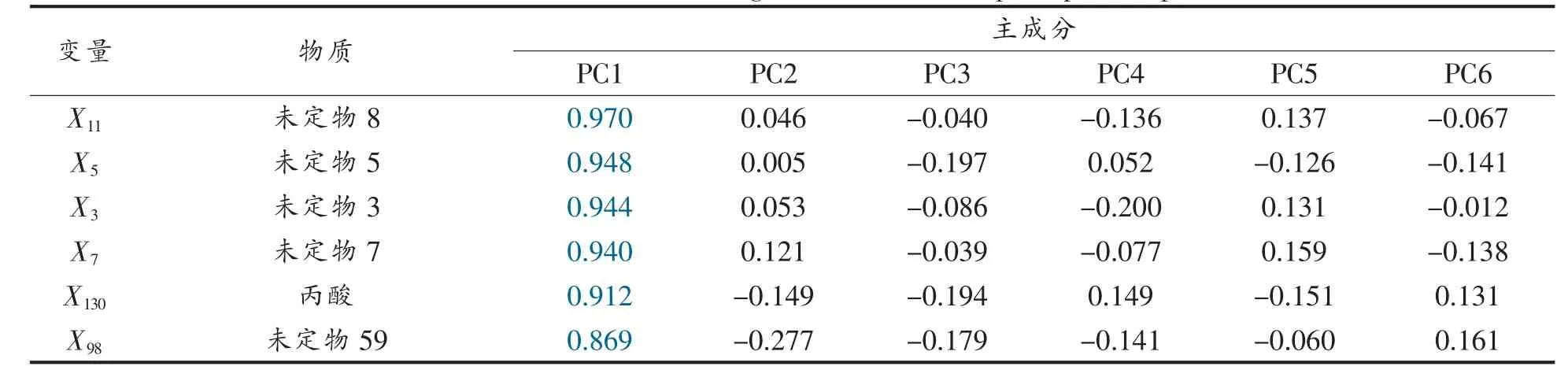
表5 原始变量与各主成分之间相关程度Table 5 Correlation between original variables and principal components

PC1 = 0.970 X11+ 0.948 X5+ 0.944 X3+……-0.376 X114，可反映原数据标准变异的53.530%，代表变量为未定物8、丙酸、正戊醇等；

PC2=0.046 X11+……+0.961 X107+0.951 X112+……+ 0.372 X114，可反映原数据标准变异的19.987%，代表变量为丁酸戊酯、未定物65、癸酸乙酯等；

PC3 = - 0.040 X11+……+ 0.910 X88+ 0.846X108+……+0.448 X114，可反映原数据标准变异的7.136%，代表变量为5-甲基-3-庚酮、未定物64、未定物33 等；

PC4=-0.136 X11+……+0.920 X29+0.654 X47+……-0.376 X114，可反映原数据标准变异的6.000%，代表变量为异丁酸乙酯、未定物26 等；

PC5 = 0.137 X11- 0.126 X5+ 0.131 X3+……+0.058 X114，可反映原数据标准变异的3.397%；

PC6=-0.067 X11-0.141 X5-0.012 X3+……+0.518 X114，可反映原数据标准变异的2.598%。

（续表5）

计算各主成分得分，以PC1、PC2 和PC3 为坐标轴，绘制主成分三维得分图（图2），可以对白酒进行分类。 42-6 和52-4 为清雅酱香型白酒，聚类区域与其它浓香型白酒相距较远，且这两种酒之间区分较为明显。 浓香型白酒相距较近，除了42-3 和52-1 批次差异较大，导致同类酒样本分散外，其它酒聚类范围均较小，然而，也发现42-1 和42-5 相距十分近。 由此可知，基于主成分分析的分类方法能够反映白酒风味的相似性与典型性。

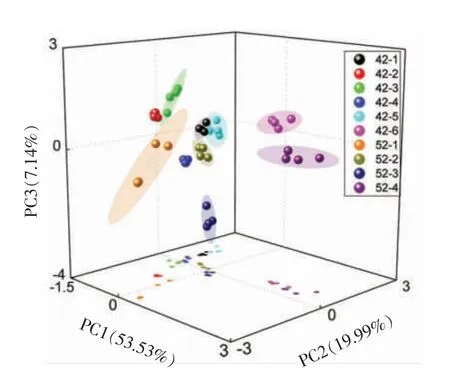
图2 白酒样品主成分三维得分图Fig.2 Three-dimensional score map of principal components in Baijiu samples

2.2.3 Fisher 线性判别模型 Fisher 线性判别是典则判别中常用的一种方法，主要是将高维空间内样本坐标投影至低维空间内进行分类，投影原则是同类差异最小化，异类差异最大化，分类完成后获得每类的组质心坐标，对未知样本进行鉴别时同样采用就近原则进行判别[39]。 本文分别将全部134 个组分特征数据，根据相关性筛选出的39个组分特征数据以及特征提取的6 个主成分作为Fisher 线性判别分析的数据集，分别建立白酒的Fisher 线性判别模型。 这3 个模型对训练样本的分类正确率均为100%，而交叉验证分类正确率依次为17.5%，67.5%和90%。 说明对原始数据进行特征提取，可有效提高模型鉴别正确率，然而同时也发现模型缺乏优化，效果较差。本文结合逐步回归分析对判别模型引入的特征进一步优化。 其基本思路是将变量依次选入，当其对因变量影响显著时保留，不显著则移除，继续引入新的变量，若被移除的变量在新变量引入后变得重要时，则重新被引入[40]。 通过不断拟合，直至达到鉴别效果最优的模型。 本文中条件设置为：F 概率P 值选入和移除阈值分别为0.05 和0.1。

将全部134 个特征数据采用逐步回归分析拟合26 次，获得最优模型，记作M1。 M1 采用24 个主要组分特征，分别为未定物8、9、17、20、22、29、31、47、51、53、56、59、65，乙酸乙酯、2，5-二甲基呋喃、丙酸乙酯、2-甲基丁酸甲酯、2-己酮、异戊醇、乙酸戊脂、正辛醛、乳酸乙酯、正己醇和2-壬酮。Wilk's Lambda 检验结果P=0.000，说明该模型具有统计学意义。取9 个判别函数，其特征值分别为207474.591，7530.331，1512.763，374.611，337.366，49.578，45.563，34.382 和7.277，分别能够解释模型方差变化的95.449%，3.464%，0.696%，0.172%，0.155%，0.023%，0.021%，0.016%和0.003%。 前2个Fisher 线性判别函数总共可解释98.913%的方差变化，包含了主要的信息，可描述各特征的差异与联系。 以前2 个Fisher 线性判别函数作散点图（图3）。 图3 中10 种白酒彼此分隔，同种白酒聚敛程度十分好，基本以组质心为中心聚拢，且测试集的白酒样品基本分布于各组质心附近。 该模型对训练集鉴别正确率达100%，采用留一法交叉验证正确率也为100%。所建立模型的Fisher 线性判别函数的系数见表6，各组质心见表7。

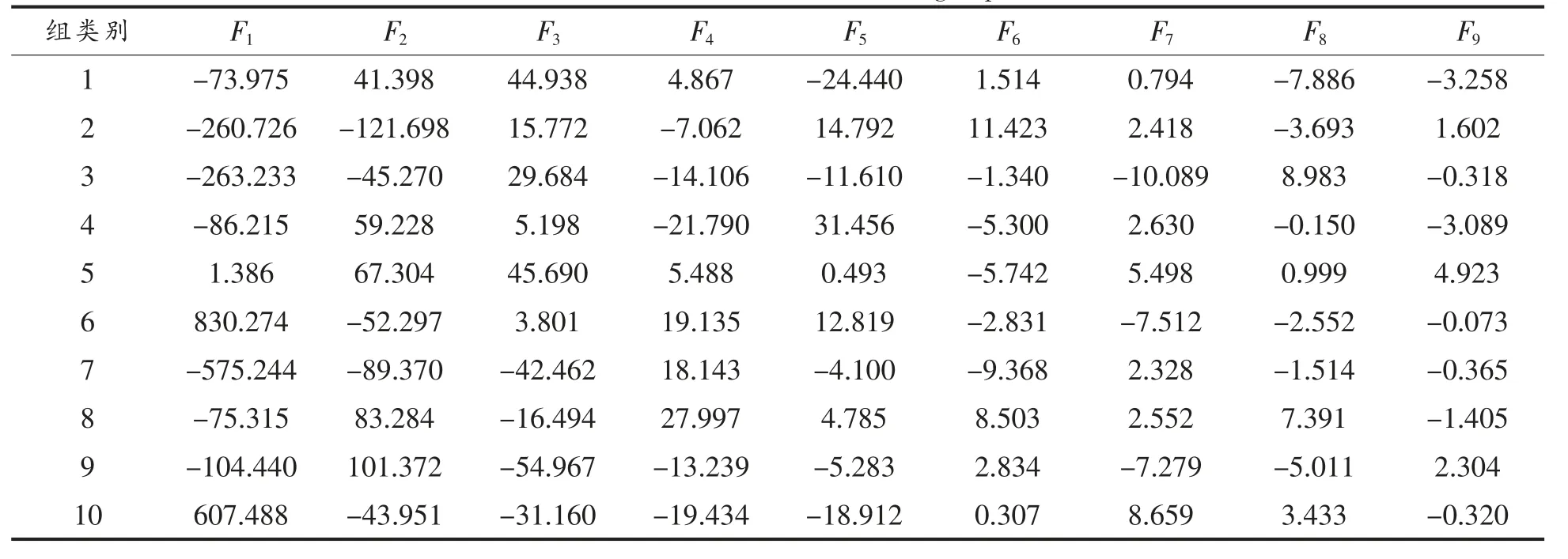
表7 模型M1 中各组质心坐标Table 7 The centroid coordinates of each group in model M1

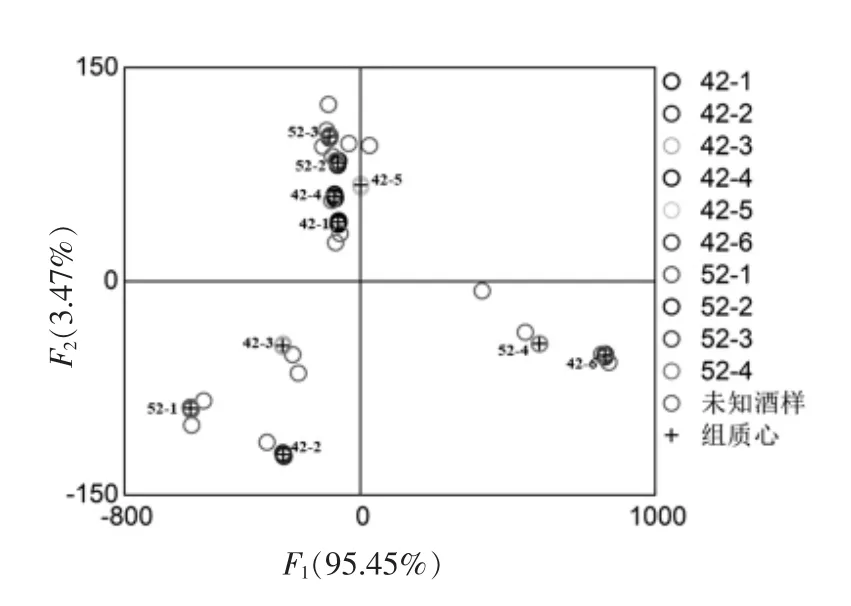
图3 模型M1 的Fisher 线性判别函数散点图Fig.3 The scatter plot of Fisher's linear discriminant function for model M1

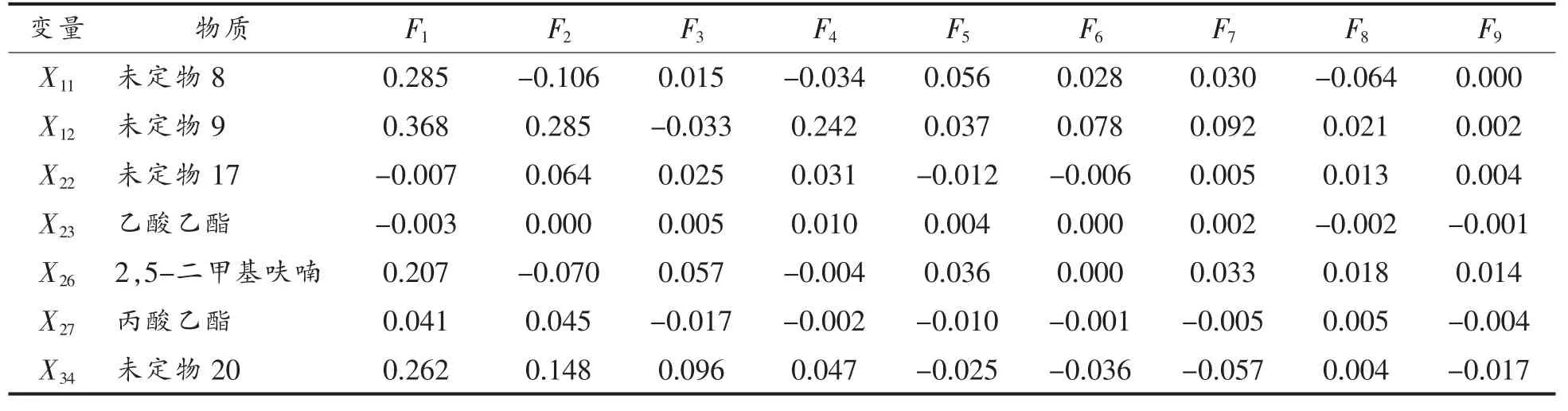
表6 模型M1 的Fisher 线性判别函数系数Table 6 Fisher's linear discriminant function coefficient for model M1

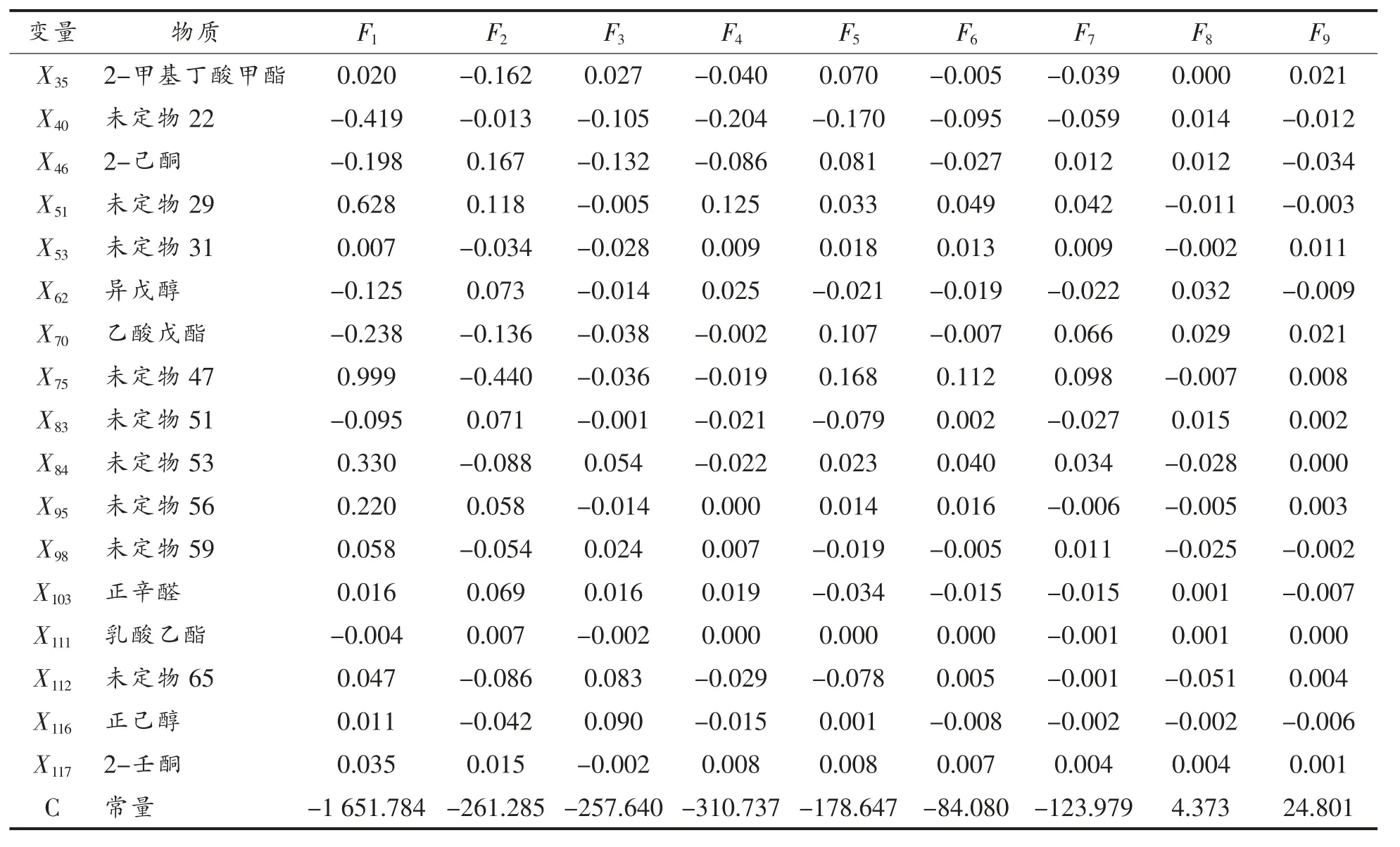
（续表6）

根据表6 中系数建立模型判别函数：

F1= 0.285 X11+ 0.368 X12-0.007 X22+……+0.035 X117-1651.784

F2= -0.106X11+ 0.285 X12+ 0.064X22+……+0.015 X117-261.285

F3= 0.015 X11- 0.033 X12+ 0.025 X22+……-0.002 X117-257.640

F4=-0.034 X11+0.242 X12+0.031 X22+……+0.008 X117-310.737

F5= 0.056 X11+ 0.037 X12- 0.012X22+……+0.008 X117-178.647

F6= 0.028 X11+ 0.078 X12- 0.006X22+……+0.007 X117-84.080

F7= 0.030 X11+ 0.092 X12+ 0.005X22+……+0.004 X117-123.979

F8=-0.064 X11+0.021 X12+0.013 X22+……+0.004 X117+4.373

F9= 0.002 X12+ 0.004 X22- 0.001 X23+……+0.001 X117+24.801

根据Fisher 线性判别函数F1～F9，将未知酒样（测试集）的24 个特征数据代入函数中，计算函数值，即为样本坐标，然后分别计算与10 个组质心的距离，将其鉴别为最近距离的组（G1～G10）。 对测试集酒样鉴别正确率达100%，鉴别结果见表8。

表8 测试集酒样与模型M1 中各组质心距离以及鉴别结果Table 8 The distance between samples in test set and centroids of each group and identification results in model M1

将经相关性分析筛选出的39 个特征采用逐步回归分析拟合21 次，获得最优模型M2。 M2 中采用21 个主要特征，分别为未定物3、5、8、9、10、12、19、33、36、50、53、58、65、69，2，3-二甲基-1，3-丁二烯、 乙酸异戊酯、2-己醇、5-甲基-3-庚酮、2，4，5-三甲基噻唑、 丙酸和癸酸乙酯。 Wilk's Lambda 检验结果P=0.000，说明该模型具有统计学意义。 取9 个判别函数，其特征值分别为8 927.756，1 063.998，269.675，75.069，54.977，19.170，15.420，3.956 和2.795，分别能够解释模型方差变化的85.574%，10.199%，2.585%，0.720%，0.527%，0.184%，0.148%，0.038%和0.027%。 前2个Fisher 线性判别函数共可解释95.772%的方差变化，包含了主要的信息，并可描述各特征的差异与联系。 以前两个Fisher 线性判别函数作散点图（图4）。 图4 中，10 种白酒彼此分隔，同种白酒聚敛十分好，基本以组质心为中心聚拢。与图3 不同的是，图4 中测试集中未知酒样的分布相对混乱，可以预见其对未知酒样鉴别正确率会降低。 该模型对训练集鉴别正确率达100%，采用留一法交叉验证正确率为100%。所建立的模型Fisher 线性判别函数系数见表9，各组质心见表10。根据9 个判别函数计算出的训练集未知酒样坐标并鉴别，其结果见表11。 采用21 个主要特征建立的判别模型对未知酒样鉴别正确率为95%，只有52-4 被错误预测为42-6。

表9 模型M2 的Fisher 线性判别函数系数Table 9 Fisher's linear discriminant function coefficient for model M2

表10 模型M2 中各组质心坐标Table 10 The centroid coordinates of each group in model M2

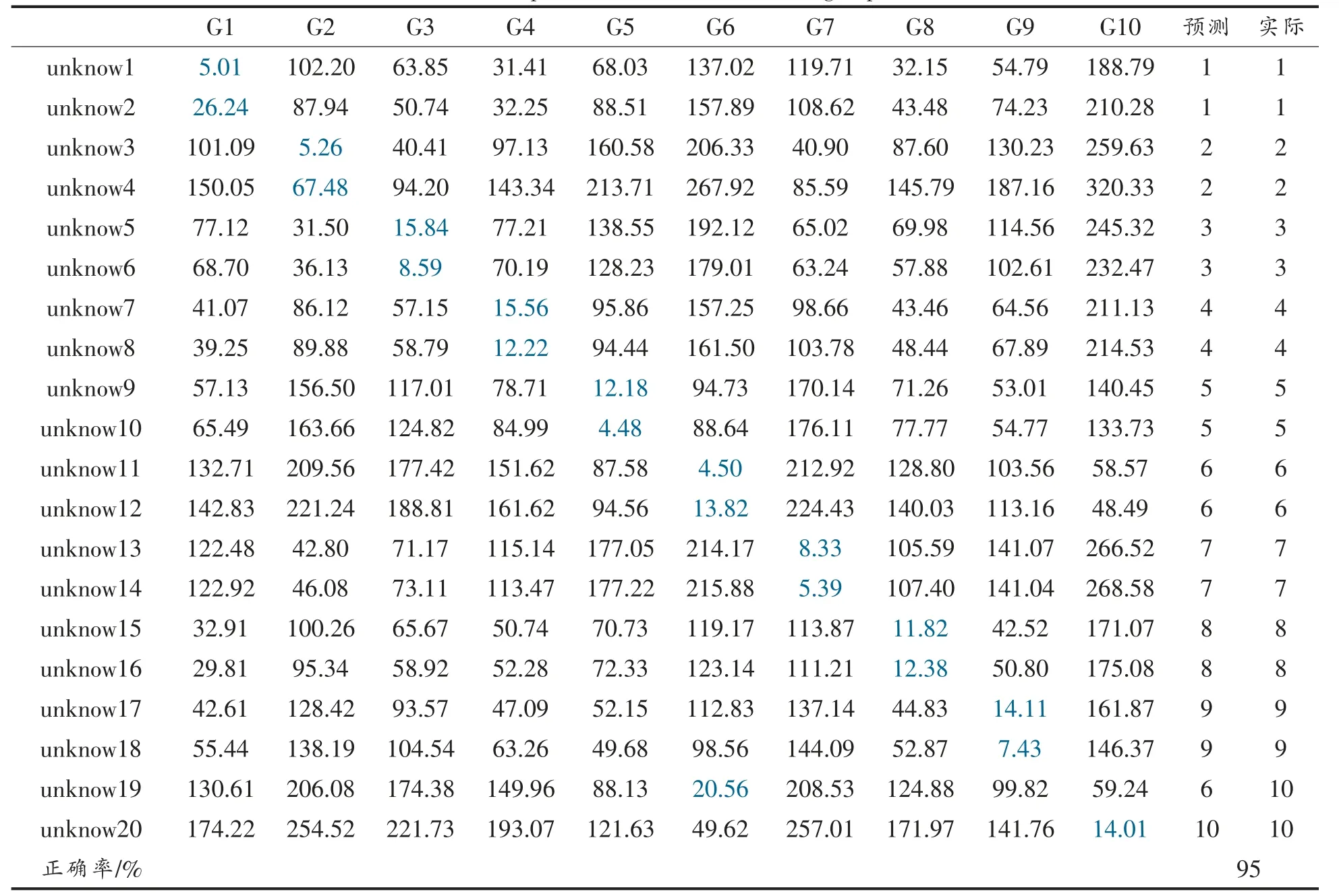
表11 未知酒样与模型M2 中各组质心距离以及鉴别结果Table 11 The distance between unknown samples and centroids of each group and identification results in model M2

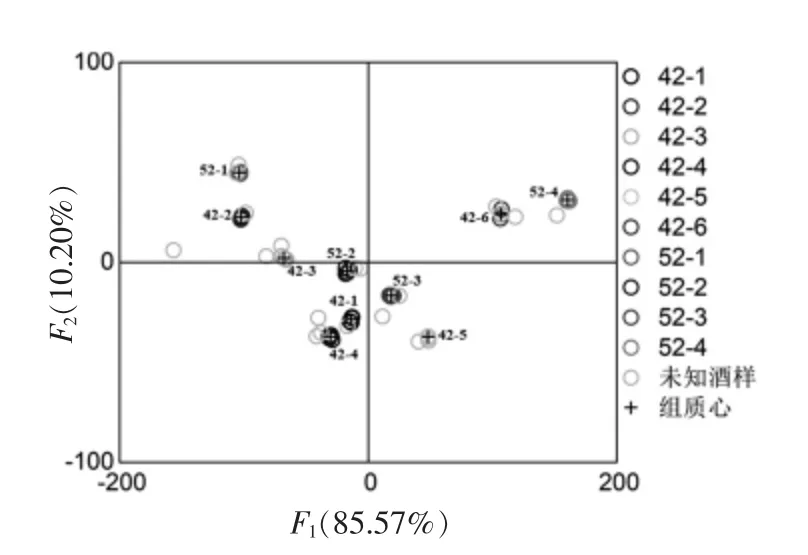
图4 模型M2 的Fisher 线性判别函数散点图Fig.4 The scatter plot of Fisher's linear discriminant function for model M2

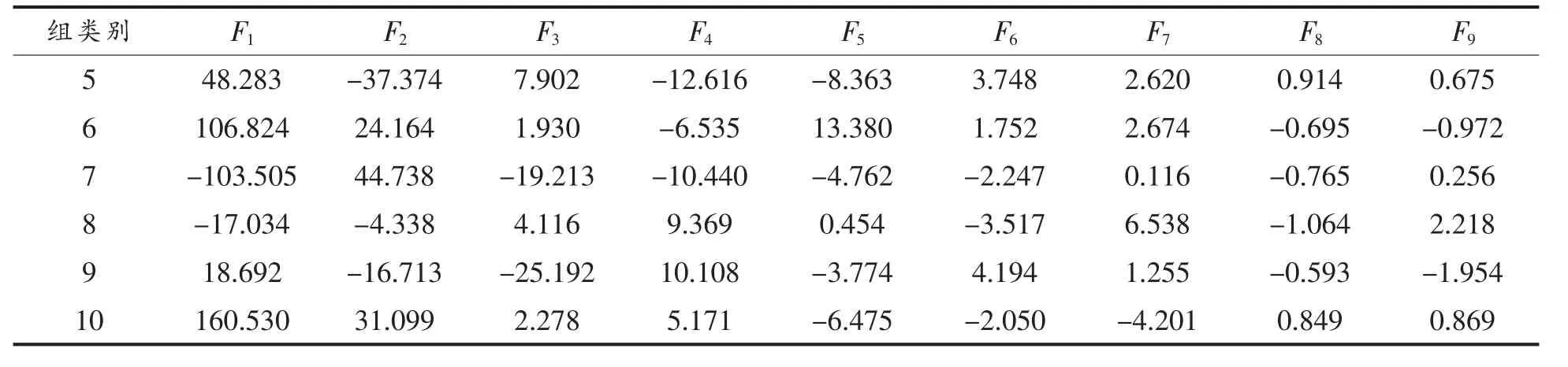
（续表10）

根据表9 中系数建立模型判别函数：

F1= 0.369 X3- 0.055 X5+ 0.553 X8+……+0.007 X134-331.721

F2= 0.011 X3- 0.038 X5+ 0.040 X8+……-0.007 X134-191.563

F3= 0.015 X3+ 0.008 X5-0.127 X8+……-0.004 X130+113.399

F4= 0.047 X3- 0.011 X5- 0.095 X8+……+0.008 X134-76.098

F5= 0.042 X3+ 0.010 X5-0.047 X8+……+0.004 X134-62.262

F6= 0.052 X3- 0.024 X5- 0.101 X8+……+0.002 X134+9.224

F7= 0.005 X3- 0.011 X5-0.083 X8+……-0.003 X134- 171.638

F8= 0.034 X3- 0.016 X5 + 0.063 X8+……-0.004 X134-72.314

F9= - 0.004 X3+ 0.007 X5-0.021 X8+……+0.001 X134- 14.944

此外，采用主成分分析得到的6 个主分量作为建模数据，逐步回归分析拟合结果与直接输入结果一致，对训练集和验证集分类正确率分别为100%和90%，对测试集中未知酒样的鉴别正确率为95%。

本文选取的白酒样本既有香型导致的组分差异，也有勾调批次的差异，具有体系的复杂性。 因此相关性特征选择和主成分分析提取的特征建立的Fisher 线性判别模型，对测试集样品的留一法交叉验证正确率未达到100%。以逐步回归分析从全部特征中提取未定物8、2，5-二甲基呋喃和丙酸乙酯等24 个主要特征建立的Fisher 线性判别模型，其训练集、验证集和测试集分类正确率均为100%；根据相关性筛选出的39 个组分特征数据，经逐步回归分析优化为未定物3、2，3-二甲基-1，3-丁二烯和乙酸异戊酯等21 个主要特征建立模型，其训练集、验证集和测试集分类正确率分别为100%，100%和95%；以6 个主分量建立的鉴别模型，对训练集、验证集和测试集分类正确率分别为100%，90%和95%。 以上结果表明，采用逐步回归分析对判别模型中的主要特征进行优化，全部组分特征中经逐步回归筛选出24 个特征建立的Fisher 判别模型对白酒样品的鉴别效果最佳，其性能上优于预先进行特征提取建立的模型。

3 结论

白酒不经预处理，直接顶空制样进行GCIMS 分析，所得指纹图谱能够直观反映白酒样品间的相似性与组分差异，以及勾调批次的稳定性。通过逐步回归分析提取主要特征可以明显改善Fisher 判别模型的性能。 以全部134 个挥发组分结合逐步回归分析拟合，提取出24 个主要组分建立的Fisher 线性判别模型性能最佳，对训练集分类正确率为100%。采用留一法交叉验证分类正确率也为100%，相比于直接Fisher 线性判别建模正确率提升了82.5%，对测试集中未知酒样的鉴别正确率也达到100%。

GC-IMS 方法无需对微量组分进行定性及定量，依据各物质相对含量即可提取白酒的主要特征，并建立模型实现白酒的准确鉴别。 GC-IMS 检测方法简便易操作，可为白酒生产过程中质量控制、市场监管及白酒原产地保护提供技术支持，为不同地域、 香型以及不同年份的白酒分类鉴别提供参考。