土工格栅加筋土挡墙土压力分析及其计算方法改进

2023-01-11李丽华郑志刚严寒黄少平周鑫隆

西北工业大学学报 2022年6期

李丽华,郑志刚,严寒,黄少平,周鑫隆

(湖北工业大学土木建筑与环境学院,湖北武汉 430068)

加筋土挡墙土压力大小与分布是影响其安全稳定的关键因素，而土压力的分布规律与计算方法一直是加筋土挡墙研究中的难点问题。Chowdhury[1]将数值计算的侧向土压力与模型试验测量值进行对比验证，基于已验证模型对挡土墙深度与土压力变化关系进行研究，确立了挡墙深度与主动土压力之间的归一化关系。Ahmadabadi等[2]基于水平条分法，提出了一种新的针对黏性回填土的加筋土挡墙主动土压力计算方法。Vahedifard等[3]构建了一种分析框架用来计算在非饱和干湿循环条件下挡墙主动土压力，打破了替代分析法中关于破坏机制和应力表示等相关限制。此外，有限元法因其完善的数学理论基础和高效的计算过程，成为了复杂挡土墙在设计中的一种强有力的重要工具[4-7]。大量研究表明，与未加筋土相比，加筋土在强度和刚度等力学性能方面表现更好，土工格栅作为一种柔性材料，是工程中常用的加筋材料，可以降低面板侧向土压力，同时显著改善土压力分布状况[8-9]。若采用传统的极限平衡法来计算加筋土挡墙土压力会使结果较为保守，因此，Allen等[10-11]提出了K刚度法，对挡墙中的筋材负荷计算更为准确。

针对加筋土挡墙和非加筋土挡墙的土压力计算，国内外学者采用了众多研究方法，包括极限分析法、极限平衡法和均匀分析法等。Bathurst等[12]开发出一种新的工作应力计算方法，用于计算加筋土挡墙中的筋材荷载。为研究挡墙水平方向主动土压力的分布情况，Silvestri[13]提出一种与朗肯土压力理论不同的土压力分析方法，并确定了破坏面的方向。Cheng[14]提出在地震荷载作用下确定挡墙侧向土压力滑移线方程解的轴线旋转方法，发现使用迭代分析方法能更易确定被动土压力。Liu等[15]为确定主动土压力，提出一种广义的切向应力系数，结果表明，当切线半径远大于挡墙深度时，主动土压力收敛，但受到土体黏聚力作用，这一重合系数的临界值小于主动土压力系数。李丽华等[16-17]通过Plaxis3D有限元软件建立三维动态压实加筋土挡墙模型，研究了在不同压实宽度和不同加载方式下的加筋土挡墙三维动态响应。此外，通过模型试验对不同加筋情况做了研究，发现在上部荷载作用下挡墙竖向土压力极大值点由加载处逐渐向挡墙面板处移动[17]。

外摩擦角的存在即挡墙面板侧摩响应，在计算挡墙土压力时会产生较大的影响。Fumio等[18]通过模型试验方法对该滑动层进行进一步研究，结果表明，将中等黏性硅脂和0.3 mm薄乳胶膜制作而成的滑动层放置在试件与承台、底板和面板构件之间，整个试样能够接近理想平面应变条件，发生沿侧壁法向的均匀变形。Tatsuoka和Haibara[19]在大面积法向应力下，对砂在不同光滑程度表面之间进行了一系列直剪试验，发现砂与玻璃的摩擦角在6°～9°之间，采用薄胶乳胶膜和硅油润滑层来降低砂的外摩擦角比光滑或抛光硬质板有效得多。Ruiken[20]基于直接剪切试验结果，发现正应力是影响外摩擦角的重要因素。综上所述，加筋土挡墙在使用过程中，填土与挡墙面板之间受到外摩擦角影响，但在以往的研究中未考虑其具体在加筋土挡墙中的影响作用。因此，在考虑到外摩擦角的情况下，对加筋挡墙土压力大小和分布规律的研究需要进一步开展。

本文利用有限元软件建立了加筋土挡墙数值模型，分析了不同工况下挡墙土压力作为挡墙侧向位移函数的变化特征和分布规律。同时，考虑到挡墙面板侧摩效应影响，计算出了土压力系数。最后，根据非极限状态下挡土墙内外摩擦角的发挥程度，对传统土压力计算公式进行了修正。

1 有限元数值模型

本文采用Plaxis2D软件建立加筋土挡墙有限元模型，对加筋土挡墙采用分步施工进行动态模拟，并用前人试验研究数据对该模型进行了参数修订，验证了模型的合理性与有效性。

1.1 模型与边界条件

在理想平面应变条件下，填土平行于侧壁方向发生变形产生抗剪应力，降低外摩擦角的有效方式是降低面板壁面粗糙度。挡土墙模型的高×宽为1 m×1 m(见图1)，面板选用混凝土模块进行分步施工堆砌而成，方向垂直于地面。选取纵向长度1 m的土工格栅作为挡墙加筋材料。

选用平面应变模型，全局疏密度参数设置为细，并对筋材与面板连接位置进行局部加密，共生成25 786个15应力节点单元。

根据现有研究结论[18,21]可知正应力大小是影响砂和玻璃外摩擦角大小的重要因素。根据相关文献[20]，设定外摩擦角为6°进行分步施工模拟。设置固定锚杆水平支撑用来测定挡墙墙趾应力变化，轴向刚度为4 000 kN/m。根据实际工程情况和相关模拟研究，将边界条件设置为：墙体底部固定约束，右侧水平约束，左侧挡墙面板和墙顶为自由端，如图1所示。

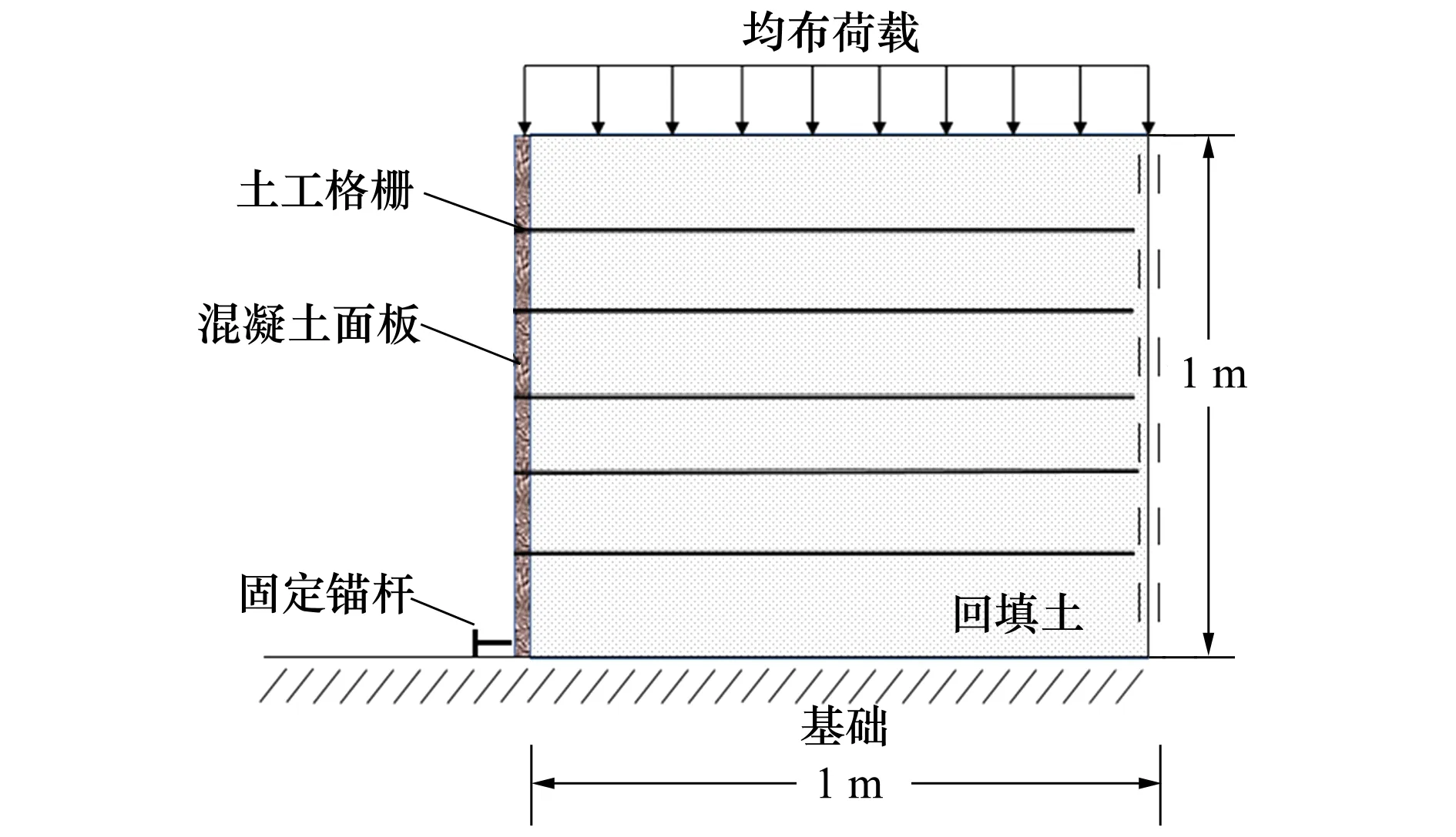
图1 数值计算中模型试件示意图

1.2 材料参数

模型由三部分组成，包括土体单元、土工格栅单元和面板单元。假定结构单元、土体模型和界面之间能够相互兼容，通过设置界面单元来模拟三部分之间的相互作用。填土选用Mohr-Coulomb模型，模块选用线弹性模型，土工格栅选用弹塑性模型进行模拟。本研究采用的土体为干性中砂，相对密度Rd为0.85，表1为具体的土壤参数。

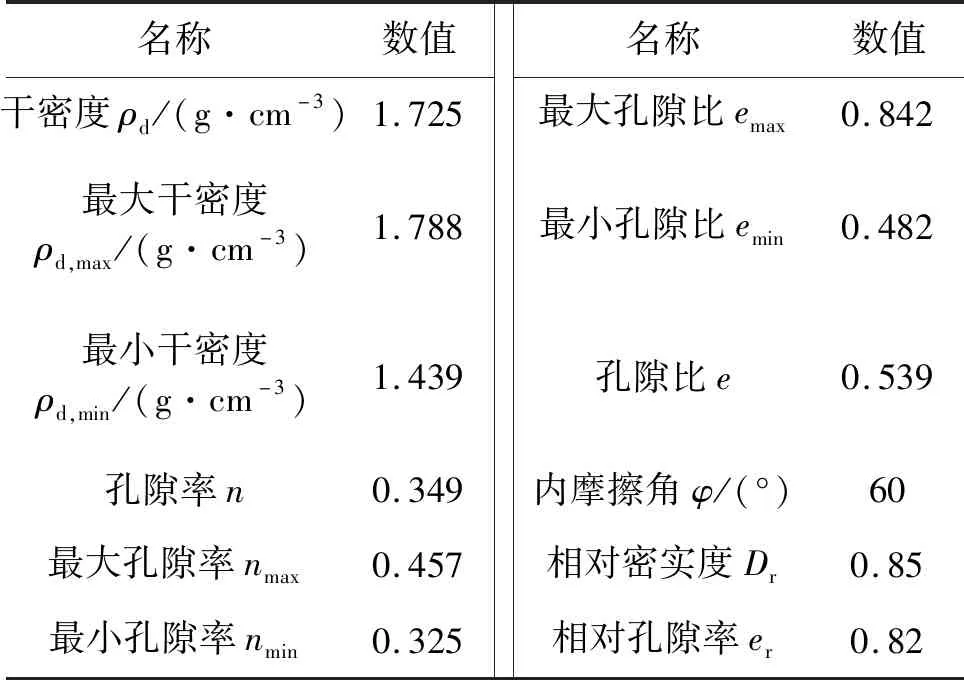
表1 数值模型填土参数

为研究土工格栅抗拉刚度对加筋土挡墙土压力大小和分布规律的影响，本研究选用平均抗拉刚度为700 kN/m的GL-700和1 155 kN/m的GL-1155 2种型号土工格栅。

1.3 模型验证试验设计

针对土工格栅加筋层数对挡墙土压力的影响进行探究。设置6种不同工况进行有限元模拟，筋材均连接到面板承重处，加筋层数和间距如表2所示。

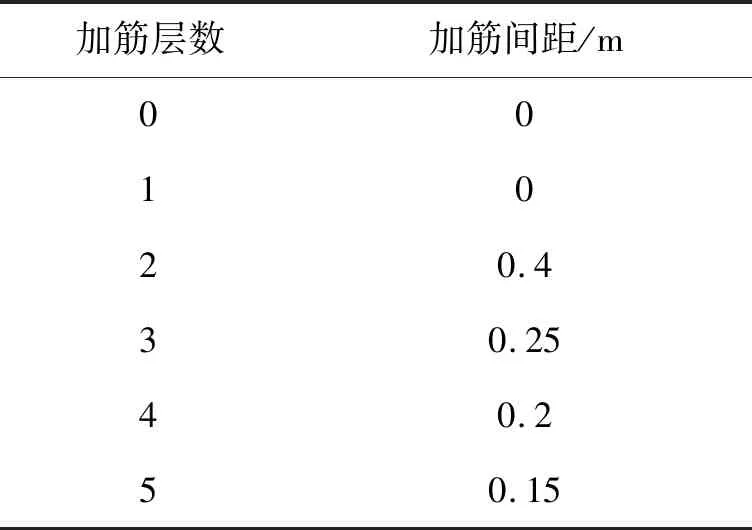
表2 加筋方案设计

缓慢在模型右侧施加Ux/H≤0.01的固定位移，挡墙模型顶部施加50 kPa均布荷载。Ux/H表示墙体横向位移Ux与墙高H的比值，为归一化位移。此次数值试验结果可在一定程度上反映土压力发展规律和分布情况与挡墙变形之间的联系。

有限元试验模拟步骤为：首先在试验开始时，在挡墙顶部施加50 kPa外部压力，然后对挡墙模型缓慢施加右侧位移，在位移施加过程中土工格栅左端与挡墙面板无连接，设置不同的应力点位采集模拟过程中墙体土压力变化情况。

通过文献[21]的挡土墙模型试验验证本文数址模型的有效性，挡土墙模型尺寸为(长×高×宽)1 m×1 m×0.45 m，本文采用的是二维平面应变模型，因此忽略挡墙宽度，挡墙长度和高度则与试验尺寸一致，均为1 m。试验监测仪器主要采用测压元件、土压力盒和LVTD位移传感器，在试验的土压力监测中，挡墙面板上的土压力，由线性滑动轴承处的测压元件测量，挡墙内部土压力通过分层埋置土压力盒测量。

图2为在无筋条件下挡墙模型试验[21]与数值模拟分析结果比较。由图2可知，挡墙土压力模型试验监测数据与有限元数值模拟结果数值大小和随侧向位移变化规律一致，进而验证了该加筋土挡墙数值模型在边界条件设定、网格使用、模型类型和参数选用等方面的合理性和有效性。

数值模拟结果相对实测值土压力略微偏小，这是由于平面应变模型是一个理想模型，没有考虑纵向边界条件。此外，在数值模拟中忽略了土体存在的不均匀性和各向异性等材料特性。

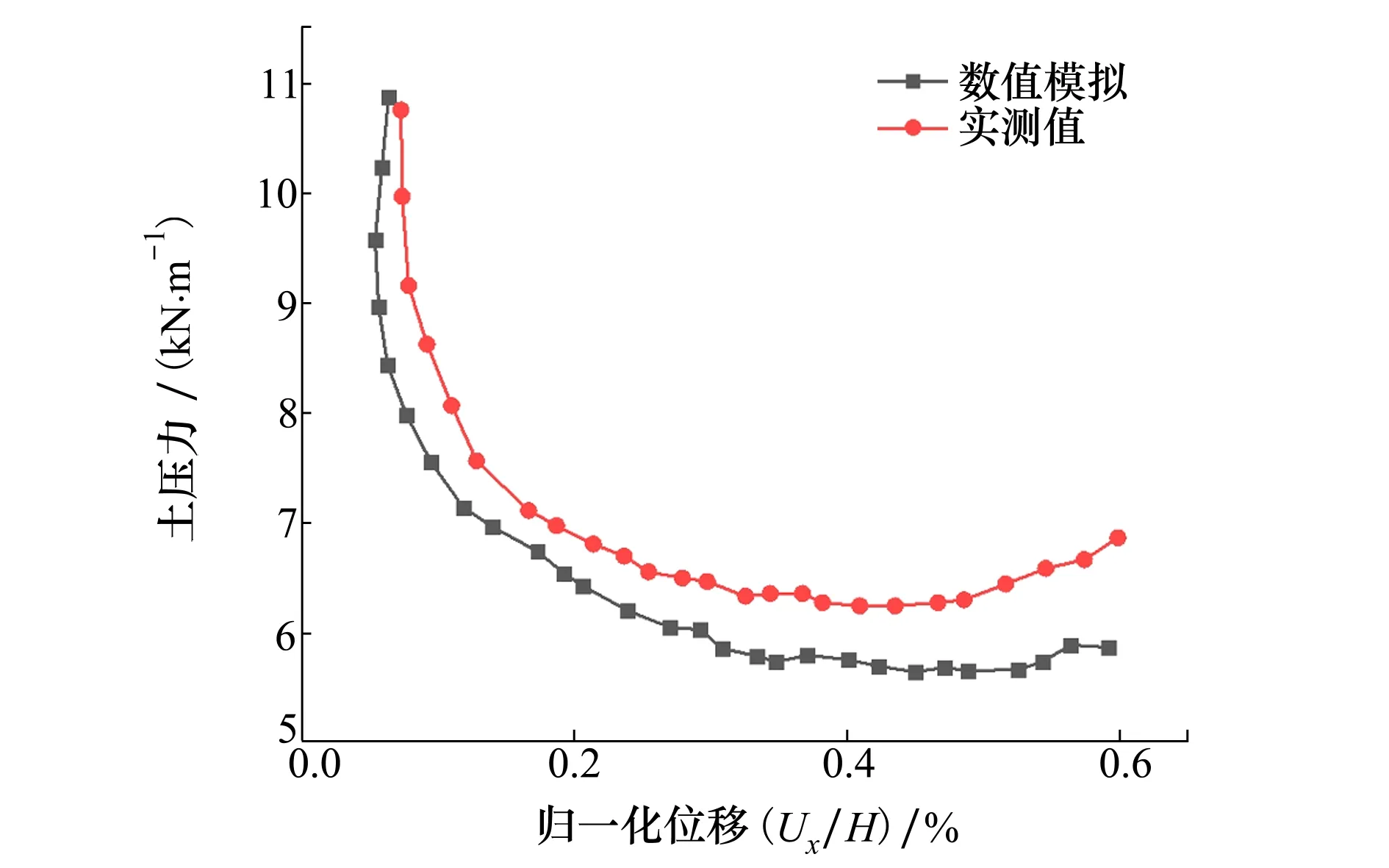
图2 土压力测试值与数值模拟分析结果比较

2 结果分析

2.1 土压力

土工格栅未连接到挡墙面板时，不同工况下GL-700和GL-1155土工格栅加筋土挡墙土压力随墙体位移的变化如图3所示。

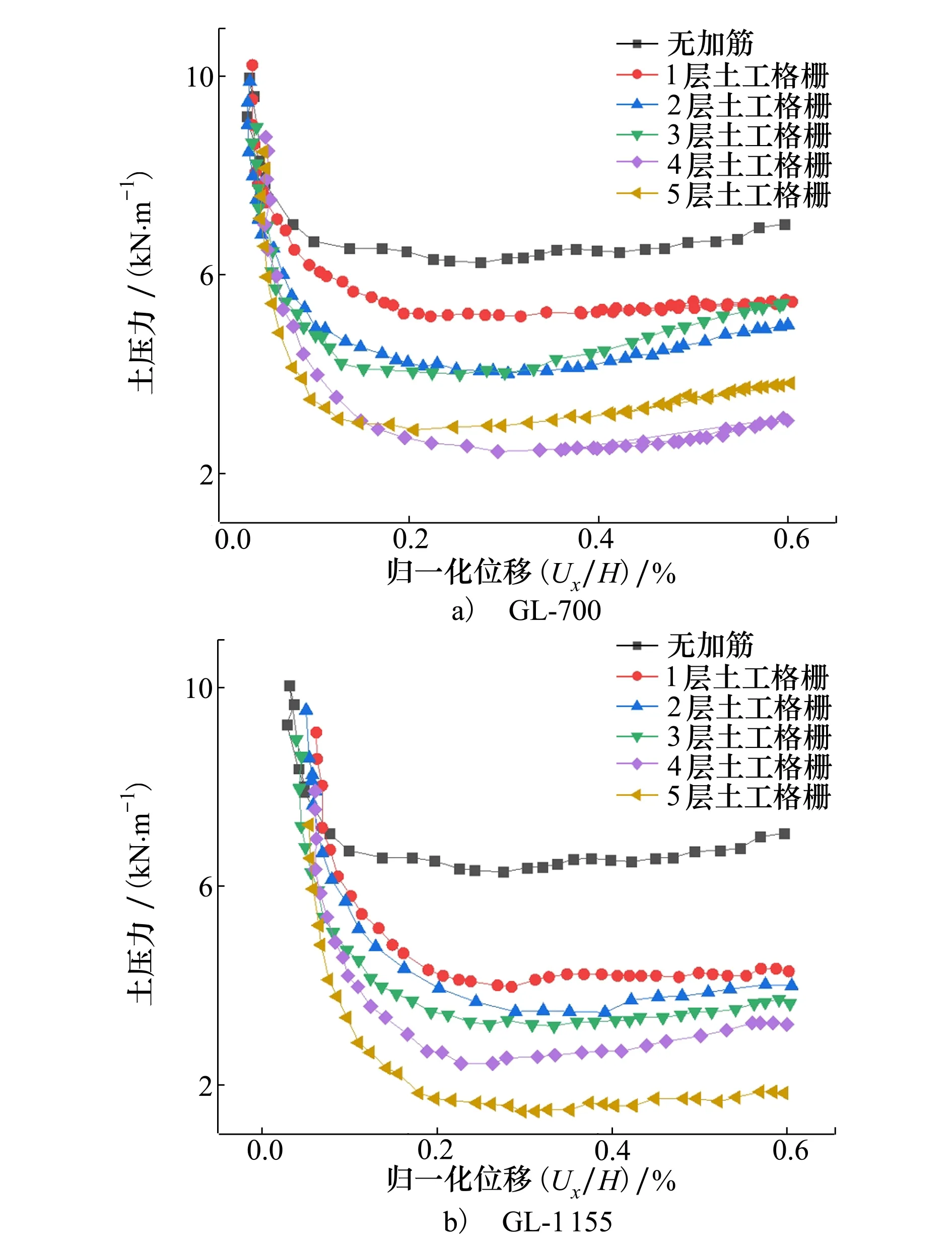
图3 土工格栅加筋土挡墙土压力变化

由图3可知，随着配筋层数增加土压力呈现出逐渐减小的一般趋势，即筋材对土体的加固效应随配筋层数增加而增强，这是由于筋材与填土结合形成了一种复合土体，增强了整体变形能力，将自重和外部荷载产生的应力通过筋材分散到各土层之间，进而减小面板上的土压力。

随着侧向位移增加，不同加筋层数下的挡墙土压力有接近的趋势。这是由于筋材选用的是弹塑性模型，随着试验的进行，土工格栅逐步发挥作用的同时也在发生着塑性变形，导致对土体的加固效果与试验初期存在差异。通过图3a)和3b)可知，后者加筋与未加筋的挡墙面板土压力效果存在显著差异，一层土工格栅加筋比未加筋试件土压力值可减少35%～40%，当采用3层土工格栅对挡墙进行加筋时，土压力值降低40%～60%。土工格栅刚度与挡墙土压力大小呈负相关，这是由于土工格栅不仅能传递应力，自身也可进行应力承担，其刚度越大，承担应力的能力就越强，对土体的加固作用也就越显著。

2.2 土压力分布

为研究土工格栅对挡墙土压力沿高度分布规律的影响，在侧向位移Ux/H=0.2%时，采集了不同工况下加筋土挡墙土压力在归一化高度上的分布，结果如图4所示。

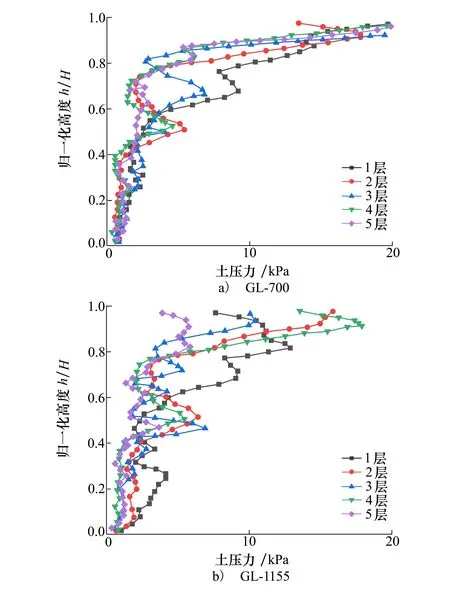
图4 Ux/H=0.2%处不同土工格栅层数土压力分布规律

归一化高度h/H为监测点的竖向高度h与墙高H的比值。从图中可以看出，土压力值与深度总体呈反比。同时，在靠近面板上部附近(h/H=0.8～1.0)，多数工况下挡墙土压力随深度增加反而会增大。主要原因是伴随监测点深度的增加，面板侧壁摩擦逐渐增大，造成在挡墙底部土压力减小趋势明显大于挡墙上部，这也证明了面板的侧壁摩擦效应不可忽略。

加筋土挡墙与未加筋土挡墙相比，前者土压力较小，且加筋层数在挡墙上部对土压力降低影响幅度更为显著，而在挡墙下部，加筋层数差异效果不明显。而对比2种土工格栅(GL-700和GL-1155)发现，亦呈现上述规律，土工格栅刚度在挡墙上部对土压力数值大小影响较大，而在挡墙底部刚度差异带来的加筋效果差异不明显。造成这种效果的原因可能是每个模型试样的外摩擦角设置均为6°，在挡墙底部，填土与面板侧摩效应明显对土压力的减小效果显著，分担了由加筋层数和加筋刚度不同所带来的差异。

图5展示了2种工况下土工格栅与挡墙面板采用不同连接方式时的挡墙土压力沿归一化高度h/H的分布情况。图5a)为单层加筋，图5b)为双层加筋。可以发现，土工格栅与面板连接与否对挡墙土压力的数值大小和分布规律影响不大，但相关文献表明[22]，筋材连接方式对土体的塑性变形会造成较大影响。这是由于受到竖向外部荷载作用，土体与筋材牢牢地嵌合在一起，这种嵌固作用远大于挡墙面板对筋材的限制，所以筋材与面板连接与否对挡墙土压力不会造成显著影响。

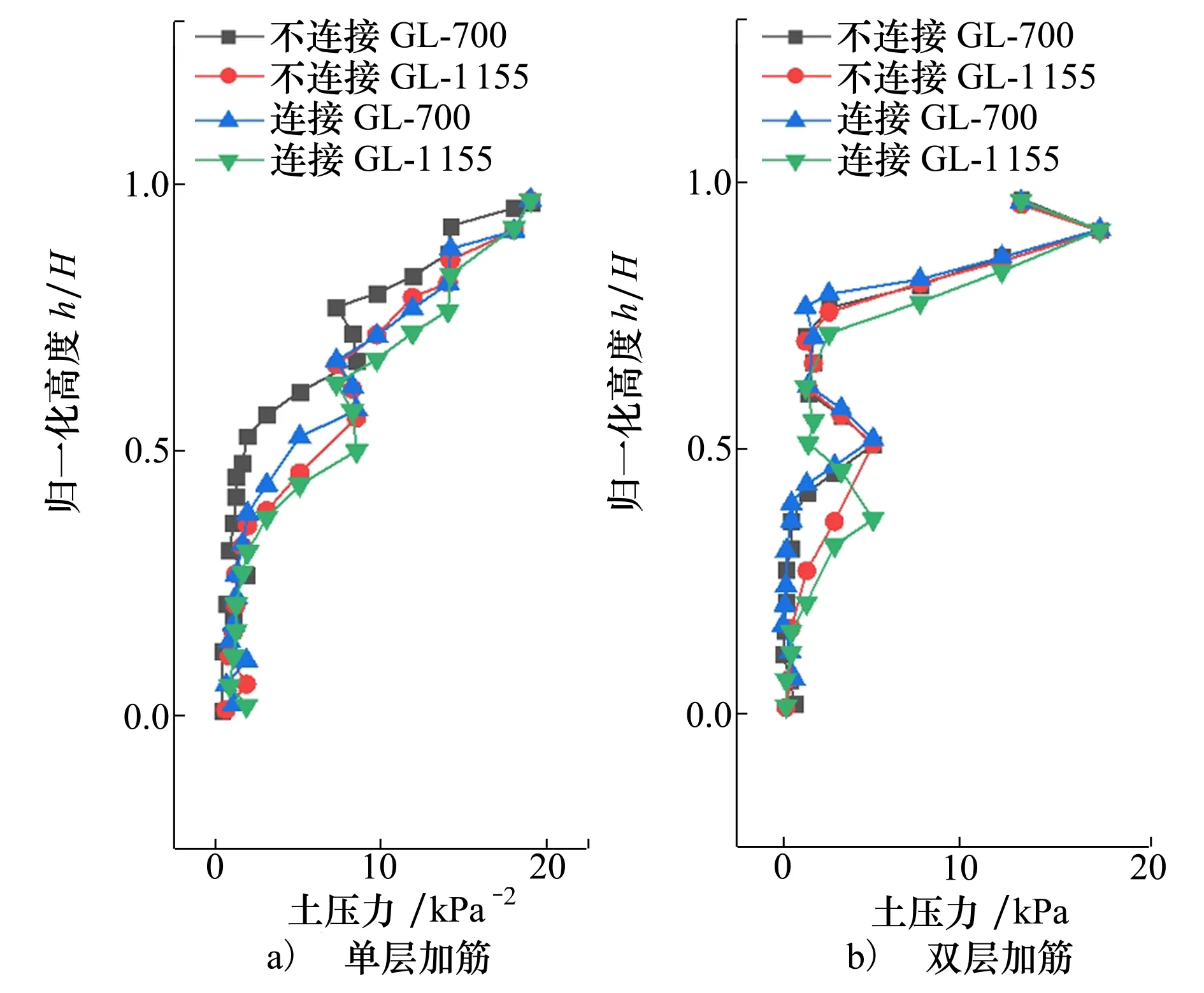
图5 不同土工格栅与面板连接方式的加筋土挡墙土压力分布(Ux/H=0.2%)

图6展示了在非加筋工况下土压力模拟结果与是否考虑外摩擦角理论计算结果对比。在图6中计算出土压力系数Ka后，理论土压力仅随深度z变化，在图中呈直线分布。挡墙顶部侧壁摩擦较小可忽略，因此2种理论土压力计算结果均在挡墙上端收敛。试验侧向位移施加过程中土压力系数测量值由K0表示，K0=0.47时，侧向位移Ux/H=0.005%～0.01%，表示处于静止土压力状态。q0=50 kPa的外部荷载作用下，土压力系数明显下降。结果表明，有限元模拟方法在试验中能较好反映侧壁摩擦，由于未对挡墙加筋，减小的土体应力认为与加筋状况无关而是由侧摩效应所导致的。

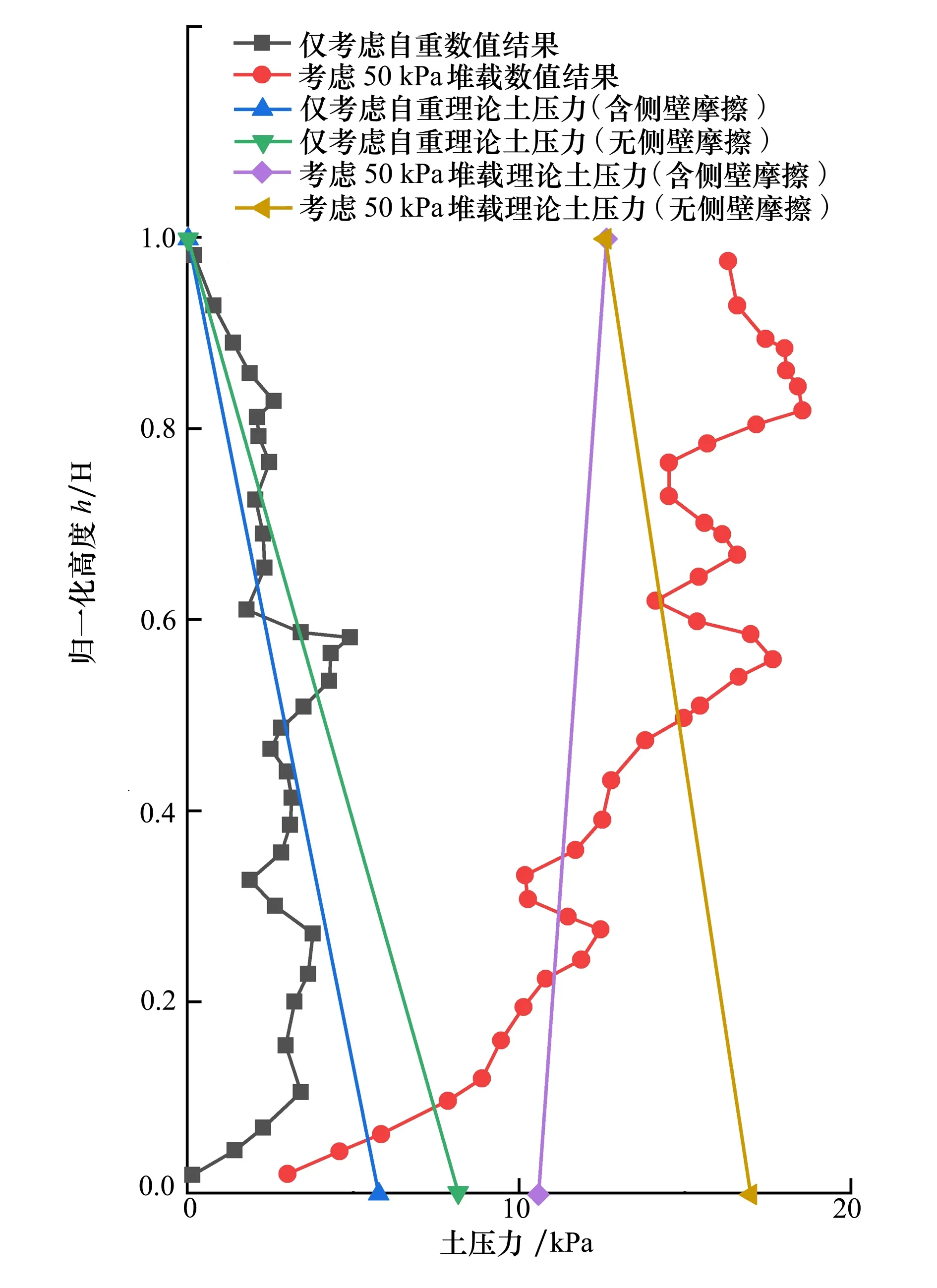
图6 是否考虑边墙摩擦情况下静止状态下的实测土压力和理论土压力

2.3 考虑侧壁摩擦效应应力分析

Bathurst和Benjamin[23]研究发现，竖向应力随自重逐渐减少

g′(z)=γ×z(1-2×Ksw×tanδsw)

(1)

式中:土体重度γ=17.1 kN/m3;z表示距挡墙顶部距离;δsw表示竖向应力下砂土与面板之间的外摩擦角。

面板与填土之间的土压力系数为Ksw=K2/2(1+Ka),应力σ2在平面应变中土压力系数K2=0.7[24],在土压力系数基础上进行迭代,可选取主动土压力系数Ka=0.47。

侧摩效应可降低由外部荷载引起的垂直应力。在理想条件下,用Bathurst和Benjamin[23]的公式描述

q(z)=q0×e-C1×z

(2)

式中，q0为外部竖向荷载。

C1=2×Ksw/W×tanδsw

(3)

式中:挡墙宽度W=0.45 m,同等应力水平下土体与侧壁之间的摩擦角δsw=15°。

根据侧摩效应所调整后的总有效应力为

(4)

2.4 土压力系数

通常根据土压力理论来设计加筋土挡墙面层,土压力系数须考虑到筋材对土体的加固作用。考虑面板侧摩效应时,土压力系数可由总土压力与竖向的平均有效应力比值计算

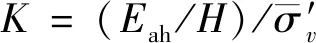
(5)

式中:Eah为水平土压力;H为挡墙高度;σv为根据面板侧摩效应获得的总有效应力。

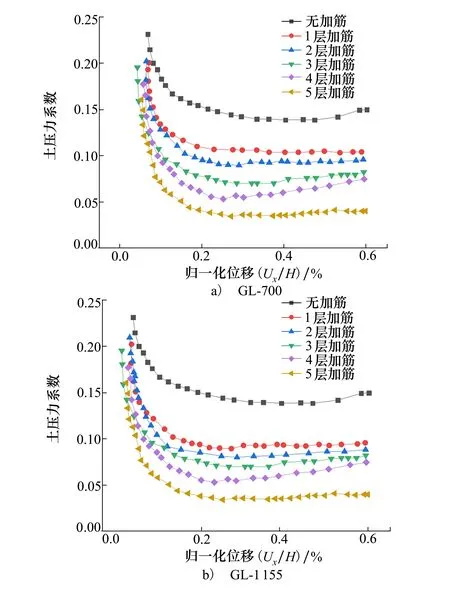
图7 不同刚度土工格栅加筋土挡墙土压力系数随侧向位移变化关系

图7展示了不同工况下筋材与面板无连接时土压力系数随侧向位移的变化曲线。图7a)～7b)分别展示了2种不同筋材(GL-700和GL-1155)的情况。

从图7中可以看出,在经历试验的初期阶段(Ux/H=0.02%),主动土压力系数数值较低。而若不考虑挡墙面板的侧摩效应,该值会更高[25]。另外,挡墙土压力降低主要在Ux/H=0.1%处发生。

3 土压力计算公式改进

由于在土压力产生过程中,侧摩效应会产生较大影响,而现在常用的朗肯土压力方法虽然较为简单,但假定忽略了侧壁摩擦效应,而在土体到达极限状态之前的土压力变化比较复杂,库伦土压力计算过程相对又过于繁琐,因此提出一种在非极限状态下能考虑侧壁摩擦效应的土压力计算方法是非常有必要的。

3.1 公式推导

当前,计算挡墙土压力方法一般采用假设土体处于极限状态下的经典土压力理论。现有研究[26]发现,挡墙工作时,墙后土体多数为非极限状态,尤其是挡墙处于主动状态下时,极限状态下土压力通常小于非极限状态下土压力。

在经典土压力理论中,土体内摩擦角为常数,而在工程实际中,土体内部摩擦和土-墙之间的侧壁摩擦通常是随着变形而逐步形成,大量现场检测和试验研究表明[27],土压力呈非线性分布。

随着土压力逐渐增大,墙后填土逐渐由静止状态向极限状态过渡,内摩擦角渐渐发挥作用。因此,将内摩擦角作为一个常数处理并不符合实际情况。土体内摩擦角发挥值φm通过(6)式计算

(6)

式中:Kd表示影响系数,反映了φm受到位移量S的影响程度;Sa是土体塑性破坏时的水平位移量,可对应表3情形进行取值。φ0根据(7)式可求解

K0=1-sinφ

(7)

当墙体发生位移变形时,有可能导致填土发生相对墙体的偏移,水平应力会相应改变,直到与墙体产生塑性平衡,转变成主动极限状态。因而,水平方向的主动土压力σam可表示在特定位移下静止土压力σ0与松弛土压力σr的关系

σam=σ0-σr

(8)

当挡墙发生转动,墙后填土进入主动极限状态时,水平土压力σam与库伦土压力σa的关系为

σam=σacosδ

(9)

松弛应力σr到达最大值,引入位移函数Fa,使σr=Faσrmax,即

σam=σ0-Fa(σ0-σacosδ)

(10)

Fa如(11)式所示

(11)

将σ0=K0γh,σa=Kaγh和Ka代入(11)式,即可得出非极限状态下的土压力系数Kam

(12)

3.2 模型验证

为验证该公式的合理性，图8展示了传统Coulomb理论、有限元模拟和3.1节改进公式对土压力系数计算结果与实测结果[21]对比。

从图中可以看出，在3种不同的内摩擦角下，Coulomb理论解对土压力计算偏保守，与实测值偏差较大，尤其在侧向位移刚施加阶段，Coulomb理论计算出的土压力系数远远小于实测值。与其相比，改进公式土压力系数随着位移的施加在数值和变化趋势上都更接近实际情况。

当内摩擦角φ为50°和62°时，改进公式计算结果和实测值均出现极大值点，随着位移的施加，由之前的上升趋势转变为下降趋势。这可能是由于在较大内摩擦角作用下，随着试验的进行，内摩擦角发挥作用的空间较大，导致试验初期出现土压力系数上升的情况。而这种现象在另外2种计算结果中均未体现。这说明本文基于土体在非极限状态下所提出的土压力计算方法，由于考虑土体处于非极限状态和墙壁侧摩效应，对主动土压力大小和分布的计算较为准确、合理。