筋材布置方式对加筋土挡墙地震稳定性的影响
2023-01-03朱玉明贾世林戴光宇
朱玉明, 张 飞, 贾世林, 戴光宇
(1. 河海大学 岩土力学与堤坝工程教育部重点实验室,南京 210098;2. 河海大学 岩土工程科学研究所,南京 210098)
加筋土技术历史悠久,良渚古人5 000年前利用黏土与稻草制成的“草裹泥”方法修筑堤坝[1];2 000年前的汉朝,人们利用稻草建造长城,历经千年仍屹立在西北戈壁[2]。近代随着新型土工合成材料的问世,新型加筋土技术被大量应用于挡土墙建设中,取得了显著的经济和环境效益。我国于20世纪70年代在云南田坝矿区建成了国内第一座加筋土挡墙,随后该技术被大量使用在土木、水利、交通等诸多领域的工程中,目前我国已建成近千座的加筋土挡墙。
大量加筋挡墙震后调查[3-5]已充分证实,土工合成材料加筋土挡墙不仅在静力条件下表现出了良好的工作性能,同时在地震条件下也表现出良好的抗震性能[6]。由于加筋土挡墙在地震作用下力学性状复杂,现有基于土压力理论的抗震设计方法仍存在不足,还有一些加筋土挡墙发生地震破坏的情况,如1999年我国台湾地区集集地震中某公路沿线的模块式加筋土挡墙[7]、2008年汶川地震中国道G213某加筋土挡墙[8]均发生变形破坏。现有地震作用下加筋土挡墙性状研究多采用试验[9-11]或数值模拟[12-13]法,现行规范[14-17]多使用土压力理论作为加筋土挡墙设计方法,但由于地震作用的不确定性,现行规范分析方法可能导致加筋土挡墙安全储备不足。极限平衡法可以很好的反映极限状态加筋挡墙内部性状[18],适用于地震作用下加筋土挡墙性状分析,Leshchinsky等[19]和Han等[20]基于极限平衡法分别采用对数螺旋线和直线破坏模式计算了加筋土挡墙静力极限状态的稳定所需加筋力分布。拟静力法[21-22]或拟动力法[23]是常用的地震加筋土挡墙稳定性分析理论,杨有海[24]在国内较早使用拟静力法研究水平地震作用对加筋土挡墙的影响,蒋建清等[25]运用拟静力法在已有水平条分法[26]的基础上研究了不同破坏面形状对加筋土挡墙地震稳定性的影响,程亚男等[27]克服拟静力法的局限性,运用拟动力法进一步研究了加筋土挡墙地震响应特性。
为了确保加筋土挡墙地震安全性,现行规范推荐设计考虑适当加长筋材长度,再对地震工况进行稳定性校核来满足抗震安全设计要求,这样可能会造成材料浪费和成本增加。Leshchinsky[28]提出在加筋土挡墙主筋之间布置短筋来减小墙面变形和分担主筋所受拉力,随后Jiang等[29-30]运用数值模拟方法和现场试验对短筋布置方式进行了深入研究,进一步验证了其有效性。但是这种短筋布置方式还仅限于静力条件,鲜有考虑地震情况。Watanabe等[31]通过振动台模型试验证实了局部筋材加长可以提高加筋土挡墙地震稳定性,但尚未探明筋材加长位置和长度对加筋土挡墙地震稳定性的影响规律。因此,本文将运用极限状态下加筋土挡墙稳定所需加筋力计算方法,考虑地震作用开展不同筋材布置方式(如单层加长、双层加长、短筋布置、变间距布置)下的加筋土挡墙稳定性分析,从而揭示筋材布置方式对加筋土挡墙地震稳定性的影响规律,以期能为加筋土挡墙抗震设计提供新思路。
1 地震作用下加筋土挡墙稳定所需加筋力计算方法
1.1 极限状态下地震加筋挡墙受力分析
土工合成材料加筋土挡墙属于柔性支挡结构,相对于传统支挡结构(如重力式挡墙、悬臂式挡墙和扶壁式挡墙等)其抗震性能更好[32-34]。振动台模型试验[35]结果表明:土工合成材料加筋土挡墙在地震作用下,最危险滑动面趋于楔形直线模式。本方法采用直线破坏假设对土工合成材料加筋土挡墙地震稳定性进行拟静力分析,建立地震加筋土挡墙稳定性受力分析模型,如图1所示。
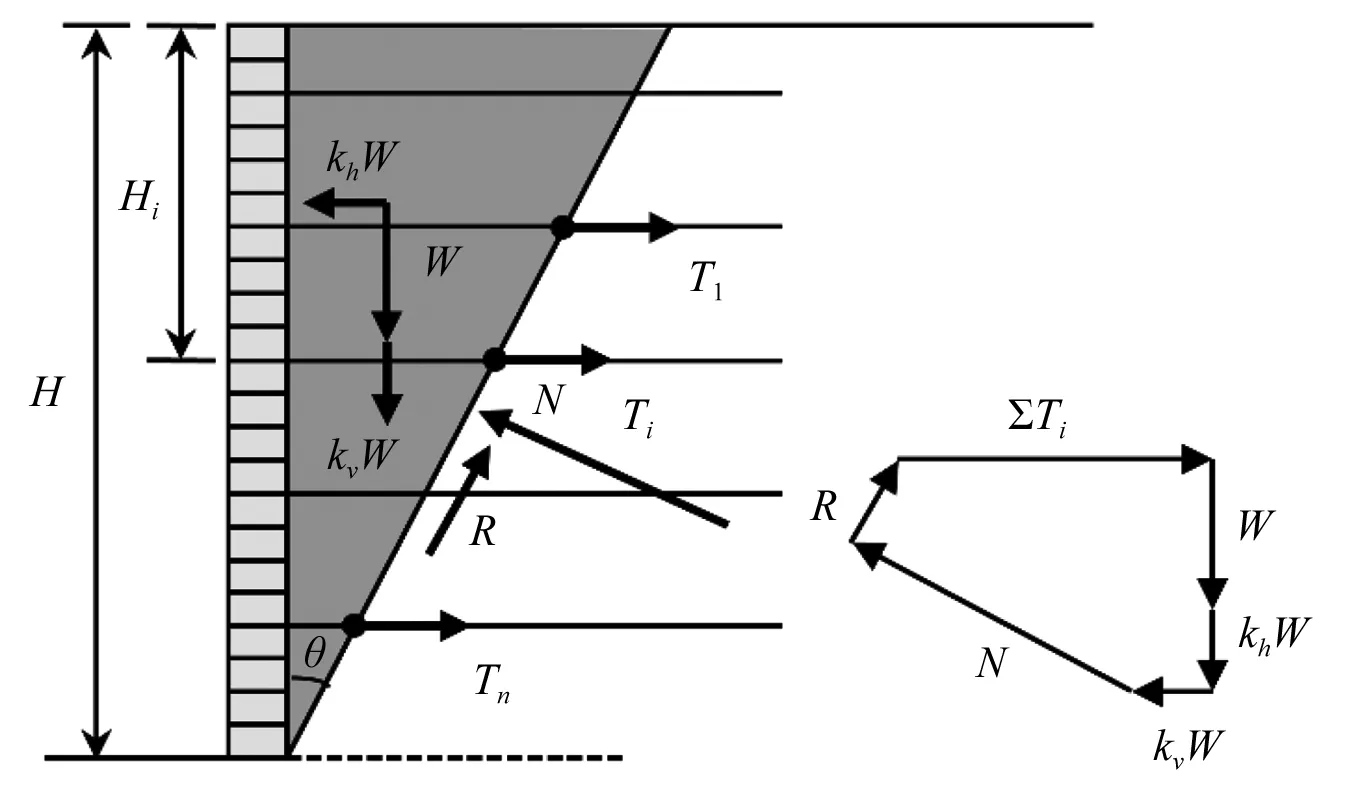
图1 加筋土挡墙受力分析及矢量平衡示意图Fig.1 Mechanical analysis and force vector equilibrium of GRS walls
针对该模型建立沿滑动面和垂直滑动面方向力的平衡方程,根据摩尔-库仑破坏准则,获得各层筋材所需加筋合力∑Ti

(1)
式中:Rc为筋材覆盖率(其意义是筋材单元体宽度与两个筋材单体间距的比值);Rc取值在0%~100%,当没有筋材铺设时,Rc=0,反之,当筋材满铺时Rc=100%; ∑Ti为所有筋材提供的总加筋力;kh为水平地震加速度系数;kv为垂直地震加速度系数;γ为填土的重度;φ为填土的内摩擦角;θ为滑动面与竖直墙面夹角;Hi为加筋土挡墙墙顶到某一滑动面滑出点的高度。
1.2 极限状态地震加筋挡墙稳定所需加筋力计算
为了实现加筋土挡墙筋材稳定所需加筋力的逐层计算,本文有以下假设:①忽略面板间摩擦作用、面板与填土间摩擦作用、面板弯矩以及墙趾抗力作用对土工合成材料加筋土挡墙稳定性的影响;②各层筋材对维持挡墙稳定有相同贡献;③极限状态为墙后填土先充分发挥其强度达到极限破坏状态、即安全系数FS=1.0;④土工合成材料加筋土挡墙的填土采用无黏性土;⑤拟静力法模拟地震作用,未考虑地震波频率和周期等因素的影响。
运用式(1)可以获得极限状态下加筋土挡墙稳定筋材所需总加筋力,结合假设②将总的加筋力平均分摊到滑动面穿过的每层筋材,由此便可以实现自上而下的逐层加筋力计算。具体步骤如下:①计算第一层筋材(最上层筋材,筋材1)的加筋力分布,将筋材1划分为若干小单元,依次计算由筋材2与面板交汇点作为滑出点滑出并穿过筋材1每个小单元的直线破坏面,如图2(a)所示。式(1)可用以计算并获得沿筋材1长度方向的加筋力分布;②计算筋材2的加筋力分布,同样将筋材2划分为若干小单元,考虑所有从筋材3与面板交汇点位置作为滑出点的破坏面,将式(1)计算结果平均分摊到每层筋材(筋材1和筋材2),此时需要注意对于筋材1还需要与步骤①计算结果对比并保留最大值在对应小单元内,考虑到力的平衡筋材2相应位置内力需要等量减小,如图2(b)所示。重复步骤①和步骤②,直到计算出所有筋材沿长度方向加筋力的分布。
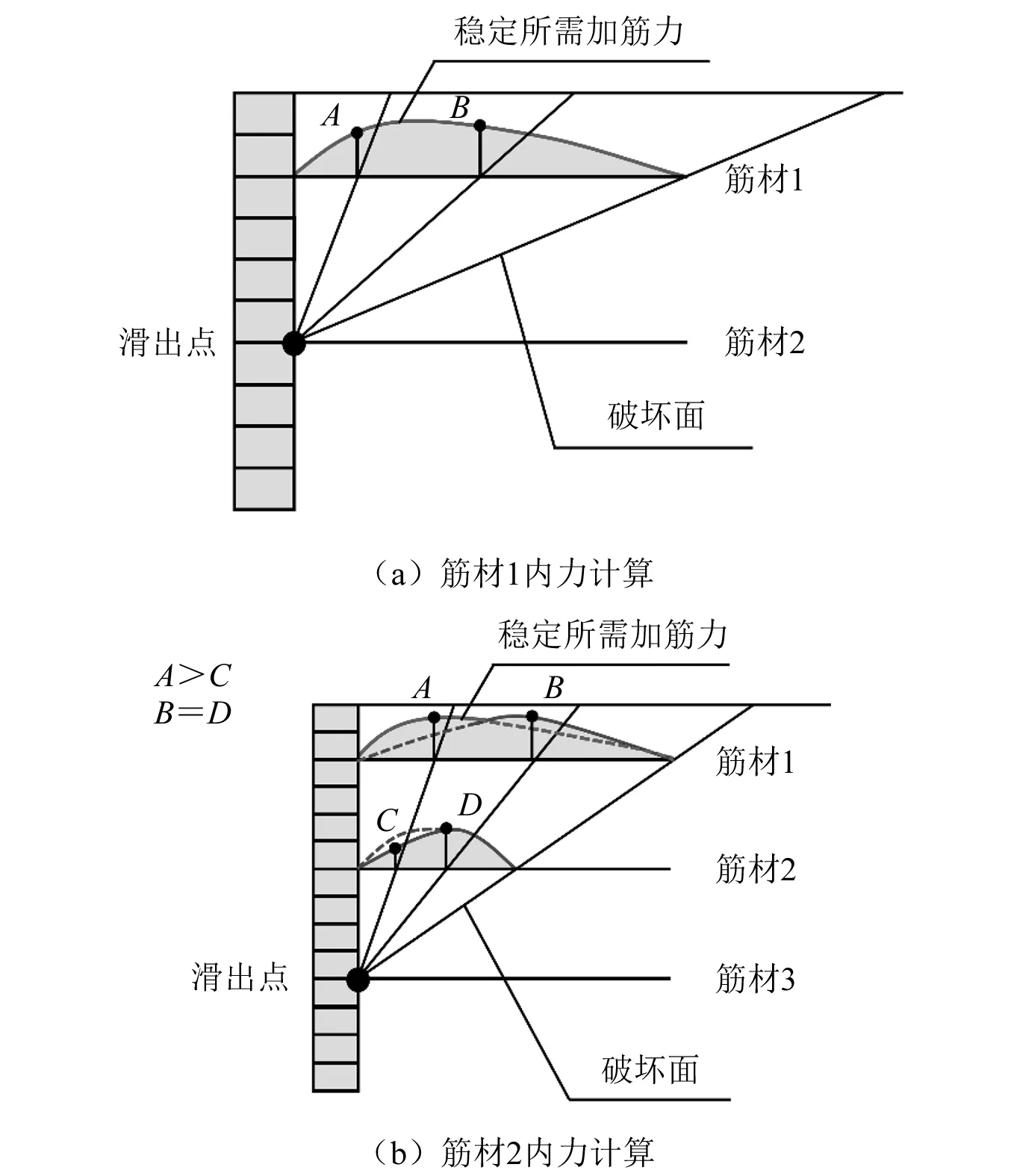
图2 筋材加筋力逐层计算Fig.2 Calculated reinforcement load of GRS walls from top to down
为了防止土工合成材料加筋土挡墙在地震作用下发生前端或后端拔出破坏,各层筋材加筋力在计算过程中需要补充限制条件以确保筋材加筋力在其前后端有足够强度储备,不会在实际工作过程中发生拔出破坏。加筋体通过与土体之间的摩擦实现稳定土体的作用,因此筋材前后端抗拔强度表达式分别为
Tpo(F)-i=To+2xiγziCiRctanφ
(2)
Tpo(E)-i=2(L-xi)γziCiRctanφ
(3)
式中:To为第i层筋材与面板之间的连接力,当xi=0时,式(2)计算出的结果为面板连接力;xi为破坏面与第i层筋材交汇点到墙面的距离;zi为土工合成材料加筋土挡墙中第i层筋材到墙顶的垂直距离;L为筋材布置长度;Ci为筋土界面摩擦因数,对于土工格栅取值为0.8。
结合前后端抗拔强度包络线对挡墙稳定所需加筋力进行调整,对于筋材前端加筋力分布需要依据式(2)进行调整,使调整后的前端拔出强度包络线与极限状态筋材所需加筋力包络线相切,此时面板连接力To即为前端抗拔强度包络线与竖轴的交点,如图3所示。对于筋材后端加筋力分布则需要根据式(3)进行调整,从图3可知,最为理想的情况、即后端抗拔强度包络线与极限状态筋材所需加筋力包络线相切。若出现两包络线相交的情况,超出部分抗拔力需分担到下方筋材加筋力中,如若到最底筋材仍然无法承担所有上部超出的抗拔力,则需要适当增加筋材长度进行重新计算与调整。最终,依据本文计算方法可以获得不同筋材层中的最大加筋力max(Tmax),将计算获得的最大加筋力max(Tmax)与不同型号筋材对应的长期设计强度Tal(Tal为筋材极限抗拉力Tult折减后的结果)进行对比,确保max(Tmax)≤Tal便可以实现加筋土挡墙内部稳定性的设计。
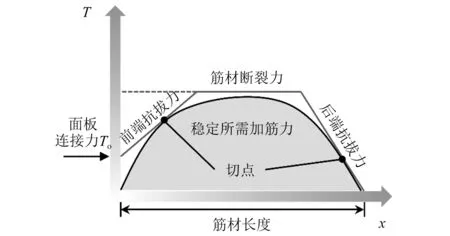
图3 筋材加筋力分布与前后端抗拔强度关系Fig.3 Relationship between required tensile force and front/rear pullout capacity
1.3 方法验证
根据1.2节所述方法编制计算程序,针对Han等所分析的静力状态加筋土挡墙算例进行计算。该模型墙高H=3 m,筋材布置间距Sv=0.6 m;加筋区填土采用无黏性土,重度γ=20 kN/m3;土工格栅筋土界面摩擦因数Ci=0.8,筋材覆盖率Rc=100%。当L=1.8 m时的各层筋材加筋力分布,如图4(a)所示。对比分析结果表明本文与Han等研究的结果基本吻合。当内摩擦角φ=20°时加筋土挡墙各层筋材加筋力分布,两者结果同样较为吻合,如图4(b)所示。Han等研究中给出的静力条件验证结果相一致。
为了进一步验证本文方法在地震条件下的有效性,运用本文方法计算获得Bhattacharjee等[36](原型墙高H=6 m,筋材长度L=4.2 m,填土重度γ=16.2 kN/m3,内摩擦角φ=45°,峰值加速度0.3g,采用拟静力法计算kh取为0.15)和Huang[37](试验模型墙高H=0.60 m,筋材长度L=0.42 m,填土重度γ=15 kN/m3,内摩擦角φ=44°,峰值加速度1.72g,采用拟静力法计算kh取为0.86)所研究加筋土挡墙的破坏面位置并与数值分析结果与模型试验结果对比,如图5所示。结果表明本文方法预测破坏面位置与文献结果较一致。
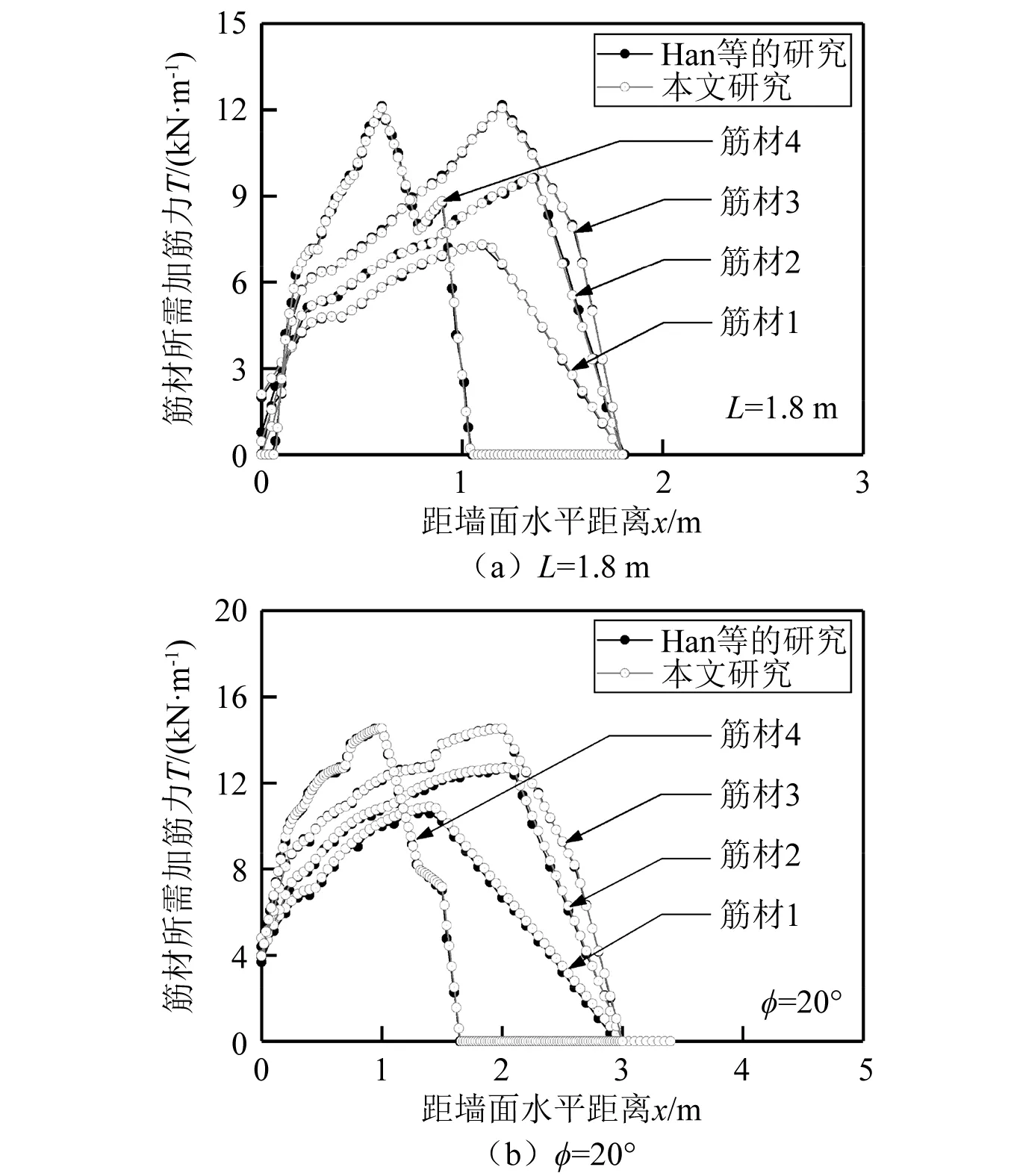
图4 静力状态结果对比Fig.4 Comparison of the calculated results with Han et al on static
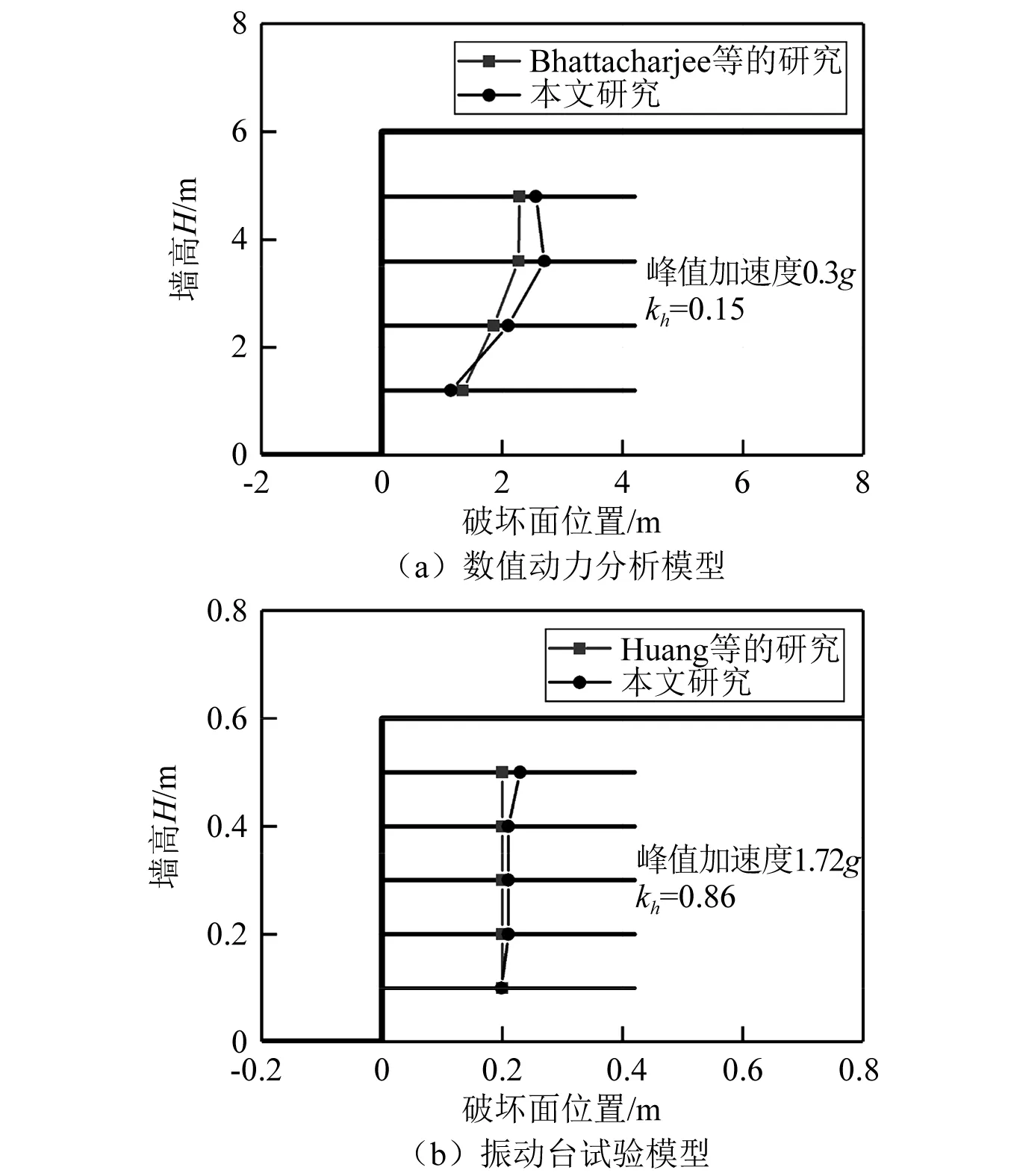
图5 地震加筋挡墙最危险滑动面位置结果对比Fig.5 Comparisons of the critical failure surfaces of seismic GRS walls
2 不同筋材布置方式下地震加筋土挡墙稳定所需加筋力分析
为了提高土工合成材料加筋土挡墙在地震作用下的稳定性,“美国规范”大都要求抗震设计时适当增加筋材布置长度,但筋材长度的增加对提高稳定性的影响有限,本文研究筋材布置方式对加筋土挡墙地震稳定性的影响以期为抗震设计提供新思路。本节将运用1.2节所述极限状态筋材加筋力逐层计算方法分析不同筋材布置方式(如单层加长、双层加长、短筋布置、变间距布置)对加筋土挡墙抗震稳定性的影响。本文土工合成材料加筋土挡墙的标准计算模型(Baseline),如图6所示,该模型墙高H=6 m,筋材长度L=4.2 m,筋材间距Sv=0.6 m,筋材共铺设10层,加筋区填土重度γ=20 kN/m3,内摩擦角φ=30°。

图6 加筋土挡墙标准计算模型Fig.6 Dimensions of the baseline case
2.1 局部筋材加长
美国联邦公路局加筋土结构设计指南(FHWA)建议在设计时将顶层筋材加长以避免挡墙顶部发生开裂,但是并未给出筋材加长位置。以标准计算模型为例,运用1.2节所述极限状态筋材加筋力逐层计算方法研究不同地震作用下(水平地震加速度系数kh分别取0,0.1,0.2和0.3)局部筋材加长(单层加长和双层加长)对土工合成材料加筋土挡墙稳定性的影响,结合相关规范综合考虑,设定筋材加长长度ΔL=5 m(在标准模型筋材长度的基础上加长5 m)。
不同单层筋材加长位置对加筋土挡墙地震稳定性的影响,如图7所示。从图7可知,位置1~位置10分别对应加长筋材1~筋材10,加筋土挡墙最大加筋力max(Tmax_l)与标准计算模型最大加筋力max(Tmax_b)的比值用来反映局部加长对加筋土挡墙地震稳定性的影响(max(Tmax)为各层筋材计算出加筋力的最大值),比值越小代表极限状态下稳定所需最大加筋力越小(在使用相同型号筋材的情况下会拥有更多的安全储备)。静力状态,筋材顶部加长可以有效减小挡墙稳定所需最大加筋力;随着地震强度增加,筋材所需最大加筋力减小趋势显著。最优筋材加长位置由顶部不断向挡墙中部移动,当kh=0.3时,筋材5所在位置进行局部加长最有效。

图7 单层加长对加筋土挡墙地震稳定性影响Fig.7 Effect of single reinforcement lengthening on the seismic stability of GRS walls
美国桥梁设计指南(AASHTO)建议加筋土挡墙抗震设计可适当增加挡墙顶部两层筋材的长度,但没有解释为何选择在顶层进行加长,该部分研究以标准计算模型为例分析不同位置双层筋材加长对加筋土挡墙稳定性的影响。双层加长意味着同时加长相邻两层筋材,加长长度均为ΔL=5 m。不同位置对应不同加长筋材层的组合,如图8所示。例如位置1对应加长筋材1和筋材2,位置2对应加长筋材2和筋材3,由上至下依次类推。

图8 双层加长对加筋土挡墙地震稳定性影响Fig.8 Effect of double reinforcement lengthening on the seismic stability of GRS walls
静力状态下,挡墙顶部双层加长对于减小最大加筋力效果最为显著,但随着地震强度的增加,最优加长位置同样表现出由挡墙顶部向挡墙中部移动的现象,当kh=0.3时,加长筋材5和筋材6的处理最为有效(对应图8的位置5)。可以发现,AASHTO标准建议的加长挡墙顶部两层筋材只有在静力状态下为最优方案,在地震状态下并不是合理选择。相较单层加长的方式,双层加长能够更多的减小挡墙所需最大加筋力,但无论采用哪种局部加长的布置方式,加长挡墙底部的筋材均无法提高加筋土挡墙地震稳定性。
2.2 短筋及变间距布置
短筋布置情况下加筋土挡墙静动力分析的试验和数值研究结果[38]表明,短筋布置对减小主筋拉力和墙面侧向变形有积极作用。由于边坡底部所受上覆压力较大,筋材的变间距布置方式常常在加筋土边坡设计中应用,通常加筋土边坡底部筋材间距要小于其上部,然而现行规范中加筋土挡墙的设计大都使用等间距的布置方式,对于变间距的筋材布置缺乏介绍说明。因此,该部分将研究不同长度的短筋布置以及变间距布置方式对加筋土挡墙地震稳定性的影响。在标准计算模型的基础上布置短筋(短筋共布置9层,各层筋材间距0.3 m),考虑3种短筋布置长度(Ls=1.0 m,Ls=1.5 m,Ls=2.0 m),如图9(a)所示;变间距筋材布置将挡墙分为上下两个区域,以筋材4所在位置作为分界点,上半区高H1=3.2 m,筋材间距Sv1=0.8 m,下半区高H2=2.8 m,筋材间距Sv2=0.4 m,如图9(b)所示。
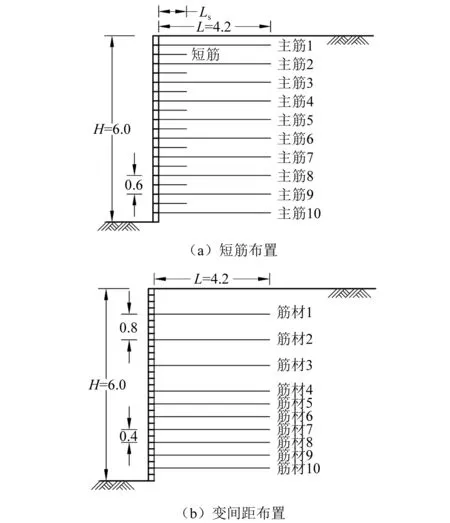
图9 短筋及变间距布置示意图 (m)Fig.9 Illustration of GRS wall (m)
静力状态下,短筋长度Ls=2.0m时挡墙所需最大加筋力减小最明显(最大约为25%),而在强震情况下(kh=0.3),变间距布置表现出比短筋布置更好的效果,如图10所示。随着地震作用的增强,短筋布置长度越长,挡墙最大加筋力减小越显著。当短筋长度Ls=1 m时,地震会导致最大加筋力明显增大且都超过标准模型对应的最大加筋力,说明该方案无法起到提高加筋土挡墙稳定性的效果。当短筋长度Ls=1.5 m时,地震情况下的最大加筋力大于静力情况,而Ls=2.0 m时出现相反的情况,这意味着短筋布置长度选择在1.5~2.0 m会有最好的效果。实际工程中尤其需要注意合理选择短筋布置长度,因不合理的长度设置将降低加筋土挡墙的地震稳定性,严重威胁工程安全。

图10 短筋布置及变间距对加筋土挡墙地震稳定性影响Fig.10 Effect of secondary reinforcement and variable spacing layout on the seismic stability of GRS walls
2.3 不同布置方式比较分析
为了更好地研究不同地震作用下筋材布置方式对土工合成材料加筋土挡墙稳定性的影响,定义最大加筋力减小率η为
(4)
式中: max(Tmax_b)为标准计算模型在不同地震作用下所需的最大加筋力; max(Tmax_l)为不同筋材布置方式对应地震作用下所需的最大加筋力。
选取不同地震作用下最优布置方案,如表1所示。绘制不同筋材布置情况下水平地震加速度系数kh与最大加筋力减小率η的关系图,如图11所示。静力状态下,短筋布置方式对于提高加筋土挡墙稳定性效果最好;随着地震作用增强,双层加长布置方式和变间距布置方式的优势逐渐显现,在强震作用下(kh=0.3)双层加长和变间距方式最大加筋力减小率可达约30%。
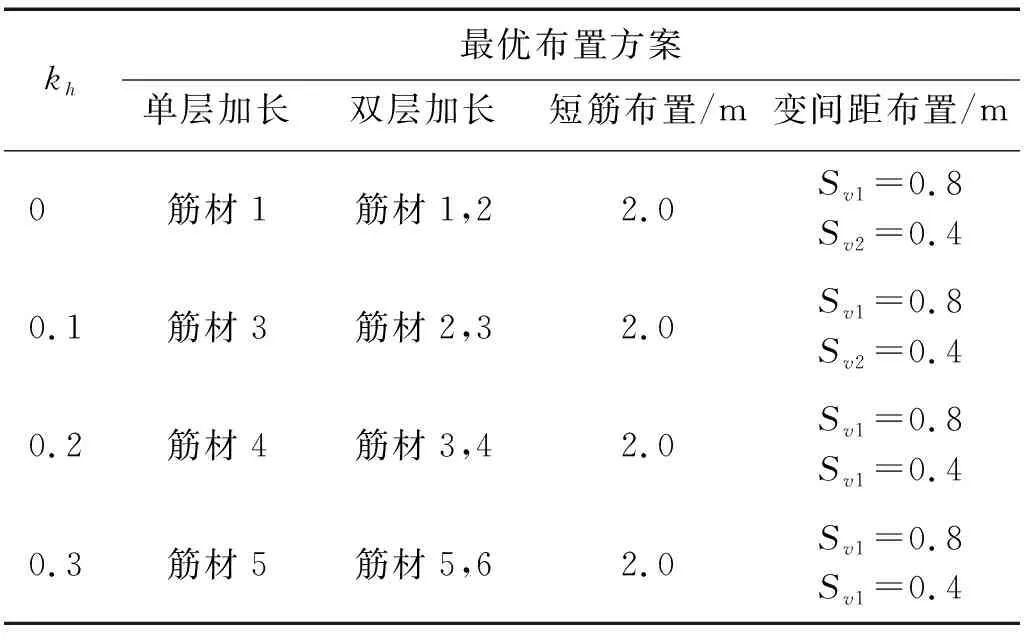
表1 不同地震作用下对应最优筋材布置方案Tab.1 Optimal layout of reinforcements subjected to different seismic loading

图11 不同地震作用下筋材布置对最大加筋力减小率的影响Fig.11 Effect of reinforcement layout on the η subjected to different seismic loading
1.2节所述筋材加筋力逐层计算方法可以获得不同地震作用下各筋材层加筋力Tmax和面板连接力To沿挡墙高度方向的分布情况,如图12所示。对于短筋布置方式,图12中结果为其主筋上的Tmax和To结果。可以发现,无论是在静力还是地震状态下,面板连接力To主要出现在挡墙的上部,而在挡墙中下部To结果都较小。需要注意的是,变间距方式产生的面板连接力To始终大于其他情况,而短筋布置则能够有效减小约50%的面板连接力To。静力状态下,最大加筋力Tmax沿高度方向分布都较为均匀,随着kh的增大,不同布置方式均出现Tmax下部大、上部小的特点。相对于标准计算模型的筋材布置方式,布置方式的改变均能够一定程度上减小各层筋材的Tmax,其中双层加长与变间距的布置方式在强震作用下(kh=0.3)效果最为显著,使得各层筋材的Tmax分布相对更均匀。

图12 不同地震和筋材布置方式对应筋材加筋力分布Fig.12 Different seismic and reinforcement layouts corresponding to the distribution of reinforcement loads
不同地震状态下,筋材布置方式对各筋材层最大加筋力位置的影响,如图13所示。静力状态下,不同布置方式在一定程度上均表现出直线破坏模式的规律,然而随着水平地震加速度系数的增大(尤其是强震状态下),不同筋材布置方式均表现出复合破坏的特点。
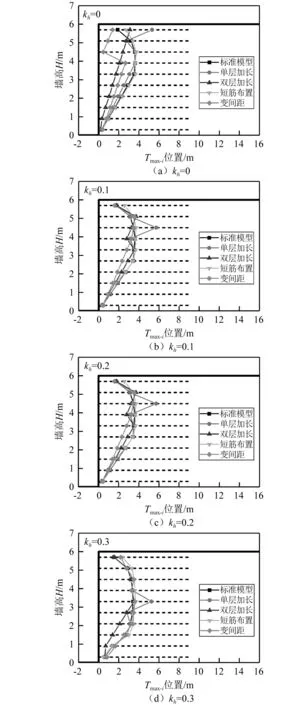
图13 不同地震和筋材布置方式对应各层最大加筋力位置Fig.13 Location of maximum reinforcement load for each layer corresponding to different seismic and reinforcement layouts
以强震工况(kh=0.3)为例,从最大加筋力max(Tmax)、最大面板连接力max(To)和筋材铺设总长度∑L3个方面对不同筋材布置方式进行综合分析,如表2所示。其中max(To_l)为不同布置方式所需最大面板连接力;max(To_b)为标准计算模型所需最大面板连接力;∑Ll代表不同布置方式所需筋材铺设总长度;∑Lb代表标准计算模型筋材铺设总长度。可以发现,局部加长方式(单层加长和双层加长)能够减少挡墙所需最大加筋力提高稳定性且筋材消耗量适中,但无法减小面板连接强度。短筋布置可以有效减小挡墙所需最大加筋力和面板连接力,但筋材消耗量最大。变间距布置同样可以减小最大加筋力且筋材消耗量最少,但会造成挡墙上部大间距区域面板连接力过大。因此,布置方式的选择需要根据工程实际情况(包括场地填筑空间、地震强度等)进行综合判断形成最优的抗震设计筋材布置方案。
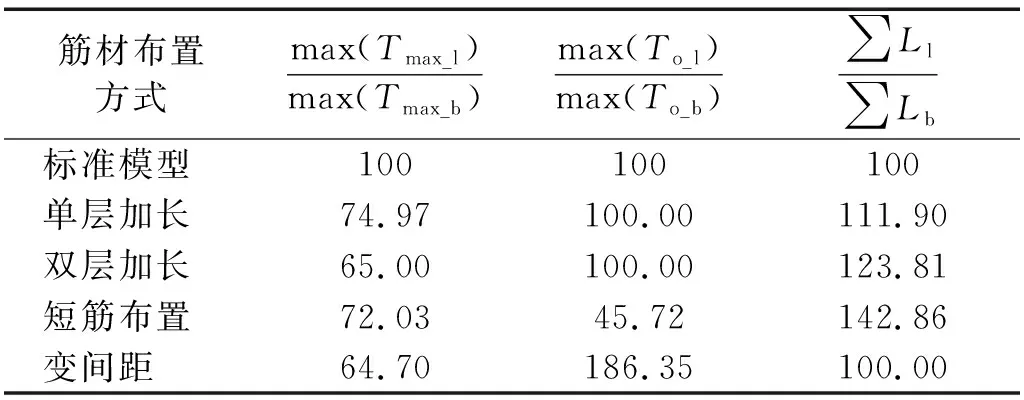
表2 不同筋材布置方案综合分析(kh=0.3)Tab.2 Comprehensive analysis of different reinforcement layout schemes (kh=0.3) 单位:%
3 结 论
本文基于极限平衡方法建立了地震加筋土挡墙稳定所需加筋力的计算方法,同时考虑筋材前、后端拔出破坏确定极限状态下筋材加筋力分布和面板连接力。运用该方法研究不同筋材布置方式(单层加长、双层加长、短筋布置、变间距布置)对水平地震作用下加筋土挡墙稳定性的影响规律,并获得了以下几点结论:
(1) 单/双层局部加长的筋材布置方式可以减少筋材所需的最大加筋力max(Tmax),且随着地震强度增加效果更为明显,最大减少约30%,筋材局部加长最优布置位置在挡墙中上部。
(2) 增加短筋布置长度可以显著减少最大加筋力(最大约25%),长度较小的短筋可能会导致最大加筋力增加,建议短筋长度选择在1.5~2.0 m。变间距布置方式可以减少最大加筋力约30%,但挡墙上部大间距区域的面板连接力To会有明显增加,此时需要注意加强挡墙上部面板与筋材的连接。
(3) 合理的筋材布置方式可以有效减小各层所需的加筋力,双层加长与变间距的布置方式在强震作用下效果最为显著,短筋布置方式则能够减少一半的面板连接力。
因此,在工程实践中需要选择合适的筋材布置方式进行加筋土挡墙抗震设计,如在场地受限的山区应考虑选择短筋布置或变间距布置方式,而在场地开阔地区建议选择双层加长方式提高加筋土挡墙抗震稳定性。
