加筋防护埋地管道静载特性的数值模拟与参数分析

李斌 于洪兴 肖成志

摘要 目前城市市政工程埋地管道的安全与防护是管理部门日益关注的重点，论文基于有限元数值模拟了静载作用下格栅加筋防护埋地管道的力学响应，综合对比研究了筋材埋深、长度和加筋层数等因素对埋地管道的力学与变形影响，数值计算结果表明：综合管道应力、变形和加载板极限承载力，确定了顶层筋材最佳埋深和长度分别为0.4倍加载板宽度和5倍管道外径;同等条件下，增加格栅加筋层数，地表加载板极限承载力显著增加，且在距中心点相同距离时，底层筋材的应力最大，顶层筋材的应力相对较小。

关 键 词 埋地管道;加筋防护;数值模拟;筋材;静载

中图分类号 TU431     文献标志码 A

Abstract Safety and sustainability of buried pipes has become more important due to the increase of the reported pipe failure incidents. Based on the numerical study in the paper， the performance of buried pipes reinforced with geogrids was investigated to understand the effect of embedment depth， length of geogrid and layers of reinforcement on the deformation characteristics of the buried pipes. The results indicated that the optimum burial depth and length of geogrid for the upper layer of geogrid were 0.4 times width of loading plate and 5 times outer diameter of pipe， respectively.  The bearing capacity at the surface above the pipe will increase with the increase of the number of layers of geogrid， and the stress of the bottom layer of geogrid is higher than the upper layer above buried pipes.

Key words buried pipes; reinforced protection; numerical simulation; reinforcement; static loading

0 引言

当前，遍布国内的油气埋地管道总长约85 000 km[1-2]，且未来相当长一段时间内管道总里程数将继续呈现上升趋势，导致埋地管道安全与防护面临着严峻的挑战，尤其是市政工程管道在大量城市基建工程面前，安全隐患日益增加[3-4]。因此，目前埋地管道安全防护成为学术界与工程界的关注热点。最初国内外倾向于通过控制管周土体性质或填埋工艺来实现管道保护，以达到管道上方变形模量与管道减载的效果（Dhar[5]、王晓谋[6]、周敏等[7]），但这类方法相对被动，后续一些学者尝试采用新型轻型材料达到减载的作用，如采用EPS和土工合成材料来实现加筋减载和防护的功能，其代表性的方法如Tupa[8]和Kawabata[9-10]等。进而，肖成志[11-12]等基于室内试验分析了格栅加筋防护管道的力学性能，并取得有益的结果。基于此，本文拟借助有限元数值方法，通过变参数来研究采用格栅加筋防护埋地管道时管道的静载力学响应，并综合对比分析筋材铺设参数如顶层筋材埋深和层数的影响，以此来确定铺设参数与加筋防护性能的相互影响。

1 基于筋材防护的埋地管道静力荷载响应的数值分析

1.1 埋地管道静载特性的数值模型

为了分析埋地管道采用格栅加筋防护的力学特性及筋材铺设参数的影响，这里选取管道埋深H=3D（D为埋地管道外径，mm），管周土体采用砂土，加载板宽度b=12 cm。基于平面应变分析管道力学性能，采用Abaqus软件数值计算模型高和宽分别为0.7 m和1.2 m，有限元网格划分如图1所示。计算时模型左右两侧边界限制水平位移，底部固定，并采用CPE4R平面应变缩减单元模拟土与管道，其优点是单元对位移的求解准确，且计算不易发生剪切自锁。另外，划分网格前需要对土体与管道分别进行分割处理。为了确保精度要求，土体与管道接触部分种子、土体和管道种子大小分别为7.5 mm、25 mm和8 mm。

模拟加载板加载时加筋防护埋地管道的力学与变形性能时，有限元模拟计算以加载板地基破坏或管道最大径向变形达到7.5%D时为终止条件。

1.2 管周土特性及有限元数值模型

1.3 埋地管道和防护筋材

埋地管道选取高密度聚乙烯（HDPE）材料，有限元数值分析中采用线弹性模型模拟管道。管道外径D = 110 mm，管壁厚t = 5.3 mm，密度[ρp]= 0.965 g/cm3，管材弹性模型取160 MPa，泊松比为0.4。

选取聚丙烯格栅加筋防护管道，筋材抗拉极限强度为30 kN/m，數值计算中筋材厚度为1 mm，抗拉模量为2 600 MPa，泊松比为0.3，密度为[ρg]= 0.95 g/cm3。数值分析时采用TRUSS单元模拟筋材，筋-土界面单元采用Constrain约束，并采用Embedded region命令将筋材嵌入到砂土区。

1.4 管-土相互作用及其数值模拟

管-土相互作用及其界面特性是数值分析的重点内容，这里采用面-面接触模拟管道与管周砂土的界面接触，并以管道所在面为主控面，管周砂土所在一侧为从属面，采用Abaqus中面-面离散法，以界面硬接触的法向模型罚刚度算法来定义管-土切向模型，基于管-砂土间界面特性试验确定其界面摩擦系数f为0.65。

2 有限元数值模拟结果分析

2.1 顶层格栅埋深对埋地管道性能的影响

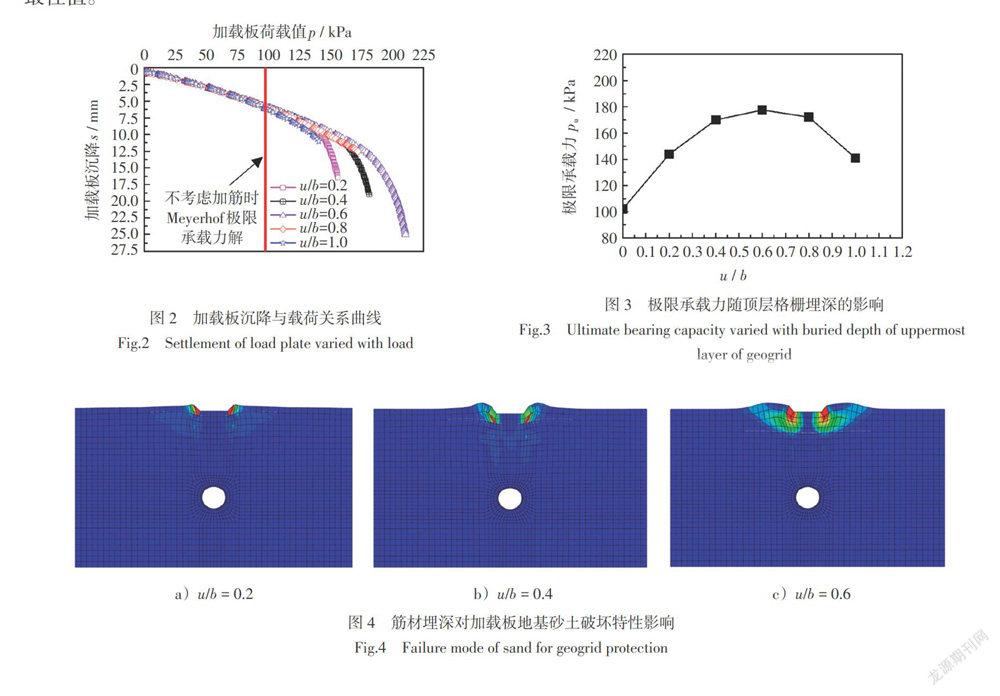
选取单层格栅即N = 1，针对管道埋深H = 3D，砂土相对密实度[Dr]= 60%，筋材长度L=5D时，分析单层筋材埋深u（或u/b）对埋地管道加筋防护性能的影响。图2和图3分别给出了沉降s随载荷P的变化曲线和地表加载板极限承载力随筋材埋深u的影响。由图2可知，当筋材埋深较大时即u/b = 0.8～1.0时，P—s曲线拐点不明显，极限承载力以管道径向变形达到允许变形;当u/b < 0.8时，P—s曲线拐点明显，即加载板极限承载力计算终止条件为地基破坏。另外，这里将不考虑加筋时采用Meyerhof极限承载力公式计算的地基承载力与不同u/b时进行对比，很明显铺设一层筋材后，尤其是u/b = 0.4～0.6时，加载板承载力明显提升。

由图3可知，与未铺设格栅（即u/b = 0）相比，在管道上方铺设筋材可显著增加极限承载力。而且管道上方加载板极限承载力总体上呈现先增加后减少的变化趋势，当格栅埋深u/b = 0.4时极限承载力达到最大值，而当u/b > 0.4即筋材距离地表越远时，加筋效果随埋深增加而被抑制，此时极限状态以加载板底部砂土地基破坏为主，且加载板极限承载力趋于和未加筋时相同。综合上述，顶层筋材埋深以（u/b）opt = 0.4为最佳值。

2.3 不同u/b时加载极限载荷下砂土破坏特性研究

这里选取u/b=0.2、0.4和0.6时，给出加载极限承载状态时加载板及管周土体等效塑性应变云图，如图4所示。由图可知，当筋材埋深较小如u/b=0.2时，加载板破坏以浅层土体破坏为主，极限承载力较低，随着筋材埋深增加，如u/b=0.4时，加载板底部砂土极限承载力所对应塑性应变区比u/b=0.2明显大，且筋材埋深越大，极限状态时塑性区范围越大，地表变形也相对较大且影响范围大，加载板两侧鼓起明显。另外，当铺设筋材加筋防护时，塑性应变区在筋材下方区域发展不显著，表明通过格栅加筋能有效抑制塑性区向地表以下更深处发展;当筋材埋深持续增加如u/b=0.6时，加载板底部塑性区总体上在筋材上方形成贯通带，且塑性区延伸到地表面，此时若继续增加筋材埋深，加载板底部砂土破坏模式与未铺设筋材相同。

2.4 不同u/b时格栅对埋地管道力学性能的影响

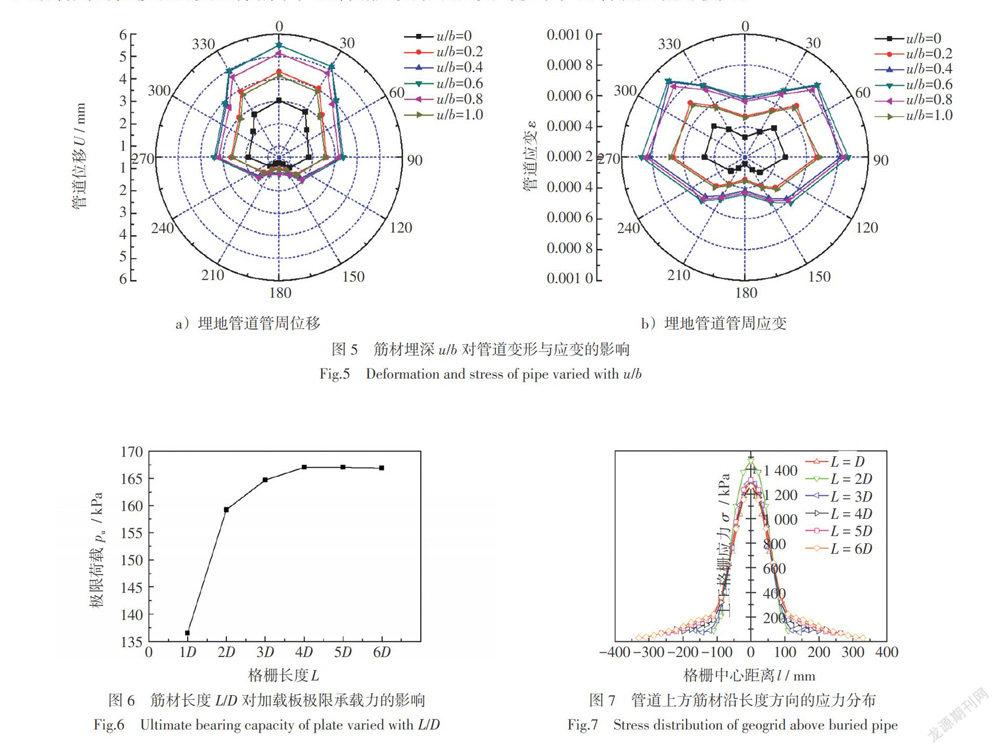
图5为极限载荷下，不同筋材埋深u/b时管道位移和应变沿管周的分布图。由图可知，不同u/b时管道位移和应变的分布模式不变，且当筋材埋深u/b= 0.4和0.6时，位移和应变较大，这是由于此时加载板极限承载力较大，而当u/b < 0.4或u/b > 0.6时，加载板极限承载力趋于相同，且与u/b = 0.4时相比较小，因此管道沿管周的位移和应变总体偏小，且管底处变形和应变均较小，而管顶处相对较大。

2.5 筋材长度L（L/D）对埋地管道性能的影响分析

基于上述确定的单层最佳埋深即（u/b）opt=0.4，选取H = 3D、[Dr]= 60%和N=1，通过改变格栅铺设长度L（或L/D）来分析筋材对埋地管道的性能影响，这里通过分析筋材对加载板极限承载力，以及筋材沿全长的应力分布规律等来确定其长度对管道性能的影响，并由此确定筋材最佳加载防护长度。

2.5.1 筋材长度L对加载板极限承载力的影响

选取单层筋材长度L = D、2D、3D、4D、5D和6D时，分析筋材长度对地表加载板极限承载力的影响，结果如图6所示。由图可知，当单根筋材铺设长度L从D增至2D时，加载板极限承载力显著增强，当筋材铺设长度由2D增至4D时，加载板极限承载力继续增加，但提升效果并不明显，且当L ≥ 4D时，管道上方加载板极限载荷趋于稳定，表明当筋材长度超过4D时，继续增加筋材铺设长度对提高管道上方加载板承载力无明显帮助。

2.5.2 筋材长度L对格栅应力分布规律的影响

图7为不同筋材长度L时加载板极限承载力作用下格栅应力沿全长的分布规律。由图可知，以加载板中心轴为对称轴，不同筋材铺设长度时筋材应力成对称分布，当筋材铺设长度L < 4D时，筋材沿全长受力，且对称轴中心处应力值最大，筋材在中心位置受载荷最大。当L ≥ 4D，如L = 5D和6D时，随着距中心距离增加，筋材应力逐渐减小，且当筋材长度超出4D，即距离格栅中心2D后，筋材应力渐趋于零。

综合图6和图7可知，当采用单层格栅加筋防护埋地管道时，格栅铺设最佳长度L以4D为最佳。

2.6 格栅铺设层数N对加筋防护管道性能的影响

基于上述结果，选取管道埋深H = 3D，筋材长度L = 4D，首层筋材埋深为u = 0.4b，分析管道上方铺设筋材层数N对管道力学与变形性能的影响。

2.6.1 筋材层数N对加载板极限承载力的影响

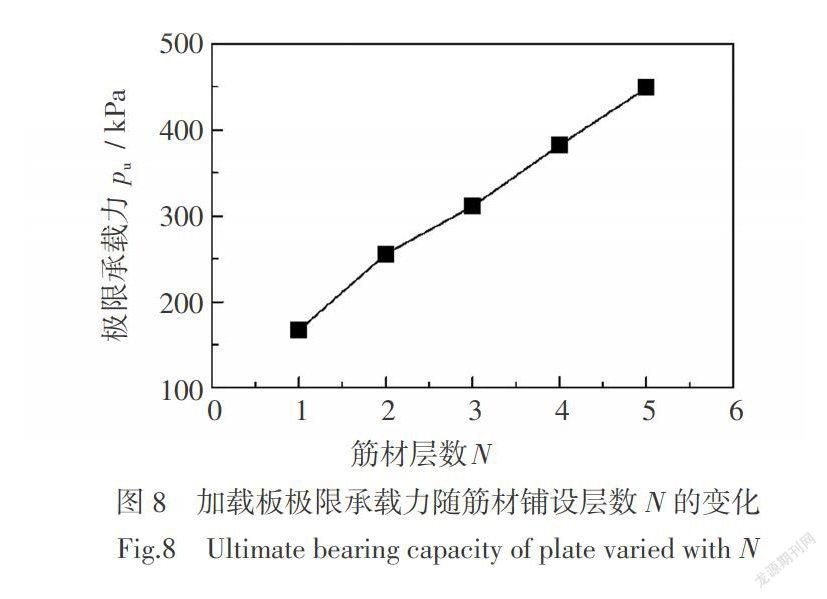
图8为筋材层数N对加载板极限承载能力的影响，由图可知，增加格栅层数对加载板极限承载力提高明显，考虑到增加格栅层数时，计算终止条件均以管道径向变形达到7.5%D为准，因此，管道上方加载板极限承载力随N增加而呈近似线性变化。

2.6.2 筋材层数N对埋地管道力学响应影响

图9为筋材层数N对埋地管道的力学与变形影响，由图9a）可知，增加筋材层数，埋地管道应力分布规律有变化，总体上，不同筋材层数时沿管周的应力最大值出现在上半腰附近，即45°～90°和270°～315°之間，管道水平径向以下即135°～225°和管顶附近应力较小。筋材层数不同时，沿管周应力值连线的变化趋势大致相同，随着筋材层数N增多，沿管道45°～315°与90°～270°范围内的连线斜率越来越大，即此时管道应力值变化越来越小，结果表明增加防护筋材的层数，对管道上部两腰部分的应力具有明显影响，其它部分的应力无明显影响。

此外，由图9b）可知，筋材层数N变化时，管道沿管周的位移主要集中在上半周，且管道最大位移约在0°～30°和330°～360°区域，且随着N增加，沿管周位移在30°～135°和225°～330°范围增长较快。对比无筋材即N = 0和筋材铺设层数N = 5时，发现沿管周位移分布图相对圆润，其因为主要是筋材层数不同时，对应的加载板极限承载力各自不同。

2.6.3 筋材层数N对埋地管道力学响应影响

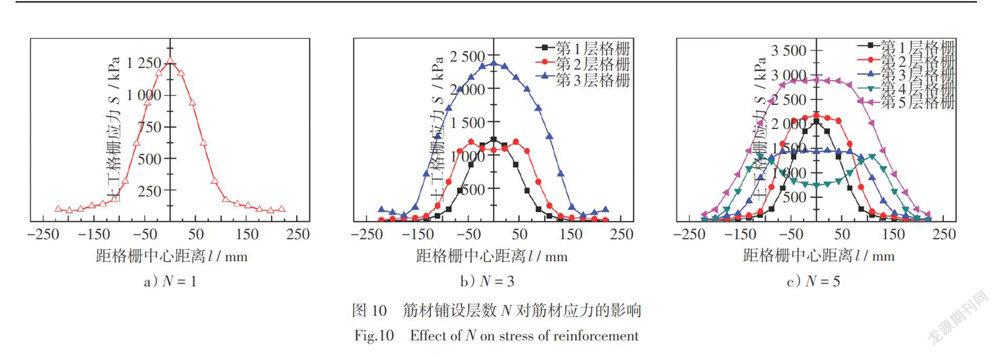
这里选取筋材层数N = 1、3和5时，分析极限荷载作用下筋材层数对筋材沿全长的分布规律，结果如图10所示。由图可知，当铺设多层筋材时，对应的加载板极限荷载下，距中心距离相同的點上，最下层格栅的应力最大，主要原因是当筋材层数增加时地基承载力提高，管顶及管顶附近土体变形明显，导致筋材应力增加明显。当N = 3时，顶层格栅应力分布规律与N = 1时相同，相比顶层和底层筋材，中间层筋材的应力在中心点附近比底层的筋材要小，且当N = 5时，具有相同的变化趋势，且格栅加筋层数越多，这种变化趋势越明显。另外，距中心点越远，格栅的应力逐渐在减小，并渐趋于相同。

3 结论

1）基于有限元数值方法，研究分析了埋地管道埋深为3D，管周土体相对密实度为60%时，格栅加筋防护埋地管道时的力学与变形性能，并确认了单层筋材最佳埋深和最佳长度分别为0.4b和5D。

2）埋地管道上方加载板极限承载能力随着筋材加筋层数增加而近似呈线性增加，且随筋材层数增加，顶层筋材沿全长应力变化规律相同，而中间层应力变化规律发生变化，且距中心点相同处，底层筋材应力普通要大于其它层，且随着距中心点距离的增加，格栅应力逐渐减小并最终趋于相同。

3）通过将土工合成材料引入到城市市政工程埋地管道的加筋减载和防护设计中，并针对筋材的铺设参数进行了量化分析，这为后续城市埋地管道的防护与施工具有重要的指导意义。

参考文献：

[1]    李国玉，马巍，王学力，等. 中俄原油管道漠大线运营后面临一些冻害问题及防治措施建议[J]. 岩土力学，2015，36（10）：2963-2973.

[2]    于红红，王德国，张华兵，等. 城镇燃气管道典型事故案例保护层分析[J]. 油气储运，2016，35（3）：254-258.

[3]    HEC D. European pipe line safety regulation and standards[R]. Technical Association of the European Gas Industry-Marcogaz，2008.

[4]    王玉梅，郭书平. 国外天然气管道事故分析[J]. 油气储运，2000，19（7）：5-10.

[5]    MARTSON A，ANDERSON A O. The theory of loads on pipes in ditches and tests of cement and clay drain tile and sewer pipe[R]. Bull 31 Iowa Engineering experiment Station，Ames. IA. 1913.

[6]    DHAR A S，MOORE I D，McGRATH T J. Two-dimensional analyses of thermoplastic culvert deformations and strains[J]. Journal of Geotechnical and Geoenvironmental Engineering，2004，130（2）：199-208.

[7]    王晓谋，顾安全. 上埋式管道垂直土压力的减荷措施[J]. 岩土工程学报，1990，12（3）：83-89.

[8]    周敏，杜延军，王非，等. 地层沉陷过程中埋地高密度聚乙烯（HDPE）管道力学行为研究[J]. 岩石力学与工程学报，2017，36（S2）：4177-4187.

[9]    TUPA N. The study of the application of soil reinforcement technique to minimize the consequences of explosions of buried pressurized pipes[D]. Brasilia：The University of Brasilia，2005.

[10]  周敏，杜延军，张亚军，等. 埋地HDPE管道施工过程中土拱效应变化特征研究[J]. 岩石力学与工程学报，2015，34（2）：414-424.

[11]  肖成志，杨亚欣，杨爱克，等. 静载作用下土工格栅加筋防护埋地管道力学性能实验研究[J]. 岩石力学与工程学报，2015，34（9）：1928-1937.

[12]  肖成志，王嘉勇，杨爱克. 静载作用下埋地管道数值模拟及其力学性能分析[J]. 防灾减灾工程学报，2018，38（1）：22-29，167.

[责任编辑 杨 屹]