颤振环境软金属碰撞滑动接触摩擦的分子动力学模拟
2023-01-11强宝宝佟瑞庭叶军权泽芬王静岩李士林
强宝宝,佟瑞庭,叶军,权泽芬,王静岩,李士林
(1.西北工业大学 机电学院,陕西 西安 710072;2.上海飞机设计研究院,上海 200436)
空间高真空、微重力是影响航天器运动机构摩擦和润滑性能的重要因素[1-3]。日本地球资源卫星一号(JERS-1)因空间环境微重力引发的空间颤振现象,雷达天线展开机构发生冷焊,导致卫星进入预定轨道后雷达天线无法正常展开[4]。美国伽利略号航天器因空间颤振现象引发高增益天线的定位销与V型槽销孔之间发生冷焊,造成高增益天线无法展开,导致航天器部分探测任务未完成[5]。国际空间站及哈勃望远镜等航天器的运动部件由于空间颤振环境的影响,反复发生摩擦润滑失效故障[4]。因此,空间摩擦学的研究得到越来越广泛的关注[6]。
空间环境中,传统的油、脂润滑剂易挥发、易爬移,导致机构润滑不足,而固体润滑剂因具有低蒸发率、低摩擦阻力等优异性能而得到广泛应用[7-10]。Ag、Au、Cu等软金属,由于低剪切强度,而且具有一定的抗压强度和韧性,作为固体润滑剂,能发挥其良好的减摩和润滑性能[11]。软金属固体润滑剂一般可通过离子镀、电镀、磁控溅射等方式附着于基材摩擦副表面,形成软金属涂层,实现减摩和润滑的作用[12]。Tong等[13]通过分子动力学模拟研究了高真空和微重力环境银薄膜的摩擦性能,结果表明空间颤振会导致银薄膜的摩擦力显著增加。袁志威等[14]通过磁控溅射技术在钛合金表面制备TaC和TaC-Ag涂层与氧化铝球进行对磨,结果表明,不同温度下TaC-Ag涂层的磨损率均低于TaC涂层,即加入Ag可提高涂层的耐磨性,因为Ag的添加使TaC晶粒细化,涂层的抗变形性能得以改善。吴耀佳等[15]研究表明,适量的软金属Ag与硬质涂层组合,可改善涂层的摩擦性能,提高硬质涂层的耐磨性能;但是添加过多的Ag会降低硬质涂层的耐腐蚀性。尹念等[12]模拟超高真空环境,研究了Au薄膜的摩擦性能,研究结果表明滑动速度较小时,界面之间有大量原子渗透,金属键持续断裂,摩擦力增大,同时磨损加剧。Tong等[16]通过分子动力学方法模拟真空微重力环境下的碰撞滑动接触摩擦行为,研究不同压头振幅、频率等对Au薄膜摩擦性能的影响,结果表明,当压头振动频率小于基体固有频率,压头频率的变化对平均摩擦力影响很小;当压头振动频率大于基体固有频率,提高压头的振动频率可以减小摩擦力。在固有频率下,压头振幅的变化对平均摩擦力和表面温度影响不大,在其他频率下,压头振幅对平均摩擦力和表面温度有明显影响。Lin等[17]通过模拟研究了Cu薄膜的摩擦性能,结果表明滑动速度较小时,随着滑动速度增大,摩擦力增大;当滑动速度较大时,Cu薄膜表面温度升高,表层软化,摩擦力减小。姚小飞等[18]在TC4钛合金表面通过硫酸盐镀铜技术制备Cu涂层,研究了Cu涂层对TC4钛合金基材摩擦磨损性能的影响。结果表明,覆有Cu涂层的TC4钛合金耐磨性优于无涂层的TC4钛合金基材;无涂层的TC4钛合金基材主要发生剥层磨损和黏着磨损,覆有Cu涂层的TC4钛合金会发生剥层磨损和疲劳磨损。Chen等[19]研究表明,与粗粒Cu相比,梯度纳米Cu涂层的磨损损失非常低,梯度纳米颗粒提高了涂层结构的稳定性,防止在高负荷下晶粒粗化,显著提高了Cu涂层的耐磨性。以上研究表明软金属具有一定的减摩和耐磨作用,但针对真空微重力环境导致的颤振现象对软金属摩擦性能的影响仍需进一步研究。
本文采用LAMMPS软件模拟研究真空微重力环境下软金属的摩擦性能。LAMMPS软件的模拟环境为真空环境,将微重力环境引起空间铰链机构的颤振简化为圆柱压头与基体之间的碰撞滑动接触运动,建立相应的分子动力学模型。针对空间铰链机构的运动特性,研究不同滑动速度、碰撞速度、压头半径对碰撞滑动接触摩擦性能的影响,并对比研究Ag、Au与Cu等不同软金属的摩擦性能。
1 模型建立
目前含间隙铰链机构在航天器上的应用非常广泛,如卫星天线展开机构(如图1所示)、太阳帆板驱动机构、机械臂、红外地平仪等姿态控制系统中的轴承组件[4],因此以含间隙铰链机构作为空间颤振环境碰撞滑动接触问题的研究对象。该机构可简化为由轴和轴承组成,将该模型沿轴向剖开,轴承简化为上、下基体,轴简化为圆柱压头,如图2所示。在微重力环境下,摩擦副受到轻微扰动时,会导致轴在轴承内发生无规则碰撞运动,引发颤振。将轴与轴承间的颤振等效为圆柱压头沿-z方向的碰撞,将轴的旋转运动等效为压头沿基体表面的水平滑动。因此,在空间微重力环境下,轴与轴承间的运动可等效为圆柱压头与基体间的滑动过程和碰撞过程的耦合运动,圆柱压头的滑动速度为V1,初始碰撞速度为V0,采用粗粒化分子动力学(CGMD)方法[20]研究碰撞滑动接触问题。
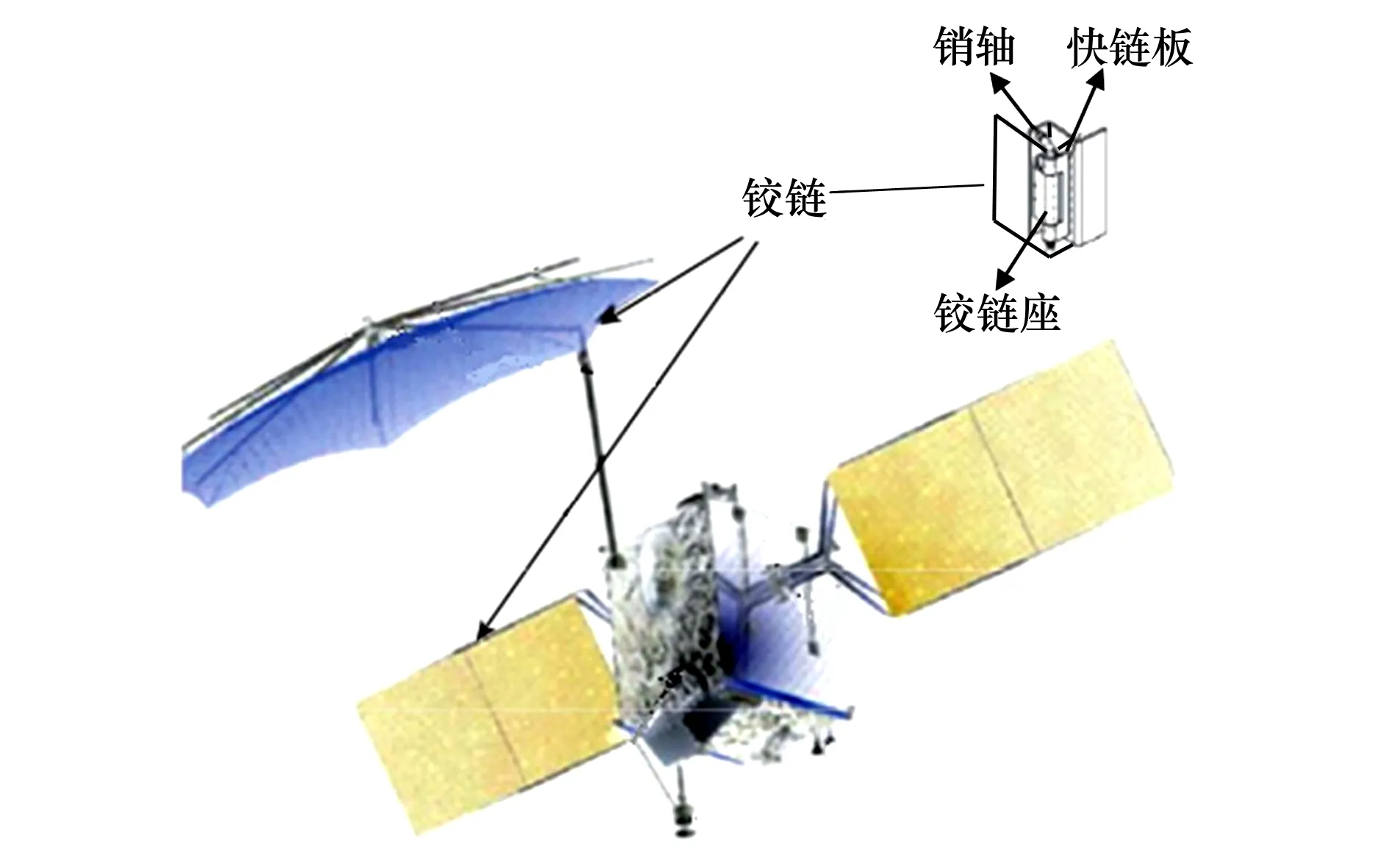
图1 卫星天线展开机构含间隙铰链图[4]
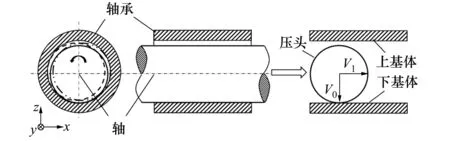
图2 含间隙铰链机构模型简化
以软金属Au为例,建立碰撞滑动接触问题的分子动力学模型。基体材料为单晶金,压头材料为单晶铁。模型在x,y,z方向的尺寸分别为114q,20q,100q(q为Au的晶格常数,q=0.408 nm),压头半径为35a(a为Fe的晶格常数,a=0.286 3 nm),上、下基体的尺寸均为114q×20q×18q。为节省模拟计算成本,将压头分为3个区域,区域1采用全原子(MD)形式,区域2采用CGMD1,区域3采用CGMD2(CGMD为粗粒化原子模型,CGMD1每个晶格由8个MD晶格组成,其晶格常数等于MD晶格常数的2倍,质量为MD粒子质量的8倍;CGMD2每个晶格由64个MD晶格组成,其晶格常数等于MD晶格常数的4倍,质量为MD粒子质量的64倍)。压头上、下各有9层晶格原子为MD形式,与之相邻的6层晶格原子为CGMD1形式,压头中间其余原子为CGMD2形式。基体由边界层原子、恒温层原子和牛顿层原子组成。以下基体为例,基体底部的3层原子为边界层,与边界层相邻的3层原子为恒温层,基体其余原子为牛顿层原子。基体的x方向和y方向采用周期性边界条件以减少尺寸效应的影响,在z方向采用固定边界条件。分子动力学模型如图3所示。

图3 碰撞滑动接触粗粒化分子动力学模型
模拟过程中,基体恒温层和牛顿层原子的运动遵循牛顿第二定律,以velocity-Verlet算法求解运动方程,设置时间步长为0.01 ps。压头发生运动前,采用NVT系综对系统进行弛豫,恒温层原子和牛顿层原子的弛豫温度为300 K,弛豫时间为50 ps,之后将系统转入NVE系综,弛豫50 ps至系统达到平衡。弛豫完成后,压头以碰撞速度V0(-z方向)、滑动速度V1(x方向)开始运动。
采用EAM势函数描述基体金属原子间的相互作用,采用Morse势函数描述Fe压头与基体金属原子间的相互作用。将压头等效为刚体,忽略压头内部原子间的相互作用。
关于EAM势,金属基体原子的总能量EM由(1)式计算
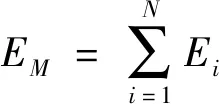
(1)
式中,原子i的能量Ei由(2)式计算

(2)
式中:Fi是原子i的嵌入能;ρi是由基体中所有其他原子产生的位于位置i的电子密度;φij是原子i和j之间的对势。
Morse势由(3)式计算
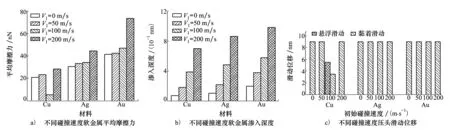
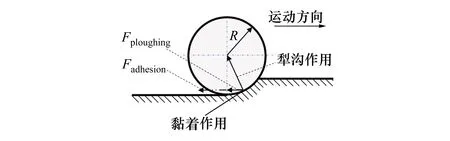
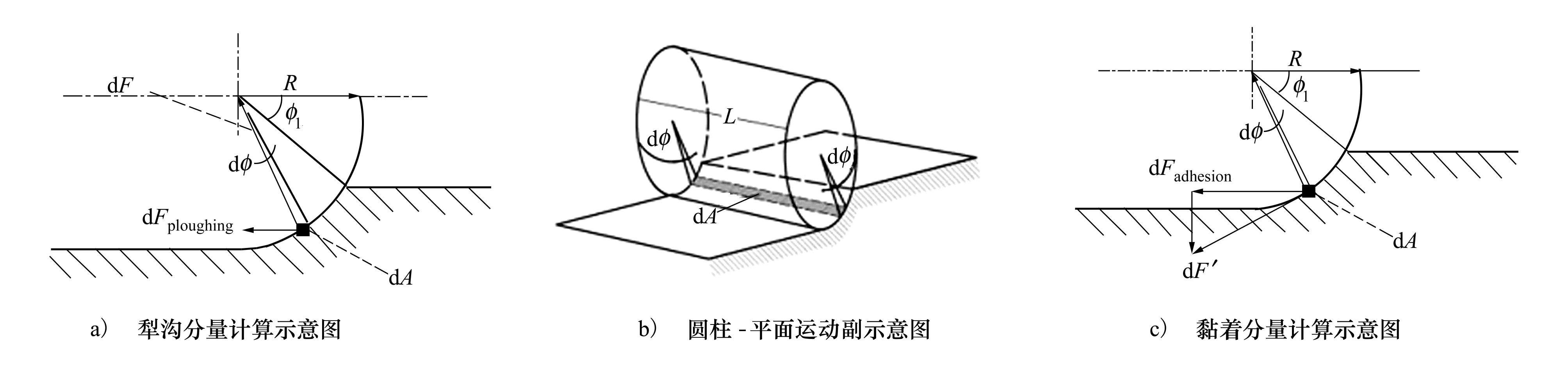
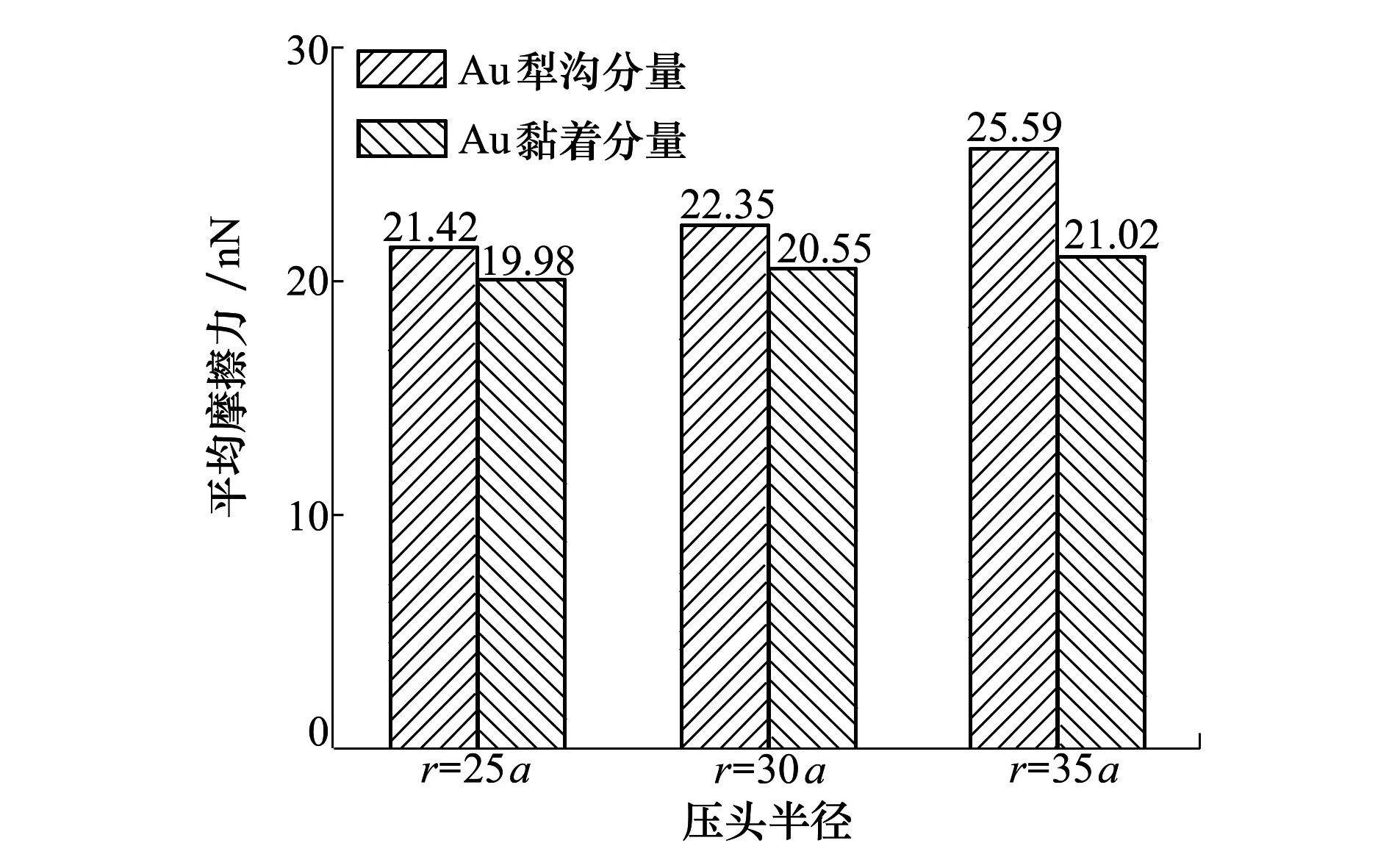
E=D0[e-2a(r-r0)-2e-a(r-r0)]r (3) 式中:D0是结合能;α是材料参数;r0是平衡距离;rc是截断半径;r是原子间距离。 根据Morse势混合规则[21],得到Fe-Cu、Fe-Ag、Fe-Au的势参数[22-23],如表1所示。 表1 Morse势参数 在颤振环境下,研究压头与基体之间不同滑动速度对摩擦性能的影响。压头在-z方向的初始碰撞速度为100 m/s,在x方向的滑动速度分别为10,20,50和100 m/s,滑动位移为9 nm。 基体材料为Au时,取前60 ps的压头碰撞速度曲线,分析压头与基体间的碰撞过程,如图4a)所示,与之相对应的法向力曲线如图4b)所示。图5是滑动速度为20 m/s、时间t=17 ps时基体的位错图。 如图4所示,压头的碰撞速度曲线以及法向力曲线在不同滑动速度下均呈现出类似的波动趋势,取滑动速度为20 m/s进行分析。压头与基体的碰撞过程分为3个阶段:碰撞阶段、回弹阶段和黏着分离阶段。在碰撞阶段中,如图4a)所示,t=13 ps时,压头碰撞速度V0=103.8 m/s,略大于压头的初始碰撞速度100 m/s。当压头与基体即将接触时,由于分子间相互作用力以吸引力为主(如图4b)所示,t=10~12 ps时压头与基体之间的相互作用力为负值,表现为相互吸引力),该吸引作用力与压头运动方向相同,对压头产生一定的加速作用,因此,压头碰撞速度呈现出微小增大。压头与基体接触之后,法向力逐渐增大,此时法向力阻碍压头向下运动,压头的碰撞速度逐渐减小。图4b)中,t=17 ps时法向力突然减小,之后继续增大,这是因为t=17 ps时,在压头作用下基体开始出现了位错(如图5所示,滑动速度为20 m/s、时间t=17 ps时基体发生了位错,红色线为基体位错线,绿色原子为FCC结构,黄色原子为其他结构),位错的产生使基体上累积的部分应变能得以释放,因此法向力会瞬时减小,而随着压头继续下压,法向力会逐渐增大。当碰撞速度减小至零时,压头处于基体的最大渗入深度处,此时法向力达到最大值,对应于图4b)中t=22 ps时刻,法向力达到最大为417.11 nN。此后,压头进入回弹阶段,压头开始向上运动,此时法向力作为压头回弹的动力,压头速度逐渐增大,法向力逐渐减小。当法向力趋于零时,压头达到回弹的最大速度(如图4a)~4b)中,t=31 ps时,法向力为零,压头达到回弹最大速度),此后压头进入黏着分离阶段。压头继续向上运动,由于黏着作用,压头与基体之间的作用力阻碍压头向上运动,因此压头的速度逐渐减小。由于压头与Au基体黏着作用较大,无法碰撞分离,此后压头会在z方向产生微小幅度振荡,并沿x方向继续匀速滑动。 此外,如图4a)所示,压头水平滑动速度分别为10,20,50和100 m/s,由于压头与Au基体的黏着作用较大,无法碰撞分离,压头在z方向振荡,压头的动能补偿振荡过程中黏着作用消耗的能量,因此碰撞速度会逐渐减小。随着滑动速度的增大,压头在z方向的碰撞速度衰减加快。滑动接触过程以黏性阻尼为主,滑动速度越大,压头在碰撞滑动过程中能量损耗越大,碰撞速度衰减越快。 图4 不同滑动速度压头的碰撞速度、法向力曲线图5 滑动速度为20 m/s、时间t=17 ps时基体位错图 不同滑动速度下,Au、Ag、Cu软金属的平均摩擦力、滑动位移如图6所示。图6a)中,随着滑动速度增加,压头与Cu基体的平均摩擦力先减小后增大,压头与Ag基体和Au基体的平均摩擦力逐渐增大。当滑动速度较小时,压头与Cu基体可碰撞分离,且悬浮滑动位移(悬浮滑动是指压头与基体碰撞分离后,压头会沿x方向继续滑动,此时压头处于悬浮状态)随滑动速度的增加先增大后减小(如图6b)所示,滑动速度为10,20和50 m/s时,悬浮滑动位移分别为2.1,5.52和2.45 nm)。由于悬浮滑动过程中,压头与基体间作用力较小,因此摩擦力呈现出先减小后增大趋势。当滑动速度较大时,压头与Cu基体始终处于黏着滑动接触状态,基体对压头黏着作用增强,因此摩擦力较大。压头与Ag基体和Au基体无法碰撞分离,始终处于黏着滑动状态,且随着滑动速度增大,黏着作用增强,摩擦力增大。 图6 不同滑动速度软金属的平均摩擦力、滑动位移 颤振环境下,不同碰撞速度会对压头与基体间的相互作用产生重要影响。选取-z方向的初始碰撞速度分别为0,50,100与200 m/s,压头在x方向的滑动速度为20 m/s,滑动位移为9 nm,研究碰撞速度对摩擦性能的影响。压头初始碰撞速度为0 m/s,即压头与基体不发生碰撞,系统弛豫完成后,压头在-z方向以10 m/s的速度靠近基体,以压头与基体之间即将产生相互作用力为临界点,认为压头与基体恰好接触,将压头的速度和作用力清零,再次对系统进行弛豫至平衡。然后压头以20 m/s的速度沿x方向滑动,模拟无碰撞滑动接触摩擦过程。 不同碰撞速度下,Au、Ag、Cu软金属的平均摩擦力、渗入深度和滑动位移如图7所示。图7a)中,随着碰撞速度的增大,压头与Cu基体间的平均摩擦力先增大后减小再增大,压头与Ag基体和Au基体间的摩擦力逐渐增大。当碰撞速度较小时,压头动能较小,与基体碰撞会导致部分能量损失,压头回弹的动能较小,无法克服Cu基体对压头的黏着作用,压头无法从基体碰撞分离,与Cu基体始终处于黏着滑动状态(如图7c)所示)。压头与基体不发生碰撞分离的情况下,碰撞速度越大,黏着作用越强,摩擦力越大,如图7a)中碰撞速度小于100 m/s的情况。随着碰撞速度继续增加,压头动能增大,压头回弹的动能较大,对于Cu基体,压头可碰撞分离,压头与基体之间的部分滑动处于悬浮滑动状态,黏着滑动位移较小(图7c)中碰撞速度为100 m/s时,压头与Cu基体悬浮滑动位移为5.52 nm,黏着滑动位移为3.48 nm),因此摩擦力较小。当碰撞速度更大(如碰撞速度为200 m/s)时,基体的渗入深度增大,接触面积增加,黏着作用增强,压头与Cu基体无法碰撞分离,始终处于黏着滑动状态,因此摩擦力较大;如图7b)中碰撞速度为200 m/s时,基体的渗入深度显著增加,且压头与Cu基体始终处于黏着滑动状态(如图7c)所示),导致摩擦力较大。压头与Ag基体和Au基体始终处于黏着滑动状态(如图7c)所示),初始碰撞速度越大,压头动能越大,基体渗入深度越深,接触面积越大,黏着作用越强,摩擦力也越大。 图7 不同碰撞速度软金属的平均摩擦力、渗入深度和滑动位移 压头半径对基体与压头的接触面积有重要影响,选取压头半径分别为25a,30a,35a,压头在x方向的滑动速度为20 m/s,在-z方向的初始碰撞速度为100 m/s,滑动位移为9 nm,研究压头半径对软金属摩擦性能的影响。 不同压头半径的平均摩擦力、Cu基体摩擦力曲线、滑动位移如图8所示。图8a)中,随着压头半径增大,压头与Cu基体间的平均摩擦力先增大后减小,压头与Ag基体和Au基体间的平均摩擦力逐渐增大。当压头半径分别为25a与30a时,压头与下基体Cu均可碰撞分离1次,最终与上基体Cu发生黏着滑动,且压头半径越大,动能越大,与下基体碰撞分离后回弹速度越大,悬浮滑动位移越小,黏着滑动位移越大(如图8c)所示),导致摩擦力越大。当压头半径为35a时,压头与Cu基体可碰撞分离2次,最终在下基体Cu上持续黏着滑动,压头悬浮滑动位移较长,黏着滑动位移较短,因此平均摩擦力较小。由于压头与Ag基体和Au基体未发生碰撞分离,始终处于黏着滑动状态(如图8c)所示),随着压头半径增大,动能增大,压头与基体的接触面积增加,摩擦力增大。 图8 不同压头半径的平均摩擦力、Cu基体摩擦力曲线和滑动位移 图8b)为不同半径压头与Cu基体之间的摩擦力曲线,t=31~84 ps时,压头与基体之间摩擦力为零,且半径越大,维持的时间越短。由于压头与Cu基体可碰撞分离,碰离后压头与基体处于悬浮滑动状态,因此摩擦力为零,且压头半径越大,动能越大,碰离后速度越大,z方向间隙相同时,所需时间越短。半径分别为25a与30a时,半径越大,摩擦力越大。因为半径越大,动能越大,压头与下基体碰离后的速度越大,与上基体的碰撞速度就越大,渗入深度越深,压头与上基体的接触面积越大,因此摩擦力越大。半径为35a时,压头与上、下基体均可碰撞分离,与上基体碰离后压头的速度较小,悬浮滑动时间较长(t=102~345 ps时,压头与基体处于悬浮滑动状态),黏着滑动位移较短,因此摩擦力较小。 此外,针对图8a)中不同压头半径时Au基体的平均摩擦力进行详细的理论分析探讨。根据经典摩擦学理论[24-25],摩擦力主要由两部分组成,一部分是由于摩擦副的界面剪切黏着作用形成的黏着分量,另一部分是由于材料变形阻碍压头向前运动的犁沟作用形成的犁沟分量,如图9所示,总摩擦力可以表示为 F=Fploughing+Fadhesion (4) 式中:Fploughing为犁沟分量;Fadhesion为黏着分量。 图9 圆柱-平面运动副摩擦力组成示意图 由图9可知,犁沟作用是基体沿垂直于接触面的方向对压头的作用力,摩擦力的犁沟分量为犁沟作用沿运动方向的分量。根据图10a)~10b)推导圆柱形压头与基体摩擦过程中摩擦力的犁沟分量,假设金属的屈服极限是各向同性的,则接触面积dA为 dA=RLdφ (5) 式中:R为圆柱形压头半径;L为圆柱形压头长度。 图10 圆柱-平面运动副摩擦力计算示意图 圆柱形压头的犁沟作用dF为 dF=δsdA (6) 式中,δs为金属屈服极限。 dF沿运动方向的分量为 dFploughing=dFcosφ=δsRLcosφdφ (7) 对dFploughing从φ1到π/2积分即可求得犁沟分量 Fploughing= (8) 如图10c)所示,圆柱形压头与基体间的黏着作用为 dF′=δcdA (9) 式中,δc为剪切强度。 dF′沿运动方向的分量为 dFadhesion=dF′sinφ=δcRLsinφdφ (10) 对dFadhesion从φ1到π/2积分即可求得黏着分量为 (11) 根据摩擦力的犁沟分量和黏着分量可知,当增大圆柱形压头半径时,摩擦力的犁沟分量和黏着分量都会增加。如图8a)中Au基体的平均摩擦力用摩擦分量表示如图11所示。随着压头半径增大,犁沟分量和黏着分量增大。由于压头半径增大时,动能增加,压头与基体的渗入深度增大,阻碍压头向前运动的犁沟作用增强,导致摩擦力的犁沟分量增大;同时压头与基体的接触面积增加,摩擦副剪切黏着作用增强,导致摩擦力的黏着分量增大。 图11 不同压头半径Au基体的摩擦分量 1) 当滑动速度较小时,压头与Cu基体发生碰撞分离,且悬浮滑动位移随滑动速度的增加表现为先增大后减小,因此摩擦力先减小后增大。当滑动速度较大时,压头与Cu基体始终处于黏着滑动状态,摩擦力较大。压头与Ag基体和Au基体始终处于黏着滑动状态,随着滑动速度增加,摩擦力增大。 2) 当碰撞速度较小时,压头与Cu基体始终处于黏着滑动状态,且碰撞速度越大,黏着作用越强,摩擦力越大。当碰撞速度增大时,压头与Cu基体之间的部分滑动处于悬浮滑动状态,摩擦力较小。继续增大碰撞速度,压头与Cu基体始终处于黏着滑动状态,压头在基体的渗入深度较大,接触面积增加,黏着作用增强,摩擦力较大。压头与Ag基体和Au基体始终处于黏着滑动状态,初始碰撞速度越高,压头动能越大。压头动能的增大导致基体渗入深度增大,进一步使接触面积增加,从而导致摩擦力增大。 3) 压头半径分别为25a,30a和35a时,压头在Cu基体均发生碰撞分离,压头与基体之间的部分滑动处于悬浮滑动状态,且半径为35a时,压头与Cu基体碰撞分离2次,悬浮滑动位移较长,黏着滑动位移较短,摩擦力较小。压头与Ag基体和Au基体始终处于黏着滑动状态,随着压头半径增大,动能增加,压头与基体的渗入深度增大,阻碍压头向前运动的犁沟作用增强,导致摩擦力的犁沟分量增大;同时压头与基体的接触面积增加,摩擦副剪切黏着作用增强,导致摩擦力的黏着分量增大。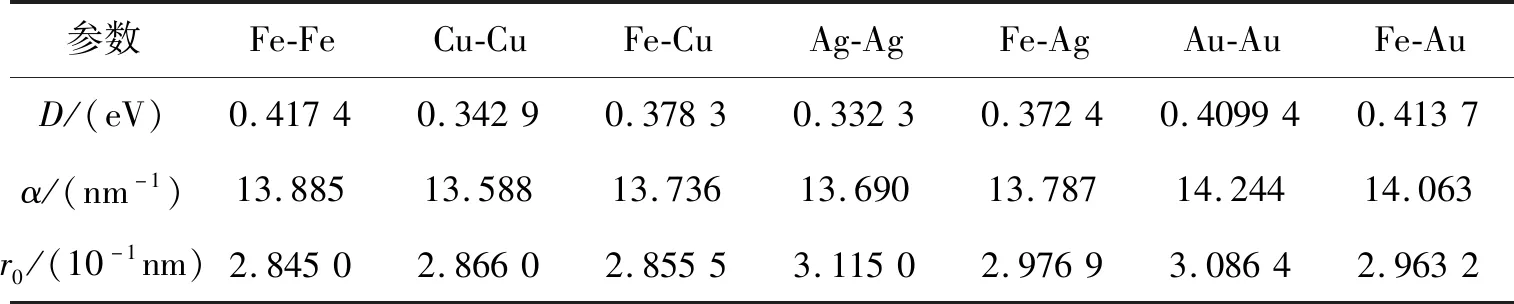
2 结果与分析
2.1 滑动速度的影响


2.2 碰撞速度的影响
2.3 压头半径的影响

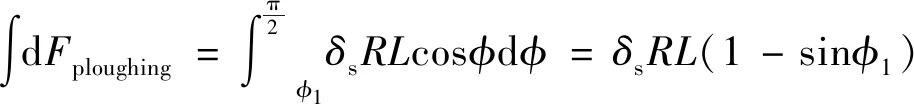
3 结 论
